- •36. Связь пределов последовательностей с арифметическими операциями.
- •37. Бесконечно малые, бесконечно большие последовательности.
- •38. Монотонные последовательности, число е
- •39. Понятие функции, области определения, значений. Способы задания функции.
- •40. Предел функции, теорема существования предела функции.
- •41. Бесконечно малые и бесконечно большие функции
- •42. Непрерывность функции в точке. Свойства непрерывных в точке функций.
- •1. Если функции и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .
- •2. Если функция непрерывна в точке и , то существует такая окрестность точки , в которой .
- •43. Точки разрыва функций.
- •44. Свойства функций, непрерывных на отрезке.
- •45. Производная функции. Её геометрический и механический смысл.
- •46. Производная суммы, произведения, частного.
- •47. Производная сложной, обратной функции. Производные сложных тригонометрических функций.
- •48. Функции, заданные параметрически и их дифференцирование.
- •49. Гиперболические функции. Их свойства и дифференцирование.
- •50. Дифференцируемость функции.
- •51. Дифференциал функции. Связь с производной, геометрический смысл.
- •52. Инвариартность формы дифференциала.
- •53. Производные высших порядков.
- •54. Формула Лейбница
- •55. Дифференциалы высших порядков.
- •56. Теоремы Ролля, Лагранжа, Коши.
- •57. Правило Лопиталя.
- •58. Формула Тейлора.
- •61. Исследование функций на экстремум при помощи производных высшего порядка.
- •62. Исследование функций на выпуклость и вогнутость. Точки перегиба функции.
- •63. Асимптоты кривых. Общая схема построения графиков функций.
42. Непрерывность функции в точке. Свойства непрерывных в точке функций.
Определение
1. Функция ![]() называется непрерывной
в точке
называется непрерывной
в точке ![]() ,
если она удовлетворяет следующим
условиям:
,
если она удовлетворяет следующим
условиям:
1)
определена в точке
,
т.е. существует ![]() ;
;
2)
имеет конечные односторонние пределы
функции при ![]() слева
и справа;
слева
и справа;
3) эти пределы равны значению функции в точке , т.е.
![]() .
.
Определение
2. Функция ![]() называется
непрерывной в точке
,
если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции:
называется
непрерывной в точке
,
если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции: ![]() .
.
Определения 1 и 2 равносильны.
Свойства функций, непрерывных в точке
1. Если функции и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .
2. Если функция непрерывна в точке и , то существует такая окрестность точки , в которой .
Доказательство
этого свойства основывается на том, что
при малых приращениях аргумента ![]() можно
получить как угодно малое приращение
функции
можно
получить как угодно малое приращение
функции ![]() в
окрестностях
в
окрестностях ![]() не
изменится.
не
изменится.
3. Если
функция![]() непрерывна
в точке
непрерывна
в точке ![]() ,
а функция
,
а функция ![]() непрерывна
в точке
,
то сложная функция
непрерывна
в точке
,
то сложная функция![]() непрерывна
в точке
.
Доказательство состоит в том, что малому
приращению аргумента
соответствует
как угодно малое приращение
непрерывна
в точке
.
Доказательство состоит в том, что малому
приращению аргумента
соответствует
как угодно малое приращение ![]() ,
приводящее в свою очередь к непрерывности
функции
к
как угодно малому
приращению
,
приводящее в свою очередь к непрерывности
функции
к
как угодно малому
приращению ![]() .
.
Свойство
можно записать: ![]() ,
,
Т.е. под знаком непрерывной функции можно переходить к пределу.
43. Точки разрыва функций.
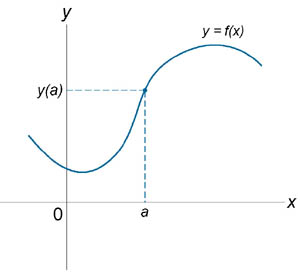
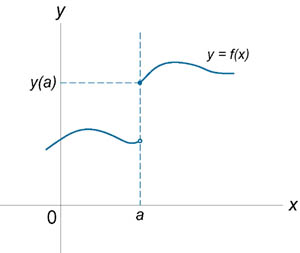
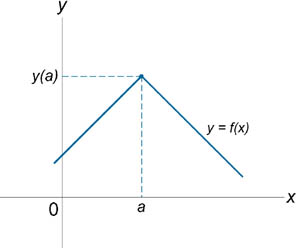
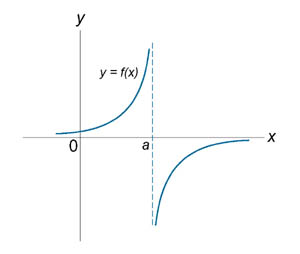
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
|
|
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
|
|
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
Рисунок 1. |
||
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
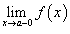 и
правосторонний предел
и
правосторонний предел  ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов![]() называется скачком
функции.
называется скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
44. Свойства функций, непрерывных на отрезке.
Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О[a, b] (рис.2).
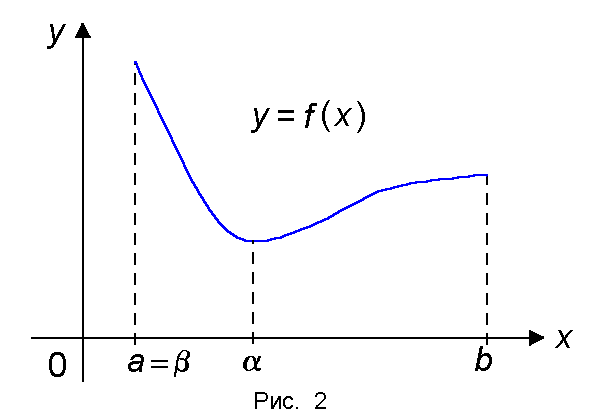
Наибольшее значение M обозначается символом maxx О [a, b] f(x), а наименьшее значение m — символом minx О [a, b] f(x).
Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.
Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).
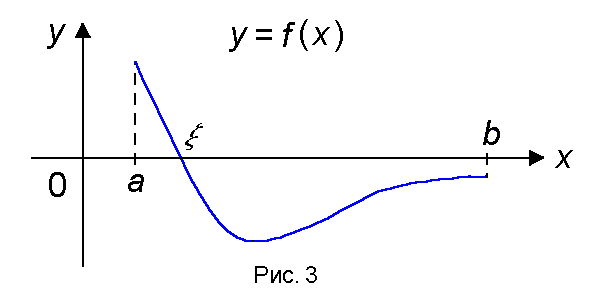
Замечание. На этой теореме основан метод приближенного решения уравнения
|
f(x) = 0, |
(1) |
называемый методом бисекции (дихотомии), или методом половинного деления.
Замечание. Метод неприменим для отыскания корней четной кратности.
Теорема 4 (Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b], то она принимает на (a,b) все промежуточные значения между f(a) и f(b).