57. Правило Лопиталя.
Первое правило Лопиталя
Пусть функции f (x) и g (x) непрерывны на отрезке [а, b] и дифференцируемы на интервале (а, b), и пусть g ' (x) ≠ 0 всюду в (а, b). Пусть, далее, известно, что f (а) = g (а) = 0. Тогда говорят, что отношение
при х → а +
0 представляет собой неопределённость
вида 
.
Теорема. Если
при указанных условиях
,
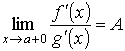то и
.
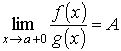Доказательство. Предположим, что ∞ < A < + ∞. Для заданного как угодно малого числа e > 0 выберем х0 так, чтобы в интервале (а, x0) выполнялось неравенство
.
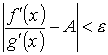Применим
теорему Коши к отрезку [а, x0],
Если х 
[а, x0],
то существует такая точка с
[а, x],
что
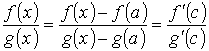
и, следовательно, для всех х [а, x0] справедливо неравенство
.
Это означает, что .
Второе правило Лопиталя
Пусть функции f (x) и g (x) непрерывны и дифференцируемы в интервале (a, b) (может быть, бесконечном) и g' (x) не обращается в нуль в (a, b). Пусть известно, что
.
Тогда
говорят, что отношение
при х → а +
0 представляет собой неопределённость
вида 
.
Теорема.
Если при указанных условиях
,
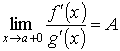то и
.
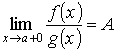Доказательство. Пусть А конечно. Для заданного как угодно малого числа ε > 0 выберем х0 так, чтобы в интервале (а, x0) выполнялось неравенство
.
Определим функцию D(x, x0) из условия
.
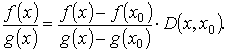Имеем
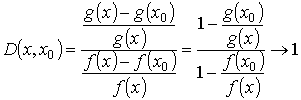
при x → a + 0. Применяя к отрезку [x, x0] теорему Коши, получаем, что некоторой точки с [x, x0]
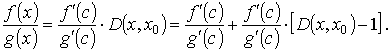
Отсюда для всех х, для которых | D( x, x0) - 1 | < ε, находим
Так как ε произвольно мало, то , что и требовалось доказать.
58. Формула Тейлора.
Пусть функция f ( x) имеет в точке а и некоторой её окрестности производные порядка n + 1. Пусть x ≠ a есть любое значение аргумента из указанной окрестности, тогда между точками а и х найдётся такая точка с, что справедлива формула
.
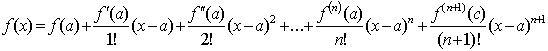Доказательство. Положим
, 
.
Функция F(x) имеет производные до порядка n + 1 вместе с функцией f (x). Функция G(x) имеет производные всех порядков, причём её производные положительны при х > a. Легко проверить, что
,
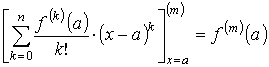и поэтому F (m)(а) = f (m)(а) – f (m)(а) = 0 при m = 0, 1, …, n. Так как G(m)(а) = 0 при m = 0, 1, …, n, то выполнены все условия обобщённой формулы Коши. При этом очевидно, что
F (n + 1)(х) = f (n + 1)(х), G(n + 1)(х) = (n + 1)!
Применение обобщённой формулы Коши к этим функциям приводит к соотношению
,
откуда и получается формула Тейлора с остаточным членом в форме Лагранжа
.
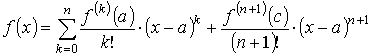Как видно, функция раскладывается на две части. Главная часть
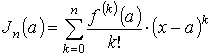
называется многочленом Тейлора порядка n. Второе слагаемое
называется остаточным членом функции в форме Лагранжа. Если в формуле Тейлора положить а = 0, то последняя обращается в формулу Маклорена
,
где с (0; х). Формула Тейлора позволяет функцию f (x), возможно, сложной природы, заменить приблизительно сравнительно простой функцией — многочленом.
Разложение некоторых элементарных функций по формуле Маклонена
,
,
,
,
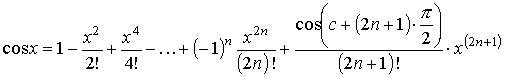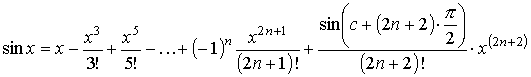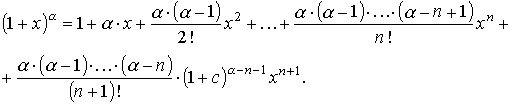
Формула Тейлора является эффективным средством для вычисления пределов функций, с которыми часто приходится иметь дело при исследовании функций.
59-60. Условия возрастания и убывания функций. Точки экстремума.
Достаточные условия возрастания и убывания функции в точке и на интервале
Теорема. Для того чтобы функция f (x), дифференцируемая в точке х0 Î (а, b), возрастала (убывала) в точке х0 , достаточно, чтобы f ' (x0) > 0 (f ' (x0) < 0). Доказательство. Так как по условию f (x) дифференцируема в точке х0 Î (а ,b), то существует предел
.
В достаточно малой окрестности точки х0 имеем
,
где sign A означает "знак выражения А". Для случая f ' (x0) > 0 имеем sign f ' (x0) = + 1, поэтому
sign (f ( x0 + h) − f ( x0)) = sign (h).
Откуда следует f (x0 − h) < f (x0) < f (x0 + h), что означает возрастание функции в точке.
Необходимые условия возрастания и убывания функции в точке и на интервале
Теорема. Для того чтобы функция f (x), дифференцируемая в точке х0 Î (а, b), возрастала (убывала) в точке x0, необходимо, чтобы её производная в точкех0 была неотрицательной f ' (x0) ≥ 0 (неположительной f ' (x0) ≤ 0). Доказательство. Пусть функция f (x) возрастает в точке х0 Î (а, b) и справедливы неравенства
f (x0 − h) < f (x0) < f (x0 + h)
В этом случае для положительного приращения h имеем
и 
.
Выполняя предельный переход в неравенствах, получим
.
Аналогично
.
Так как функция имеет производную в точке, то
,
что и требовалось доказать. Определение. Функция f (x) называется строго возрастающей (убывающей) на отрезке [а, b], если для любых значений аргументов из этого отрезка большему значению аргумента соответствует строго большее (меньшее) значение функции. Как следствие теоремы Лагранжа можно сформулировать теорему. Теорема. Если функция f (x) определена на отрезке [а, b], дифференцируема в точках х Î (а, b) и
f ' (x) > 0, ( f ' (x) < 0),
то функция f (x) возрастает (убывает) на отрезке [а, b ]. Доказательство. Применим теорему о конечных приращениях для двух произвольных точек х1 < х2 Î [а, b]
f (x2) − f (x1) = f ' (c)·( x2 − x1),
где с Î ( x1 ; x2). Из этого соотношения следует
sign ( f (x2 ) − f ( x1 ) ) = sign f ' ( c)
В случае f ' (x) > 0 для всех х Î (а, b) имеем f (x2) > f (x1) , и большему значению аргумента соответствует большее значение функции. Что свидетельствует о возрастании функции.
Точки экстремума
Точка x0 называется точкой строгого локального максимума (минимума) функции f (x), если для всех значений аргумента из некоторой достаточно малой δ -окрестности точки х0 выполняется неравенство
f (x) < f (x0) ( f ( x) > f ( x0 ) )
при х ≠ x0. Локальный максимум и локальный минимум объединяются общим названием экстремум. Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство f ( x) < f ( x0) ( f (x) > f ( x0 )) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки x0. Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то другого локального минимума. В точках экстремума приращение функции имеет определённый знак. Если Δ f = f ( x0 + h ) − f ( x0) ≥ 0 для достаточно малых значений h, то точка х0 является точкой локального минимума. Если Δ f = f ( x0 + h ) − f (x0) ≤ 0 для достаточно малых значений h, то точка х0 является точкой локального максимума. Точки экстремума это точки графика функции, которые отделяют участки определённой монотонности друг от друга. Ниже приведены виды точек экстремумов. В первых двух функция определена и производная существует, такие точки называются стационарными. Функция в точках экстремума определена, однако производной в точке экстремума может не существовать.
Необходимое условие экстремума
Теорема. Если х0 — точка экстремума функции f (x), то либо в этой точке производная обращается в нуль f ' (x0) = 0 (в стационарных точках), либо в этих точках производная не существует (в угловых точках). Доказательство. Рассмотрим разложение функции в окрестности точки х0 в ряд Тейлора с остаточным членом в форме Пеано
Δ f (x) = f ' (x0)·Δ x + o(Δ x).
Так как остаточный член является бесконечно малой величиной относительно приращения аргумента, то
sign Δ f (x) = sign f ' (x0)·sign Δ x,
и знак приращения функции зависит от знака приращения аргумента sign (Δ x). Что недопустимо для точек экстремума. Следовательно производная функции в точке х0 или равна нулю, или не должна существовать.
Достаточное условие экстремума
Теорема. Пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х1, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х1. Если при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то при х = х1 функция имеет локальный максимум. Если же при переходе слева направо через эту точку х1 производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум. Комментарий. Если в достаточно малой окрестности точки х1 справедливо f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1, то в точке х1 функция имеет максимум; если f' (x) < 0 при х < x1, f ' (x) > 0 при х > x1, то в точке х1 функция имеет минимум. Доказательство. Пусть при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то есть для всех х, достаточно близких к х1, имеем f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1. Применяя теорему Лагранжа к разности f (x) − f ( x1), получим
f ( x ) − f ( x1 ) = f ' ( c )·( x − x1 ).
где с лежит между точками х и х1. По условию теоремы
sign f ' ( c ) = − sign ( x − x1 ),
поэтому в произвольно малой окрестности точки х1 имеем
f ( x ) < f ( x1 ).
В этом случае точка х1 есть точка локального максимума, что и требовалось доказать.