- •4 Сравнение бесконечно малых функций
- •6.Непрерывность функции в точке
- •13.Основные теоремы дифференциального исчисления. Теоремы Ролля, Лагранжа и Коши.
- •15. Достаточные условия экстремума функции одной переменной. Экстремум функции – это ее локальный максимум или минимум.
- •16.Необходимое условие экстремума функции одной переменной.
- •17. Нахождение асимптот графика функции одной переменной.
13.Основные теоремы дифференциального исчисления. Теоремы Ролля, Лагранжа и Коши.
Теорема Ролля
Пусть
функция![]() .
Тогда
.
Тогда![]() ■
■
□ Из
условия![]() следует
по свойству 10
непрерывных на
следует
по свойству 10
непрерывных на![]() функций,
что
функций,
что![]() .
.
Существует две возможности:
1)
![]() ;
;
2)
![]() в
силу
в
силу![]() .
.
Пусть![]() ,
тогда согласно теореме Ферма
,
тогда согласно теореме Ферма![]() .
.
Данная теорема обладает таким же геометрическим истолкованием, что и теорема Ферма.
Теорема Лагранжа
Пусть
функция![]() .
Тогда
.
Тогда![]() ■
■
□ Введём
на
вспомогательную
функцию![]() ,
для которой верны условия теоремы
Ролля:
,
для которой верны условия теоремы
Ролля:![]() или
или![]() .
.
Следовательно![]() .
.
Солгасно
т. Ролля![]() :
:
![]() ◙
◙
Геометрическое
истолкование теоремы Лагранжа. Строим
график функции
(рис.
10.2),
![]() .
Угловой коэффициент касательной в т.
.
Угловой коэффициент касательной в т.
![]() .
Следовательно, на графике функции
.
Следовательно, на графике функции![]() .
.
Теорема Коши
Пусть
функции
![]() .
Тогда
.
Тогда![]() ■
■
В
формуле![]() .
В противном случае согласно теореме
Ролля
.
В противном случае согласно теореме
Ролля![]() .
.
□ Введём
![]() .
Подберём такое
.
Подберём такое![]() ,
чтобы
,
чтобы![]()
Тогда![]() .
По теореме Ролля
.
По теореме Ролля
![]() .
.
Теорема
Коши является обобщением теоремы
Лагранжа, где
![]() .
.
14.
Правило Лопиталя. Правило
Бернулли-Лопита́ля —
метод нахождения пределов
функций,
раскрывающий
неопределённости
вида 0 / 0 и
![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
Условия:
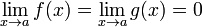 или
или
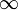 ;
;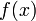 и
и
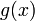 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности
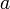 ;
;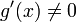 в
проколотой окрестности
;
в
проколотой окрестности
;существует
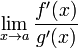 ,
,
тогда
существует
![]() .
.
Пределы также могут быть односторонними.
15. Достаточные условия экстремума функции одной переменной. Экстремум функции – это ее локальный максимум или минимум.
1. Случай функции одной переменной. Заметим, что максимум или минимум дифференцируемой функции может находиться лишь в ее критической точке (необходимое условие экстремума).
Пусть х0 – критическая (стационарная) точка функции y = f(x) (т.е. внутренняя точка области ее определения, в которой производная равна нулю). Тогда можно сформулировать следующие достаточные условия существования экстремума в этой точке:
а) Пусть функция дифференцируема в некоторой окрестности U точки х0, не содержащей других критических точек. Тогда:
если при переходе через точку х0 производная f ' меняет свой знак с плюса на минус, х0 – точка (локального) максимума функции;
если при переходе через точку х0 производная меняет свой знак с минуса на плюс, х0 – точка (локального) минимума функции;
если при переходе через точку х0 производная не меняет свой знак, в точке х0 нет экстремума.
б) Пусть в точке х0 существует вторая производная функции f, f ''(x0), не равная нулю. Тогда:
если f’’(x0) > 0, х0 – точка (локального) минимума функции;
если f’’(x0) < 0, х0 – точка (локального) максимума функции.
16.Необходимое условие экстремума функции одной переменной.
Определение
1.
Точка
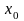 называется точкой локального
максимума
(минимума),
а значение функции в ней – локальным
максимумом
(локальным
минимумом)
функции
называется точкой локального
максимума
(минимума),
а значение функции в ней – локальным
максимумом
(локальным
минимумом)
функции
 ,
если существует
,
если существует
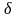 -окрестность
-окрестность
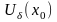 точки
такая, что в любой точке
точки
такая, что в любой точке
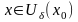 имеем
имеем
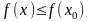 (соответственно,
(соответственно,
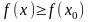 ).
).
Определение
2.
Точка
называется точкой строгого
локального максимума
(минимума),
а значение функции в ней – строгим
локальным максимумом
(локальным
минимумом)
функции
,
если существует
-окрестность
точки
такая, что в любой точке
имеем
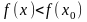 (соответственно,
(соответственно,
 ).
).
Определение 3. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них – локальными экстремумами функции.
Теорема
1.
(необходимое
условие локального экстремума функции).
Если
функция
 дифференцируема в точке
и имеет в этой точке локальный экстремум,
то
дифференцируема в точке
и имеет в этой точке локальный экстремум,
то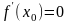 .
.
Доказательство.
По
условию теоремы существует конечная
производная
 .
Так как функция
имеет в точке
локальный экстремум, то она не может в
этой точке
ни возрастать, ни убывать. Значит,
производная
не
может быть ни положительной, ни
отрицательной. Тем самым доказано, что
.
■
.
Так как функция
имеет в точке
локальный экстремум, то она не может в
этой точке
ни возрастать, ни убывать. Значит,
производная
не
может быть ни положительной, ни
отрицательной. Тем самым доказано, что
.
■
Теорема 1 имеет очень простой геометрический смысл: она утверждает, что если в той точке кривой , в которой достигается локальный экстремум, существует касательная к этой кривой, то эта касательная обязательно параллельна оси Ох
Определение
4. Точки,
которых производная
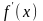 функции
обращается в нуль, называются стационарными
точками функции
функции
обращается в нуль, называются стационарными
точками функции
 и
и
 и
и
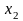 ).
).
Определение 5. Точки, которых производная функции не существует, но в них определена, называются критическими точками функции