
- •1.1 Понятие о моделировании.
- •1.2 Системы массового обслуживания
- •2.1. Виды моделирования.
- •2.2Моделирование простейшей одноканальной системы смо
- •3.1. Математическое моделирование. Источники ошибок. Необходимость тестирования.
- •3.2 Простейший поток событий
- •4.1 Необходимость тестирования компьютерных моделей.
- •4.2. Замкнутые смо
- •5.1. Сравнение некоторых пакетов, расчетов и моделирований.
- •5.2. Открытая смо
- •6.1 Примеры задач приводящих к необходимости решения дифференциальных уравнений.
- •6.2 Понятие о конкурирующих стратегиях. Пример алгоритма для выбора рациональной стратегии.
- •7.1 Сведение произвольной системы оду произвольного порядка к системе оду 1-го порядка.
- •7.2 Приближение инженерных данных. Виды приближений.
- •Поточечное среднеквадратическое приближение.
- •Непрерывное приближение в среднеквадратичном смысле.
- •Равномерное приближение.
- •8.1 Примеры сведения дифференциальных уравнений и их систем произвольного порядка к системе оду 1-го порядка в канонической форме Коши.
- •8.2. Интерполирование. Аппроксимация методом наименьших квадратов. Равномерное приближение. Поточечная аппроксимация табличных данных по методу наименьших квадратов.
- •9.1 Пример решения задачи о колебаниях одно массовой системы на основе использования встроенной процедуры Rkadapt.
- •9.2 Разложение аппроксиматора по системе базисных функций. Сведение задачи аппроксимации к системе лау.
- •10.1 Математическое моделирование механических колебательных систем со сосредоточенными параметрами .Системы с распределенными и сосредоточенными параметрами.
- •Пример использования разложения аппроксиматора по базисным функциям в виде мономов.
- •11.1 Методика получения модели механических колебательной системы сосредоточенными параметрами на основе уравнений Лагранжа 2-ого рода
- •11.2Интерполирование, алгебраическое интерполирование, классический подход
- •12.1 Пример получения математической модели для двух массовой колебательной системы
- •12.2 Интерполирование на основе формулы Лагранжа
- •13.1 Математическая модель колебательной системы с вращательными степенями свободы
- •13.2 Пример документа MathCad реализующий поточечную среднеквадратичную аппроксимацию
- •14.1 Некоторые примеры MathCad для решения различных задач
- •14.2 Остаточный член формулы Лагранжа, пример оценки точности интерполирования с использованием остаточного члена
- •15.1 Пошаговые методы решения задачи Коши
- •15.2 О наилучшем выборе узлов интерполирования
- •16.1 Метод Эйлера для решения задачи Коши, реализация этого метод в среде MathCad
- •16.2 Тригонометрическое интерполирование
- •17.1 Модификация метода Эйлера для решения задачи Коши
- •17.2 Использование интерполирования при решении различных задач и реализация в среде MathCad
- •18.1 Метод типа Рунге-Кутта для решения задачи Коши
- •18.2 Использование встроенных функций для линейной аппроксимации по методу наименьших квадратов
- •19.1 Связь модифицированных методов Эйлера и методов Рунге-Кута второго порядка для решения задачи Коши
- •19.2 Понятие о сплайнах
- •20.1 Метод Рунге-Кута 4-ого порядка для решения задачи Коши формулы метода и их реализация в среде MathCad
- •20.2 Определение сплайна. Дефект сплайна, пример линейного сплйна
- •21.1.Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.
- •21.2 Кубический сплайн дефекта 2 (или сплайн Эрмита).
- •22.1 Метод стрельбы
- •22.2 Кубические сплайны дефекта 1
- •23.1 Использование случайных величин при моделировании различных явлений и процессов
- •23.2 Алгоритм «прогонка» для решения системы линейных уравнений с диагональным преобладанием.
- •24.1 Задача Бюффона как пример использования случайных величин при решении детерминированной задачи.
- •24.2 Пример использования сплайна для приближенного интегрирования функции
- •25.2 Использование параметрических сплайнов для интерполирования кривых
- •26.1 Пример реализации метода типа Монте-Карло в среде Mathcad для вычисления площади произвольной фигуры
- •26.2 Параметрический Эрмитов кубический сплайн.
- •27.1 Основные виды моделирования их преимущества и недостатки
- •27.2 Рациональные сплайны.
- •28.1 Декомпозиция и диакоптика
- •28.2Параметрический рациональный сплайн.
- •29.1 Понятие о компонентных и топологических уравнениях
- •Механическая поступательная система.
- •29.2 О выборе узлов сетки при интерполировании различными сплайнами
- •30.1 Примеры получения эквивалентах схем для механических поступательных систем
- •30.2 Узловой метод построения математической модели
25.2 Использование параметрических сплайнов для интерполирования кривых
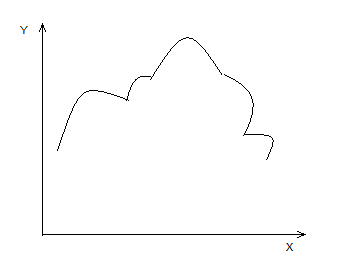
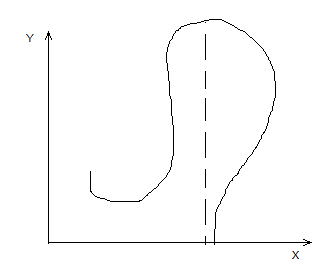
Отличие заключается в том,что для кривой возможна ситуация,когда одному знаению независ. Переменной соответствует несколько ординат точек.В том аппарате построения сплайнов который мы обсуждаем до настоящего времени было введено предположение
Когда по произвольной сис-ме точек р1,р2,р3…рn необходимо построить кривую проходящую через эту сис-му,то использовать этот аппарат невозможно,в этом случ. Можно использовать так называемые параметрические сплайны на основе обычных сплайнов можно ввести так назыв. Естественную параметризацию выбрав в качестве незав.переменгой параметр S ,который будет представлять длину дуги кривой от начальной точки до текущей тогда x=x(S); y=y(S)
В качестве простейшего примера рассмотрим интерполяцию параметрического сплайна 1 степени.
S1(x,S)=(1-t)*xi+t*xi+1
S1(y,S)=(1-t)*yi+t*yi+1
Эта пара сплайнов наз-ется параметрическими сплайнами
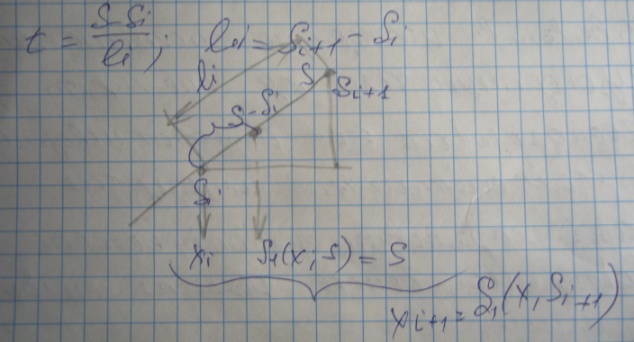
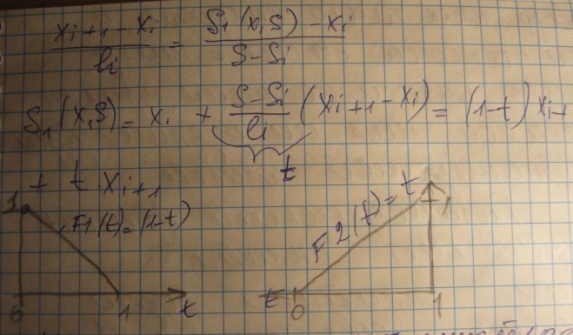
можно заметить ,что линейные функ-ии F1(t) и F2(t) являются аналогами тех ф-ий формы F1(t), F2(t), F3(t), F4(t) ,которые использовались в эрмитовом кубическом сплайне,там они были кубическими полиномами точно такие же ормулы получаются и по переменной.Отметим некоторые св-ва этого параметрического сплайна .Координаты точек такого сплайна и угол наклона касат. к нему можно вычисл. Не имея практически никакоц информации о длине дуги интерполируемой кривой.
26.1 Пример реализации метода типа Монте-Карло в среде Mathcad для вычисления площади произвольной фигуры
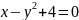
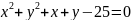

Фрагмент документа маткад:
ORIGIN:=1,
AB(x,y):=x,
Cd(x,y):=y
x:=0,y:=0 – начальные значения переменных
f(x,y):=x-y +4
g(x,y):=x + y +x+y-25
 Given
Given
f(x,y)>=0,
g(x,y)<=0,
z:=Minimize(AB,x,y) min по корд. х
a:=AВ(z1,z2)
a=-4
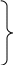 Given
Given
f(x,y)>=0,
g(x,y)<=0,
z:=Maximize(AB,x,y) max по корд. х
b:=AВ(z1,z2)
b=4.55
Given
f(x,y)>=0,
g(x,y)<=0,
z:=Minimize(Cd,x,y) min по корд. y
c:=Cd(z1,z2)
c=-2.825
Given
f(x,y)>=0,
g(x,y)<=0,
z:=Maximize(Cd,x,y) max по корд. y
d:=Cd(z1,z2)
d=2.719
Задаем число экспериментов:
N:=4000
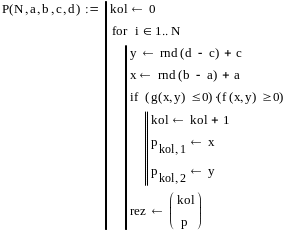
-описание процедуры,которая возвращает к-во точек из N сгенерированных и их координаты -описание процедуры,которая возвращает к-во точек из N сгенерированных и их координаты попавшие в нашу нужную область.
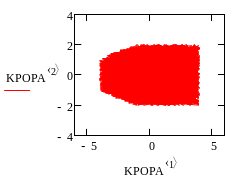
Изобразим обращение к этой процедуре:
![]()
![]()
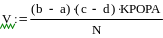
Площадь фигуры
26.2 Параметрический Эрмитов кубический сплайн.
Этот сплайн представляет собой совокупность двух Эрмитовых сплайнов.
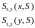
 (7)
(7)
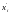 -
производная по S
от x(S)
в точке Si.
-
производная по S
от x(S)
в точке Si.
Для
возможности вычисления по формуле (7)
необходимо определить
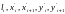 .
.
Поскольку в реальных задачах информация о наклонах обычно отсутствует, то, как и в случае обычного Эрмитова сплайна , заменим их приближенными значениями.
Поскольку точное значение параметра вычислить невозможно, то будем строить Эрмитов сплайн близкий к сплайну 7 в некотором смысле.
Во-первых, для описания сплайна введем параметризацию по суммарной длине хорд.
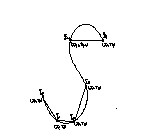
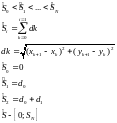

где
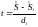
Во-вторых, точные значения производных заменим по приближенным разностным формам.
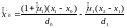 (8)
(8)
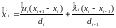 (9)
(9)
 (10)
(10)
где
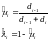
Эти формулы используются в том случае, если кривая не замкнута. Если кривая замкнута, то вместо формул 8 и 10 используем:
 (11)
(11)
Рекомендации по выбору узлов:
1.
Следует выбирать узлы так, чтобы
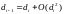 (то есть, чтобы длины звеньев были
практически одинаковы);
(то есть, чтобы длины звеньев были
практически одинаковы);
2. В точках излома кривой следует вводить по два близких узла. В этом случае будет снижена асцилляция кривой, заключающаяся в том, что сплайн сильно уклониться от истинной кривой.
