
- •Поле комплексных чисел
- •Сопряжение комплексных чисел
- •Тригонометрическая форма записи комплексных чисел
- •Комплексная экспонента
- •Извлечение корней из комплексных чисел.
- •Последовательности и ряды комплексных чисел
- •Расширенная комплексная плоскость
- •Дробно-линейная функция
- •Группа дробно-линейных преобразований сферы Римана
- •Инверсия.
- •Аналитичность
- •Гармонические функции
- •Степенные ряды
- •Основные функции комплексной переменной
- •Экспонента
- •Тригонометрические и гиперболические функции
- •Аргумент комплексного числа
- •Многозначные функции
- •Интегрирование функции комплексного переменного
- •Кривые на комплексной плоскости
- •Определение и свойства интеграла
- •Длина кривой
- •Теорема Коши
- •Теорема Коши для односвязной области
- •Распространение на многосвязные области
- •Интегральная формула Коши
- •Ряд Тейлора
- •Теорема единственности и аналитическое продолжение
- •Ряд Лорана
- •Изолированные особые точки
- •1. Особые точки
- •2. Разложение в окрестности особой точки
- •Основная теорема о вычетах
- •Вычисление интегралов с помощью вычетов
- •Литература
Основная теорема о вычетах
Пусть в проколотой окрестности точки функция аналитична. Тогда величину

где ρ -- достаточно малое положительное число, будем называть вычетом функции f(z) в точке a . Вычетом функции относительно бесконечно удаленной точки считаем величину

где C -- окружность с центром в начале координат такая, что вне круга, определяемого этой окружностью, функция f(z) особенностей не имеет.
Первичные следствия этого определения следующие:
а) вычет не зависит от величины ρ ;
б) вычет
совпадает с коэффициентом
 ряда Лорана функции f(z) в кольце 0<|z-a|
<ρ (см. формулу ( 4loran ));
ряда Лорана функции f(z) в кольце 0<|z-a|
<ρ (см. формулу ( 4loran ));
в) если f(z) аналитична в точке a или a -- устранимая особенность, то вычет в ней равен 0.
Предложение. Пусть -- полюс порядка m функции f(z). Тогда

Доказательство.
Если
-- полюс порядка m, то
 ,
где g(z) --
правильная часть, тем самым аналитическая
функция в точке
.
Тогда
,
где g(z) --
правильная часть, тем самым аналитическая
функция в точке
.
Тогда

Дифференцируя это соотношение m-1 раз, получим:

где h(a)=0. Переходя к пределу и разделив на (m-1)!, получим требуемую формулу.□
Отметим частный случай, когда -- простой полюс. Тогда

В частности,
если
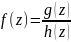 , где g(z),h(z)
аналитичны в окрестности точки
и
, где g(z),h(z)
аналитичны в окрестности точки
и
 ,
,
 ,
то
-- простой полюс и
,
то
-- простой полюс и
 .
.
Доказательство. Требует доказательства только утверждение " в частности". Из условия следует, что h(z)=(z-a)⋅s(z) для некоторой аналитичной функции s(z) такой, что s(a)≠ 0. Тогда f(z)=1/ z-a ⋅ g(z)/ s(z) и g(a) / s(a) ≠ 0. Следовательно, a -- простой полюс. Далее, переходя в следующем соотношении (z-a)f(z)= g(z) /[ (h(z)-h(a))/(z-a)] к пределу z→ a, получаем формулу Res[f(z),a]= g(a)/h'(a) .□
Основная
теорема о вычетах. Пусть f(z) аналитична
в замкнутой области D, кроме точек
 ,
лежащих внутри области D.
Тогда
,
лежащих внутри области D.
Тогда

Доказательство.
Пусть
 -- окружности достаточно малых радиусов
с центрами в точках
-- окружности достаточно малых радиусов
с центрами в точках
 такие, что круги
такие, что круги
 ими ограничиваемые, целиком лежат внутри
области D и попарно не пересекаются.
Тогда
аналитична в области
ими ограничиваемые, целиком лежат внутри
области D и попарно не пересекаются.
Тогда
аналитична в области
 и по теореме Коши имеет место равенство:
и по теореме Коши имеет место равенство:

Отсюда следует, что
∮ _ ∂ D f(z) dz=∮ _ c_1+… +c_m f(z) dz=∮ _ c_1 f(z) dz+… +∮ _ c_m f(z) dz= =2πi [Res[f(z),a_1]+… +2πi Res[f(z),a_m],
что и требовалось доказать.
Пример Вычислим интеграл:

Вычисление интегралов с помощью вычетов
Предложение.
Предположим, что бесконечно удаленная
точка является нулем второго или более
высокого порядка функции
,
т.е.
 ограничена вне круга достаточно большого
радиуса. Допустим также, что f(z) является
аналитической функцией на действительной
оси, а в верхней полуплоскости Im z>0
имеет лишь конечное число особых точек
ограничена вне круга достаточно большого
радиуса. Допустим также, что f(z) является
аналитической функцией на действительной
оси, а в верхней полуплоскости Im z>0
имеет лишь конечное число особых точек
 .
Тогда
.
Тогда

Доказательство. Все лежащие в верхней полуплоскости особые точки можно заключить внутрь расположенного в верхней полуплоскости полукруга достаточно большого радиуса R с центром в начале координат. По основной теореме о вычетах получаем
_L f(z) dz+ _ -R ^ +R f(x) dx=2πi∑_ j=1 ^n Res[f(z),a_j], (2)
где L -- верхняя полуокружность радиуса R, проходимая против часовой стрелки. Так как f(z)=g(z)/z^2 , где g(z) -- ограничена на бесконечности, например, числом M, то

при R→ +∞ . Тогда, переходя в соотношении (2) к пределу R→ +∞ , получаем требуемое равенство.
Пример. Вычислим интеграл:

Лемма К.
Жордана. Пусть на некоторой
последовательности дуг окружностей
 (
( – фиксировано) функция
– фиксировано) функция
 стремится к нулю равномерно относительно
Тогда для любого положительного числа
λ
стремится к нулю равномерно относительно
Тогда для любого положительного числа
λ

Доказательство.
Обозначим
 .
По условию леммы
.
По условию леммы
 при
при
 .
Величина
.
Величина
 также стремится к 0, причем
также стремится к 0, причем
 .
Пусть сначала a>0.
.
Пусть сначала a>0.
 E
На рис.
E
На рис.
 .
На дугах АВ и CD имеем
.
На дугах АВ и CD имеем
C
B
 ,
следовательно
,
следовательно

D
-a A
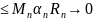 .
На основании неравенства
.
На основании неравенства
Рис.
Лемма Жордана
 ,
справедливого при
,
справедливого при
 ,
мы заключаем, что на дуге BE
имеет место неравенство
,
мы заключаем, что на дуге BE
имеет место неравенство

Следовательно,

Если для дуги
EC отсчитывать полярный
угол от отрицательной полуоси, то оценка
интеграла по этой дуге будет такая же
как и для дуги BE. Случай
 разобран. Случай
разобран. Случай
 еще проще – не надо оценивать интегралы
по дугам AB и CD.
□
еще проще – не надо оценивать интегралы
по дугам AB и CD.
□
Замечание.
Последовательность дуг
 можно заменить на семейство дуг
можно заменить на семейство дуг
 радиуса
радиуса
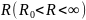 .
.
Переформулировка
леммы Жордана. Заменим
 .
Пусть на некотором семействе дуг
окружностей
радиуса
и
.
Пусть на некотором семействе дуг
окружностей
радиуса
и
 функция
функция
 стремится к нулю равномерно относительно
стремится к нулю равномерно относительно
 Тогда для любого положительного числа
t
Тогда для любого положительного числа
t

Следствие.
Пусть
 ,
причем m>0, и F(z)→
0, когда z→
∞ по любому закону, оставаясь, однако
в области Im z≥
0. Предположим, кроме того, что f(z)
аналитична, а в верхней полуплоскости
имеет не более конечного числа особых
точек
.
Тогда
,
причем m>0, и F(z)→
0, когда z→
∞ по любому закону, оставаясь, однако
в области Im z≥
0. Предположим, кроме того, что f(z)
аналитична, а в верхней полуплоскости
имеет не более конечного числа особых
точек
.
Тогда

Пример Вычислим интеграл:
_ -∞^ +∞ xcos x dx / x^2-2x+10 =_ -∞^ +∞ ze^ iz dz / z^2-2z+10 = = Re 2πi⋅ Res[ze^ iz/ z^2-2z+10 ,1+3i] =Re 2πi(1+3i)e^(-3+i)/2(1+3i)-2 = 3πe^(-3)(cos1-3sin1).
Интеграл
Дирихле. Вычислим следующий интеграл:
 .
Он равен интегралу
.
Он равен интегралу
 . Имеем:
. Имеем:

Отсюда следует равенство:
 .
.
