20. Изолированные особые точки

1. Особые точки

Особая точка функции комплексного переменного -- это точка, в которой отсутствует аналитичность. Особая точка функции f(z) называется изолированной, если в некоторой окрестности этой точки функция f(z) не имеет других особых точек.

2. Разложение в окрестности особой точки

Пусть – изолированная особая точка, и R – расстояние от до ближайшей особой точки. Так как – изолированная особая точка, то 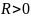. Разложим в ряд Лорана в кольце .

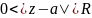Рассмотрим три случая.

Случай 1. В ряде Лорана главная часть отсутствует. Тогда, доопределяя функцию в точке a посредством равенства 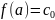, получаем аналитическую в точке функцию, которую также будем обозначать через . Точка в этом случае называется устранимой особой точкой.

Пример. Точка 0 для функции 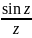устранима и функция

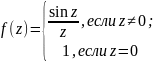
будет аналитическим продолжением функции на всю комплексную плоскость.

Теорема. В устранимой особой точке функция имеет предел. Наоборот, если аналитическая функция в изолированной особой точке ограничена, то эта особенность устранима.

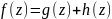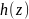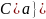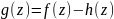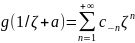Доказательство. Первая часть предложения доказана выше. Пусть f(z) имеет изолированную особенность в точке и -- разложение на главную и правильную части в этой точке. Тогда аналитична в точке , а продолжается на всю область и ограничена на бесконечности. Если ограничена в точке , то и также ограничена в точке . Тогда функция аналитична на всей комплексной плоскости и ограничена. По теореме Лиувилля эта функция должна быть константой. Так как при 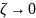эта функция обращается в ноль, то g≡ 0. Тем самым главная часть в разложении в ряд Лорана функции f(z) отсутствует, что и требовалось доказать.

Случай : главная часть ряда Лорана ненулевая и содержит конечное число слагаемых. Имеем:

f(z)=∑_ n=0 ^∞ c_n(z-a)^n + c_-1/z-a +c_-2/(z-a)^2 +c_-3/(z-a)^3 +...+c_-m/(z-a)^m ,

где 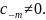В этом случае a называется полюсом порядка m . Если m=1, то a называется простым полюсом

Теорема. Точка a -- полюс порядка m тогда и только тогда, когда 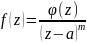, где 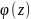-- аналитическая и не равная 0 в точке a функция.

Изолированная особая точка a функции f(z) является полюсом тогда и только тогда, когда то выполняется равенство .

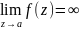Доказательство. Если lim_ z→a f(z)=∞, то lim_ z→a \frac 1/ f(z) =0. Кроме того, из равенства lim_ z→a f(z)=∞ следует, что f(z)≠ 0 в достаточно малой окрестности точки a и тем самым эта особенность изолирована для функции 1/ f(z) . Следовательно, a -- устранимая особенность для функции 1/ f(z) по теореме п.2 и 1/ f(z) =(z-a)^nψ (z) для некоторого n≥ 0 и аналитической функции ψ (z) такой, что ψ (a)≠ 0. Тогда f(z)=𝜑(z)/(z-a)^n для 𝜑(z)=1/ψ (z) -- аналитической функции в точке a. Остается применить предыдущую теорему.

Случай 3: главная часть ряда Лорана содержит бесконечное число слагаемых.

В этом случае a называется существенной особой точкой.

Теорема Ю.В. Сохоцкого. Если -- существенная особая точка функции , то для любого A∈ ℂ или A=∞ найдется последовательность точек 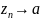и отличных от , такая, что .

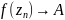Доказательство. Пусть сначала A=∞ . Согласно теореме выше функция f(z) не может быть ограниченной в точке a. Следовательно, требуемая последовательность существует. Пусть теперь A∈ ℂ . Рассмотрим функцию 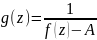. Если устранима или является полюсом для g(z), то такова же она будет и для f(z). Следовательно, -- существенная особенность функции g(z). Пусть последовательность такова, что 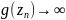. Тогда .

Пример. Точка 0 -- существенная особенность функци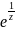и , так как разложение в ряд Лорана для этой функции в области ℂ * имеет вид 1+1/ z +1/z^22! +1/z^33! +… Для последовательности 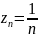имеем: 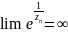а для последовательности 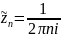, также сходящейся к 0, имеем: .
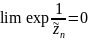