Вопрос 24

Параметрическое уравнение линии на плоскости

Параметрич. Ур-е окружности

Пусть в прямоугольной системе координат дана окружность

Рассмотрим ее произвольную точку M(x;y)

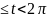Пусть радиус-вектор   точки М образует угол величины t с положительным направлением оси ОХ, тогда абсцисса и ордината точки М изменяются в зависимости от t (0 ) . Выражая х и у через t , находим

 (0 )

Параметрические уравнения эллипса.

Теорема. Пусть 0<b<a – произвольные действительные числа. Тогда система уравнения

                           ,                            

является параметрическими уравнениями эллипса в канонических для эллипса системе координат.

 Параметрические уравнения параболы: 

Параметрические уравнения циклоиды:

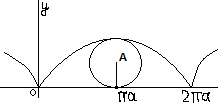
Пусть окружность без скольжения катится по прямой. Тогда точка такой окружности описывает кривую, которая называется циклоидой.

Выясним, как выглядит уравнение циклоиды. Для этого предположим, что окружность радиуса А катится по оси ОХ и что мы следим за траекторией точки, имевшей вначале координаы (0,0).

После того, как окружность повернулась на угол t? эта точка заняла положение точки М(х,у), как показано на рисунке. Так как нет скольжения, то длинна отрезка ОА должна равнятся длинне дуги АМ = at. Поэтому х = ОА – sint = at – a sint = a(t – sint). Далее, из элементарных геометрицеских соображений видно, что должно быть y = a – a cost = a(1 – cost). Итак, мы получили параметрическое уравнение циклоиды

Заметим, что при t [0,2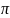 ] уравнение описывает первую арку циклоиду.

Вопрос 23

Пусть y = f(x) дифференцируемая функция, а ее аргумент x – независимая переменная. Тогда ее первый дифференциал dy = есть также функция x; можно найти дифференциал этой функции.

Дифференциал от дифференциала функции y = f(x) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается 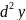или .

Итак, по определению = d(dy). Найдём выражение второго дифференциала функции y = f(x).

Так как dx = не зависит от x, то при дифференцировании считаем dx постоянным:

т.е. (1)

Здесь d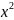 обозначает (dx

Аналогично определяется и находится дифференциал третьего порядка:

И, вообще, дифференциал n – го порядка есть дифференциал от дифференциала (n – 1) – го порядка:

Отсюда находим, что 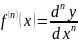. В частности, при n =1, 2, 3 соответственно получаем:

Т.е. производную функции можно рассматривать как отношение ее дифференциала соответствующиго порядка к соответствующей степени дифференциала независимой переменной.

Отметим, что все приведённые выше формулы справедливы только, если Х – независимая переменная. Если же функцию y = f(x), где Х – функция от какой – то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.

Используя формулу дифференциала произведения (d(u*v)=v du + u dv), получаем:

(2)

Т.е.

Сравнивая формулы (1) и (2), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое

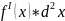
Ясно, что если ч – независимая переменная, то

и формула (2) переходит в формулу (1)