Вопрос 33
33.1)1-ое достаточное условие экстремума
Если непрерывная функция y=f(x) дифференцируема в некоторой бета-окрестности крит точки x0 и при переходе через нее(слева направо) производная меняет знак с плюса на минус, то х0 есть точка максимума; с минуса на плюс- точка минимума.
2)если в точке х0 первая производная функции f(x) равна нулю,а вторая производная в этой же точке сущ. И отлична от 0, то при второй производной меньше 0 в точке х0 ф-ция имеет максимум
И миниму при второй производной больше 0
Вопрос 32
32.Экстремум- значение функции в точке максимума(минимума).Достаточное условие экстремума-ЕСЛи дифферинцируемая ф-ция у=f(x) имеет экстремум в точке x0, то ее производная в этой точке равна нулю: f`(x0)=0
Экстремумы, их необходимые и достаточные условия
1 Функция f(x) имеет мин в точке x₀, если сущ такая окрестность этой точки (x₀-δ, x₀+δ),
Что для∀ x∈(x₀-δ,x₀+δ) выполняется условие f(x₀)<=f(x).
2 Функция f(x) имеет мин в точке x₀, если сущ такая окрестность этой точки (x₀-δ, x₀+δ),
Что для ∀x∈(x₀-δ,x₀+δ) выполняется условие f(x₀)<=f(x).
Теорема о необходимом условии экстремума:
Если дифференцируемая функция f(x) в точке x₀ имеет экстремум, то f’(x)=0.
Это равенство необходимо, но не достаточно для сущ экстремума в точке x₀,
Т.к если при переходе ф-ции через точку x₀ знак производной не поменяется =>
Значит функция продолжает убывать или возростать и в этой точке нет ни min ни max!
Теорема о достаточном условии экстремума:
Если производная f’(x) меняет знак с + на - ―при переходе через точку x₀, то в точке x₀
ф-ция f(x) имеет max.
Если производная f’(x) меняет знак с - на + ―при переходе через точку x₀, то в точке x₀
ф-ция f(x) имеет min.
Вопрос 30
Правило Лопиталя. Примеры.
Метод
нахождения пределов функций, раскрывающий
неопределённости вида 0/0 и
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу
отношения их производных.
На
промежутке [a;b] заданы две функции
и
,
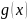имеющие производные, причём f(a)=g(a)=0.
Т.к. эти фу-ции имеют производные, то
они непрерывны, а потому
и
при
.
Значит
если предел отношения производных
существует.
используя теорему
Коши(Теорема
Коши.
,
где C
(a,b)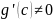
),
получим
,
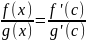где a
< c
< x
Ясно,
что
при
,
поэтому
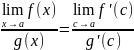
Но
Значит,
Примеры :
1.)
2.)
=
“можно применить правило Лопиталя 3
раза (а лучше разделим на x 3)”
=
Билет 31
Условия возрастания и убывания функции.
Функция называется возрастающая на промежутке Х, если любой x1, x2 принадлежит X при том, что x1<x2, следовательно f(x1)<f(x2)
Функция называется неубывающей на промежутке Х, если любой x1, x2 принадлежит X при том, что x1<x2, следовательно f(x1)≤f(x2)
Функция называется возрастающая на промежутке Х, если любой x1, x2 принадлежит X при том, что x1<x2, следовательно f(x1)>f(x2)
Функция называется возрастающая на промежутке Х, если любой x1, x2 принадлежит X при том, что x1<x2, следовательно f(x1)≥f(x2)
Достаточное условие.
Если функция f(x) дифференцируема в точке x0, f’(x0)=0 и f’(x) меняет знак через точку x0, то f(x) в точке x0 имеет экстремум.
Если f’(x) при переходе через точку x0 меняет знак с + на -, то x0 точка максимума, а если с – на +, то x0 точка минимума.
2)Если функция f(x) дважды дифференцируема в точке x0, f’(x0)=0 и f’’(x0)≠0, то в точке x0 функция имеет максимум при f’’(x0)<0, если f’’(x0)>0, то f(x) минимум.