2.2. Описание случайных погрешностей с помощью функций распределения

Р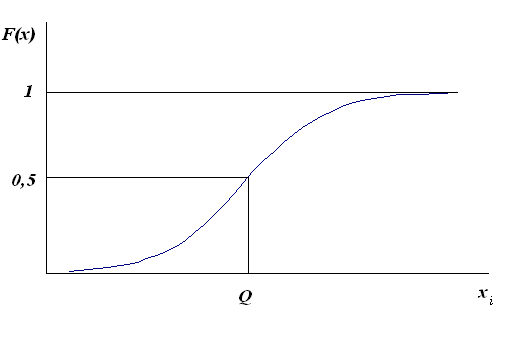 ассмотрим результат наблюдений за постоянной физической величиной как случайную величину, принимающую различные значения x_i. Тогда интегральной функцией распределения результатов наблюдения называют зависимость вероятности того, что результат наблюдения в i-ом опыте окажется меньше некоторого текущего значения x_i:

.

Часто при интегральная функция распределения имеет значение 0,5, и в этой точке находится точка перегиба. В этом случае говорят о симметричности распределения результатов относительно истинного значения измеряемой величины.

Б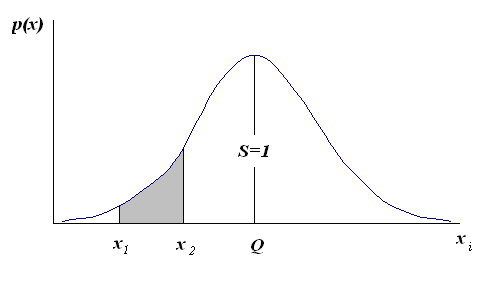 олее наглядной является дифференциальная функция распределения результатов наблюдения, иначе называемая плотностью распределения вероятности. Дифференциальная функция распределения является функцией, производной от интегральной функции по своему аргументу.

; .

Где - это распределение вероятности или плотность распределения результатов, или дифференциальная функция распределения. - Вероятность того, что при измерениях появится число меньшее либо равное некоторому фиксированному значению. Полученное значение даст функцию распределения вероятности отсчета.

П лощадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна 1. А это означает, что вероятность результатов измерения, лежащих в пределах равна 100%.

Определим вероятность того, что результат наблюдения при проведении измерений примет некоторое конкретное значение, которое находится в интервале .

.

Произведение, стоящее под интегралом - элемент вероятности, и оно равно вероятности того, что случайные величины примут некоторое значение в интервале . Поэтому по форме кривой дифференциальной функции распределения можно судить, какие интервалы значений случайных измерений более вероятны, какие менее. Для дифференциальной функции распределения наиболее вероятное значение – это значение, лежащее вблизи вершины распределения, а следовательно вблизи истинного значения измеряемой величины.

2.3. Числовые характеристики или моменты случайных величин.

Описание результатов измерения с помощью законов распределения является наиболее полным, но не всегда удобным. Во многих случаях ограничиваются приближенным описанием закона распределения с помощью его числовых характеристик (моментов). Все они представляют собой некоторые усредненные значения. Причем, если усредняемые величины отсчитываются от начала координат, то момент называется начальными; если от центра закона распределения, то центральными.

Начальные моменты

, где - номер момента.

Важнейшим начальным моментом является 1-ый, который называется средним значением или математическим ожиданием и определяется по формуле

.

Центральные моменты

.

1-ый центральный момент

, т.к. .

2-ой центральный момент - дисперсия

.

Чем больше дисперсия, тем значительнее рассеяние результатов измерения.

В метрологии часто используется понятие среднего квадратичного отклонения

.

3-ий центральный момент применяется как мера несимметричности распределения. С его помощью определяют величину асимметрии

.

Если , распределение симметрично.

4-ый центральный момент используется для оценки заостренности дифференциальной функции распределения. При помощи его определяется эксцесс

.

Чем больше , тем более заострена вершина кривой распределения. Для распределения Гаусса (нормальное распределение) - .