
НОУ ВПО ИНСТИТУТ ЗАКОНОВЕДЕНИЯ И УПРАВЛЕНИЯ
ВСЕРОССИЙСКОЙ ПОЛИЦЕЙСКОЙ АССОЦИАЦИИ
Контрольные задания и методические рекомендации
для выполнения контрольной работы
по дисциплине «Математика»
для студентов заочной формы обучения
специальности 061100 «Менеджмент организации»
(1 курс, 1 семестр)
Тула 2011
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Настоящее пособие предназначено для студентов заочного отделения института законоведения и управления всероссийской полицейской ассоциации, для которых учебным планом предусмотрено изучение курса математики в объеме 550 учебных часов. Контрольная работа охватывают следующие темы курса математики: «Векторная и линейная алгебра с элементами аналитической геометрии»; «Дифференциальное исчисление функции одного переменного».
Пособие содержит задания по выполнению контрольной работы, краткий теоретический и справочный материал, а также решения некоторых задач, тщательный разбор которых поможет студенту-заочнику выполнить данную контрольную работу. Контрольная работа составлена по десятивариантной системе. Это позволило отразить в них более широкий круг вопросов программы. В качестве методического руководства также следует рассматривать рабочую тетрадь, работа с которой позволит студентам-заочникам повысить степень своей подготовленности по каждой теме курса математики.
Контрольная работа должна быть выполнена в отдельной тетради, на обложке тетради должны быть указаны фамилия студента, его инициалы, полный учебный шифр, номер варианта контрольной работы, название дисциплины. В работу должны быть включены все задачи, указанные в задании по варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.
Задачи контрольной работы следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Перед решением каждой задачи надо полностью переписать ее условие.
Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
Чертежи и графики должны быть выполнены с указанием единиц масштаба, координатных осей и других элементов чертежа. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже.
Для замечаний преподавателя необходимо на каждой странице оставлять поля шириной 2–3 см.
После получения рецензии на сданную на проверку работы студент должен исправить все отмеченные ошибки и недочеты. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента.
Вносить исправления в текст работы после ее рецензирования запрещается.
Студент выполняет вариант контрольной работы, совпадающий с последней цифрой его учебного шифра. Требуется представить решение семи указанных ниже задач. Таким образом, например, студент, имеющий шифр ***6, должен решить задачи №№6, 26, 36, 46, 56(а,б,в,г).
График выполнения контрольной работы
Выдача |
Установочная сессия |
Сдача |
Не позднее 10 дней до сессии1 |
Контроль |
Зачет |
Задача 1.
Даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр.
А(–5; 0), В(7; 9), С(5; –5).
А(–7; 2), В(5; 11), С(3; –3).
А(–5; –3), В(7; 6), С(5; –8).
А(–6; –2), В(6; 7), С(4; –7).
А(–8; –4), В(4; 5), С(2; –9).
А(0; –1), В(12; 8), С(10; –6).
А(–6; 1), В(6; 10), С(4; –4).
А(–2; –4), В(10; 5), С(8; –9).
А(–3; 0), В(9; 9), С(7; –5).
А(–9; –2), В(3; 7), С(1; –7).
Задача 2.
Составить
уравнение линии, для каждой точки которой
отношение расстояний до точки А(х1;
у1)
и до прямой
![]() равно числу ε.
Полученное уравнение привести к
простейшему виду и построить кривую.
равно числу ε.
Полученное уравнение привести к
простейшему виду и построить кривую.
А(4; 0), а = 9,
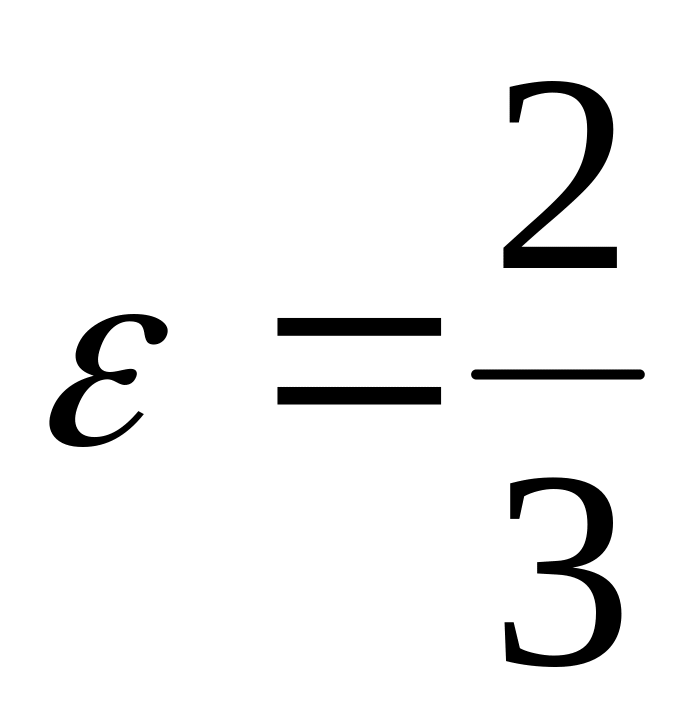 .
.А(–8; 0), а = –2,
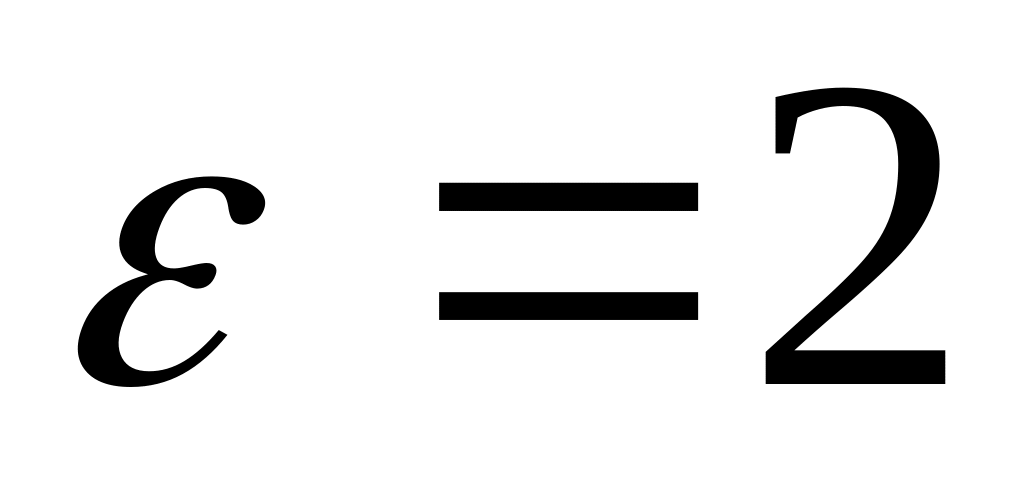 .
.А(4; 0), а = 1, .
А(9; 0), а = 4,
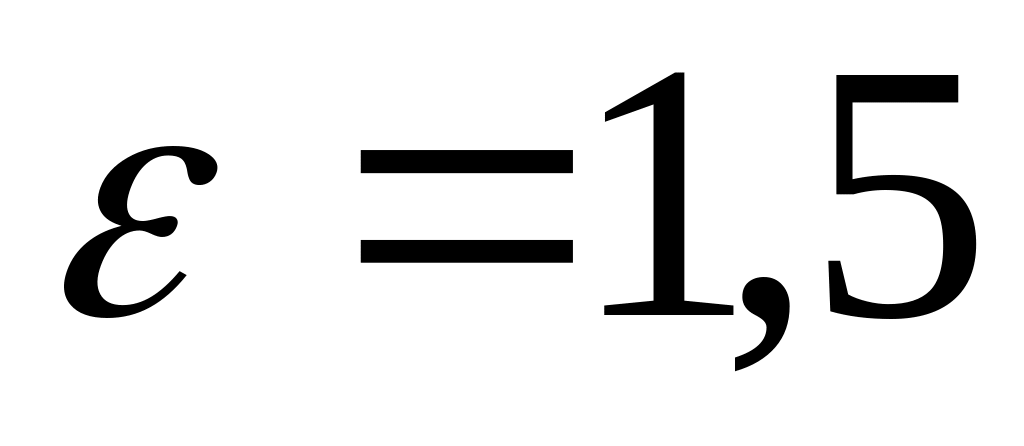 .
.А(–1; 0), а = –4,
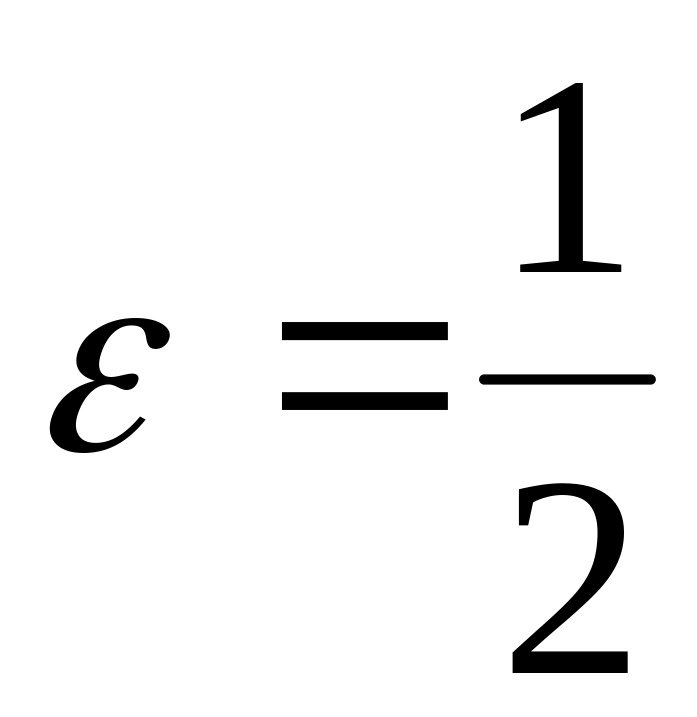 .
.
Составить
уравнение линии, для каждой точки которой
ее расстояние до точки А(х1;
у1)
равно расстоянию до прямой
![]() .
Полученное уравнение привести к
простейшему виду и построить кривую.
.
Полученное уравнение привести к
простейшему виду и построить кривую.
А(2; 1), b = –1.
А(–2; –2), b = –4.
А(2; –1), b = 2.
А(2; –1), b = 1.
А(4; –1), b = 1.
Задача 3.
В
задачах 1–10 даны координаты точек А,
В,
С.
Требуется: 1) записать векторы
![]() и
и
![]() и найти модули этих векторов; 2) найти
угол между векторами
и
;
3) составить уравнение плоскости,
проходящей через точку С
перпендикулярно вектору
и изобразить ее на чертеже, используя
уравнение плоскости «в отрезках».
и найти модули этих векторов; 2) найти
угол между векторами
и
;
3) составить уравнение плоскости,
проходящей через точку С
перпендикулярно вектору
и изобразить ее на чертеже, используя
уравнение плоскости «в отрезках».
31. А(7; –4; 1), В(12; –3; 1), С(10; 1; 5).
32. А(0; –3; 3), В(5; –2; 3), С(3; 2; 7).
33. А(–2; –1; –2), В(3; 0; –2), С(1; 4; 2).
34. А(–6; 0; 0), В(–1; 1; 0), С(–3; 5; 4).
35. А(–2; –3; –8), В(3; –2; –8), С(1; 2; –4).
36. А(1; 0; –1), В(6; 1; –1), С(4; 5; 3).
37. А(–1; 4; 1), В(4; 5; 1), С(2; 9; 5).
38. А(3; –6; –3), В(8; –5; –3), С(6; –1; 1).
39. А(1; 0; 0), В(6; 1; 0), С(4; 5; 4).
40. А(2; –8; –2), В(7; –7; –2), С(5; –3; 2).
Задача 4.
Систему уравнений записать в матричной форме и решить методом Гаусса, с помощью правила Крамера и с помощью обратной матрицы.
41.
![]() 42.
42.
![]()
43.
![]() 44.
44.
![]()
45.
![]() 46.
46.
![]()
47.
![]() 48.
48.
![]()
49.
![]() 50.
50.
![]()
Задача 5.
В задачах 51–60 найти указанные пределы.
51.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
52.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
53.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
54.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
55.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
56.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
57.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
58.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
59.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
60.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Даны вершины треугольника АВС: А(–4; 8), В(5; –4), С(10; 6).
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр.
Решение.
1. Расстояние
![]() между точками
между точками
![]() и
и
![]() определяется по формуле:
определяется по формуле:
![]() . (1)
. (1)
Подставив в эту формулу координаты точек А и В, имеем:
![]() .
.
2. Уравнение прямой, проходящей через точки и , имеет вид:
![]() . (2)
. (2)
Подставив в (2) координаты точек:
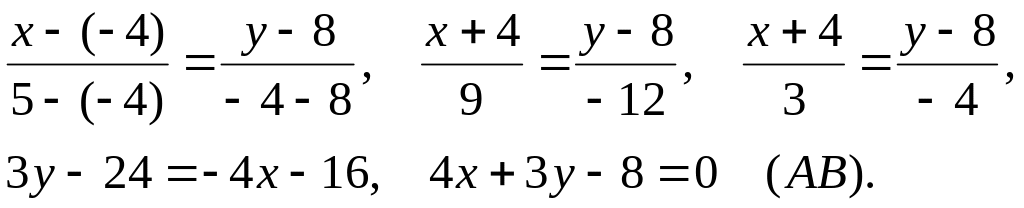
Для
нахождение углового коэффициента
![]() прямой АВ
разрешим полученное уравнение относительно
у:
прямой АВ
разрешим полученное уравнение относительно
у:
![]() .
Отсюда
.
Отсюда
![]() .
Подставив в формулу (2) координаты точек
А
и С,
получим уравнение прямой АС.
.
Подставив в формулу (2) координаты точек
А
и С,
получим уравнение прямой АС.
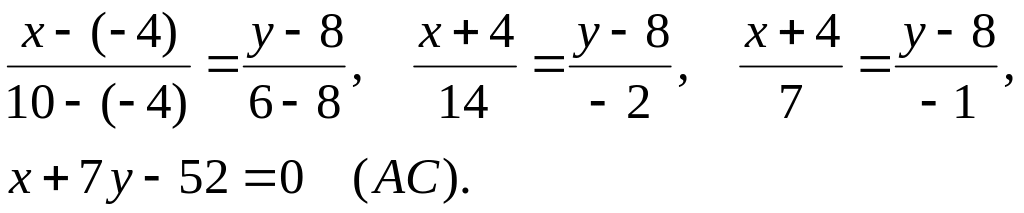
Отсюда
![]() .
.
3.
Угол
![]() между двумя прямыми, угловые коэффициенты
которых равны
между двумя прямыми, угловые коэффициенты
которых равны
![]() и
и
![]() ,
определяется по формуле:
,
определяется по формуле:
![]() . (3)
. (3)
Угол
А,
образованный прямыми АВ
и АС,
найдем по формуле (3), подставив в нее
![]() ,
,
![]() .
.
 ,
,
![]() рад.
рад.
4.
Так как высота![]() перпендикулярна стороне
перпендикулярна стороне
![]() ,
то угловые коэффициенты этих прямых
обратны по величине и противоположны
по знаку, т.е.
,
то угловые коэффициенты этих прямых
обратны по величине и противоположны
по знаку, т.е.
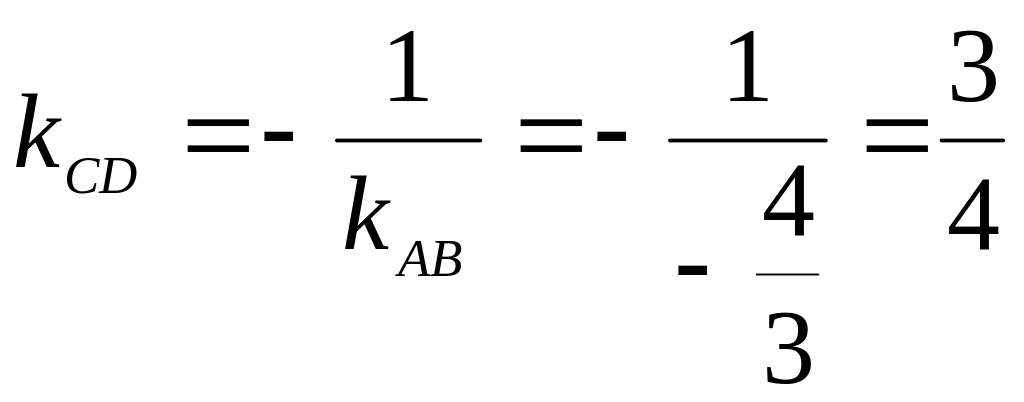 .
.
Уравнение
прямой, проходящей через данную точку
в заданном угловым коэффициентом
![]() направлении, имеет вид:
направлении, имеет вид:
![]() . (4)
. (4)
Подставив
в (4) координаты точки С
и
![]() ,
получим уравнение высоты
:
,
получим уравнение высоты
:
![]() . (5)
. (5)
Для
нахождения длины
определим координаты точки
![]() ,
решив систему уравнений (АВ)
и (
):
,
решив систему уравнений (АВ)
и (
):
![]()
откуда
![]() ,
то есть
,
то есть
![]() .
.
Подставив в формулу (1) координаты точек С и , находим:
![]() .
.
5.
Уравнение окружности радиуса
![]() с центром в точке
с центром в точке
![]() имеет вид:
имеет вид:
![]() . (6)
. (6)
Так как является диметром искомой окружности, то ее центр Е есть середина отрезка . Воспользовавшись формулами деления отрезка пополам, получим:
![]()
Следовательно,
![]() и
и
![]() .
Используя формулу (6), получаем уравнение
искомой окружности:
.
Используя формулу (6), получаем уравнение
искомой окружности:
![]() .
.
На
рис. 1 в декартовой прямоугольной системе
координат
![]() изображен треугольник
изображен треугольник
![]() ,
высота
,
окружность с центром в точке Е.
,
высота
,
окружность с центром в точке Е.
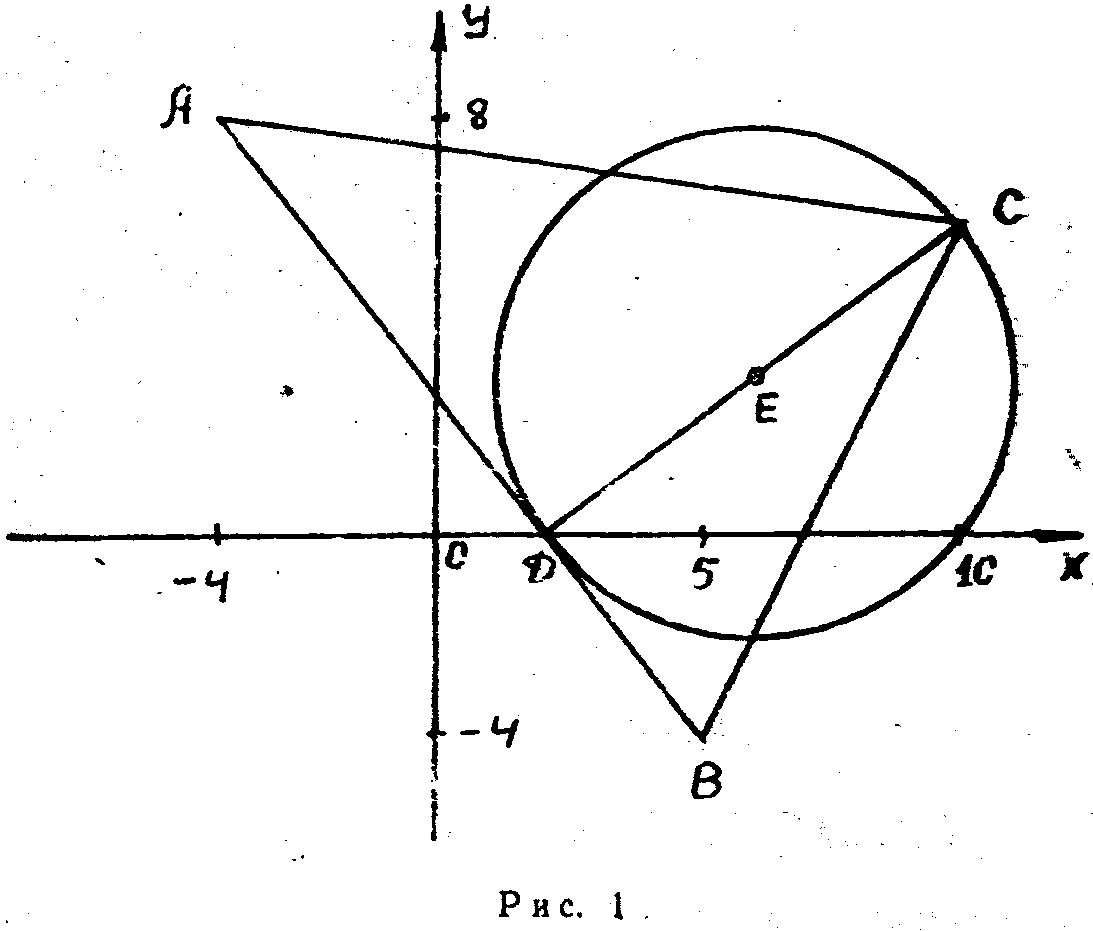
Задача
2. Составить
уравнение линии, для каждой точки которой
отношение расстояний до точки
![]() и до прямой
и до прямой
![]() равно числу
равно числу
![]() .
Полученное уравнение привести к
простейшему виду и построить кривую.
.
Полученное уравнение привести к
простейшему виду и построить кривую.
Решение.
Пусть
![]() – текущая (произвольная) точка искомого
геометрического множества точек. Опустим
перпендикуляр
– текущая (произвольная) точка искомого
геометрического множества точек. Опустим
перпендикуляр
![]() на прямую
(рис. 2). Тогда
на прямую
(рис. 2). Тогда
![]() .
По условию задачи
.
По условию задачи
![]() .
По формуле (1) из предыдущей задачи
.
По формуле (1) из предыдущей задачи
![]() .
.
Тогда
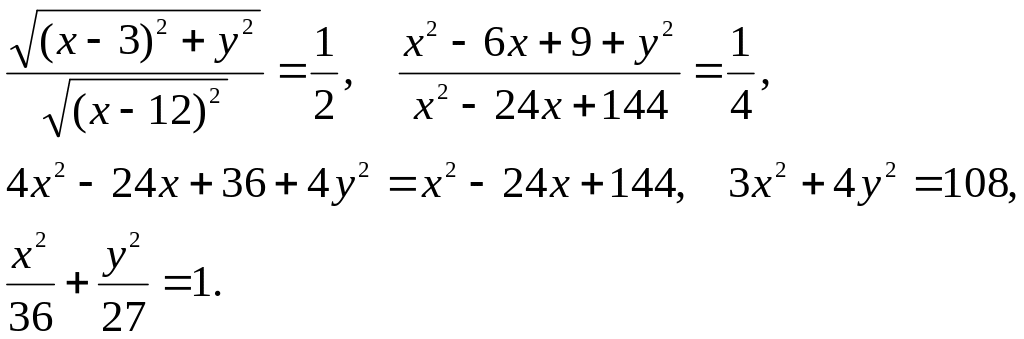
Полученное
уравнение представляет собой эллипс
вида
![]() ,
где
,
где
![]() .
.
Определим
фокусы эллипса
![]() и
и
![]() .
Для эллипса справедливо равенство
.
Для эллипса справедливо равенство
![]() ,
откуда
,
откуда
![]() и
и
![]() .
То есть
.
То есть
![]() и
и
![]() – фокусы эллипса (точки
– фокусы эллипса (точки
![]() и А
совпадают).
и А
совпадают).
Эксцентриситет
эллипса
![]() .
.
 у
у
![]() М
В
М
В

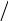

F1 А

–3 0 3 6 12 х
Рис. 2
Задача
3. Составить
уравнение геометрического места точек,
отношение расстояний которых до точки
![]() и до прямой
и до прямой
![]() равно числу
равно числу
![]() .
.
 Решение.
Пусть
– произвольная точка искомого
геометрического множества точек. Опустим
перпендикуляр
на прямую
и определим координаты точки В
(рис. 3). Очевидно, что абсцисса точки
Решение.
Пусть
– произвольная точка искомого
геометрического множества точек. Опустим
перпендикуляр
на прямую
и определим координаты точки В
(рис. 3). Очевидно, что абсцисса точки
![]() равна
равна
![]() (так как точка В
лежит на прямой
),
а ордината точки В
равна ординате точки М.
Следовательно, имеем:
(так как точка В
лежит на прямой
),
а ордината точки В
равна ординате точки М.
Следовательно, имеем:
![]() .
.
у
4 В М
–2 0 2 4 А 6 х
–2
Рис. 3
По
условию задачи
![]() ;
так как
;
так как
![]() ,
то получаем:
,
то получаем:
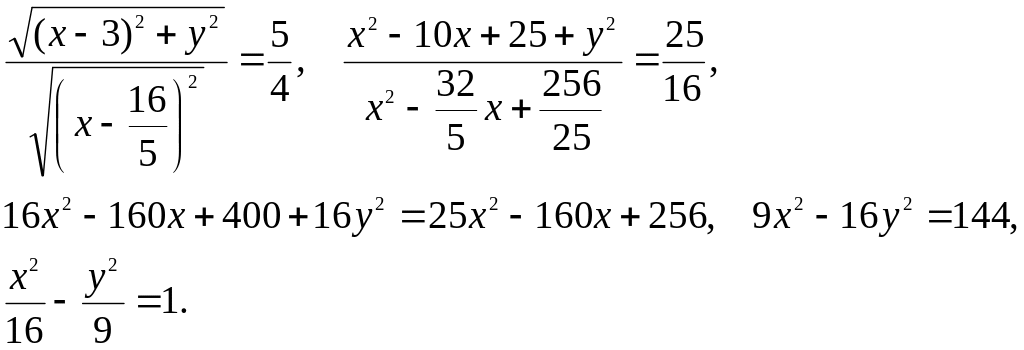
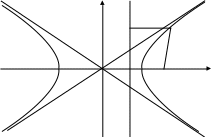
Полученное
уравнение представляет собой гиперболу
вида
![]() ,
где
,
где
![]() .
.
Задача
4. Составить
уравнение линии, для каждой точки которой
ее расстояние до точки
![]() равно расстоянию до прямой
равно расстоянию до прямой
![]() .
Полученное уравнение привести к
простейшему виду и построить кривую.
.
Полученное уравнение привести к
простейшему виду и построить кривую.
Решение.
– текущая точка искомой кривой. Опустим
из точки М
перпендикуляр МВ
на прямую
(рис. 4). Тогда
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() или
или

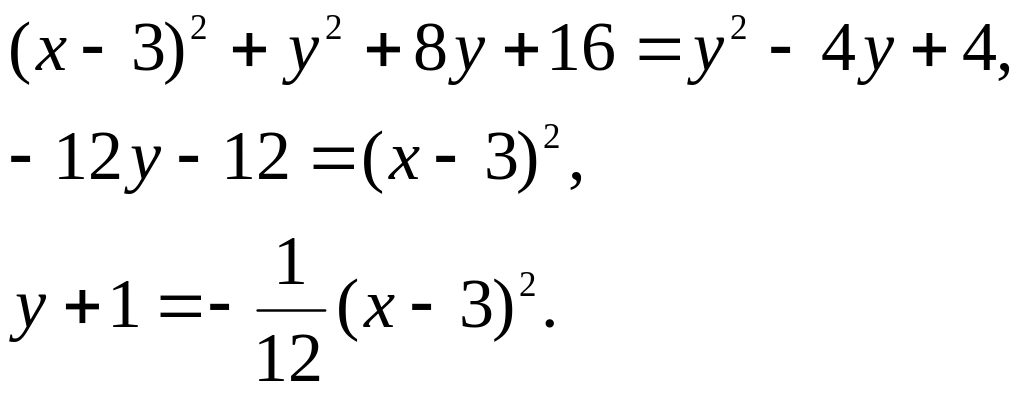
у У’
2 В
0 3 х
Х’
–4 А
Рис. 4
Полученное
уравнение определяет параболу с вершиной
в точке
![]() .
Для приведения уравнения параболы к
простейшему (каноническому) виду положим
.
Для приведения уравнения параболы к
простейшему (каноническому) виду положим
![]() ,
,
![]() .
Тогда в системе координат
.
Тогда в системе координат
![]() уравнение параболы принимает следующий
вид:
уравнение параболы принимает следующий
вид:
![]() .
В системе координат
строим параболу.
.
В системе координат
строим параболу.
Задача 5. Даны координаты трех точек: А(3; 0; –5), В(6; 2; 1), С(12; –12; 3).
Требуется: 1) записать векторы и в системе орт и найти модули этих векторов; 2) найти угол между векторами и ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору .
Решение.
1) Если даны точки
![]() и
и
![]() ,
то вектор
,
то вектор
![]() через орты
через орты
![]() выражается следующим образом:
выражается следующим образом:
![]() .
.
Подставляя в эту формулу координаты точек А и В, имеем:
![]() .
.
Аналогично
![]() .
.
Модуль вектора вычисляется по формуле
![]() .
.
Подставляя
в формулу найденные ранее координаты
векторов
![]() и
и
![]() ,
находим их модули:
,
находим их модули:
![]() ,
,
![]() .
.
2)
Косинус угла
,
образованного векторами
![]() и
и
![]() ,
равен их скалярному произведению,
деленному на произведение их модулей
,
равен их скалярному произведению,
деленному на произведение их модулей
![]() .
.
Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных произведений одноименных координат, то
![]() .
.
Тогда
![]() .
.
3)
Уравнение плоскости, проходящей через
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() ,
имеет вид
,
имеет вид
![]() .
.
По
условию задачи искомая плоскость
проходит через точку
![]() перпендикулярно
вектору
перпендикулярно
вектору
![]() .
Подставляя
.
Подставляя
![]()
![]()
![]()
![]() ,
получим:
,
получим:
![]()
![]() – искомое уравнение плоскости.
– искомое уравнение плоскости.
Перенеся свободный член -30 в правую часть тождества и разделив на 30 все члены выражения, получим уравнение плоскости «в отрезках»:
![]() .
.
Строим чертеж

Задача 6. Данную систему уравнений записать в матричной форму и решить ее с помощью обратной матрицы:
![]()
Решение.
Обозначим через А
– матрицу коэффициентов при неизвестных;
Х
– матрицу-столбец неизвестных
![]() ;
Н
– матрицу-столбец свободных членов:
;
Н
– матрицу-столбец свободных членов:
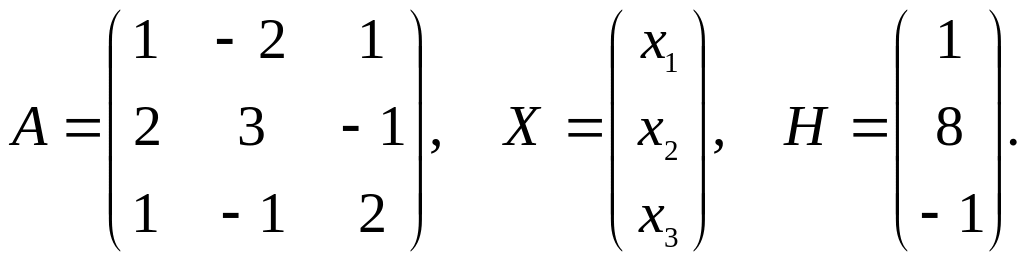
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
![]() . (1)
. (1)
Если
матрица А
– невырожденная (ее определитель
![]() отличен от нуля), то она имеет обратную
матрицу
отличен от нуля), то она имеет обратную
матрицу
![]() .
Умножив обе части уравнения (1) на
,
получим:
.
Умножив обе части уравнения (1) на
,
получим:
![]() . (2)
. (2)
Но
![]() (Е
– единичная матрица), а
(Е
– единичная матрица), а
![]() ,
поэтому
,
поэтому
![]() .
.
Равенство
(2) называется матричной записью решения
системы линейных уравнений. Для нахождения
решения системы уравнений необходимо
вычислить обратную матрицу
![]() .
.
Пусть имеем невырожденную матрицу
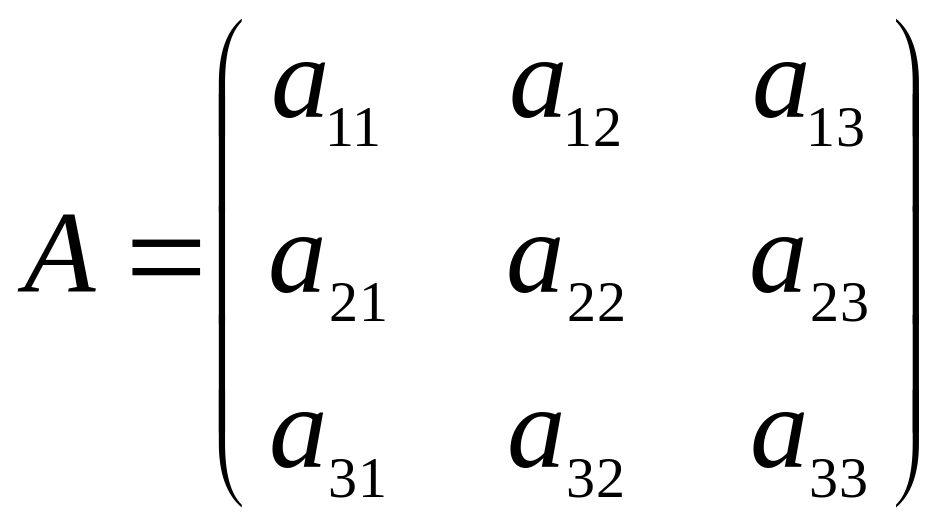 .
Тогда
.
Тогда
 ,
,
где
![]() – алгебраическое дополнение элемента
– алгебраическое дополнение элемента
![]() в определителе матрицы А,
которое является произведением
в определителе матрицы А,
которое является произведением
![]() на минор (определитель) второго порядка,
полученный вычеркиванием
на минор (определитель) второго порядка,
полученный вычеркиванием
![]() -ой
строки и
-ой
строки и
![]() -го
столбца в определителе матрицы А.
-го
столбца в определителе матрицы А.
Вычислим
определитель
и алгебраические дополнения
![]() элементов матрицы А.
элементов матрицы А.
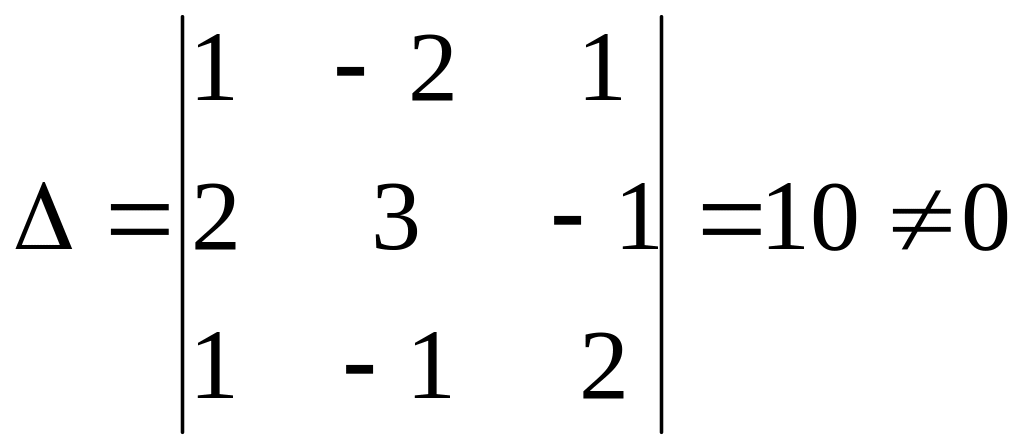 – следовательно матрица А
имеет обратную матрицу
.
– следовательно матрица А
имеет обратную матрицу
.
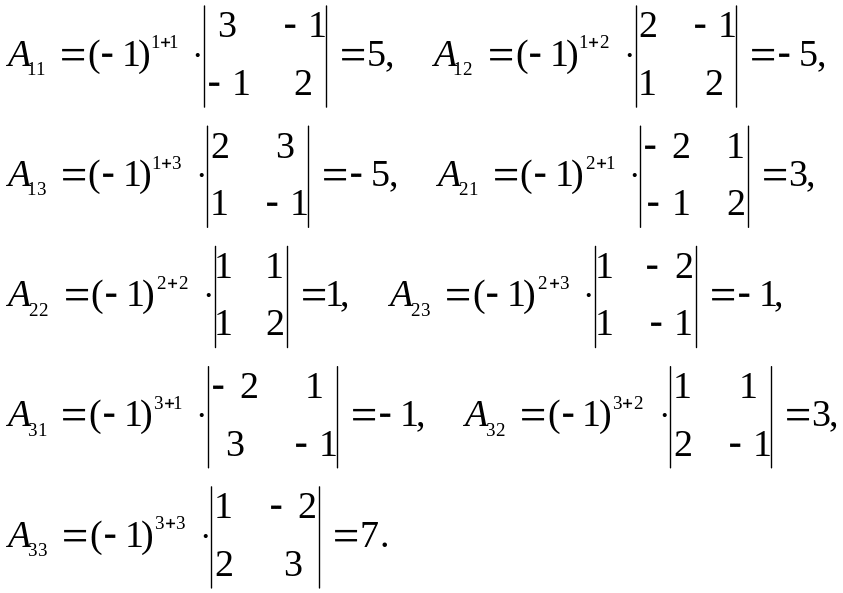
Тогда
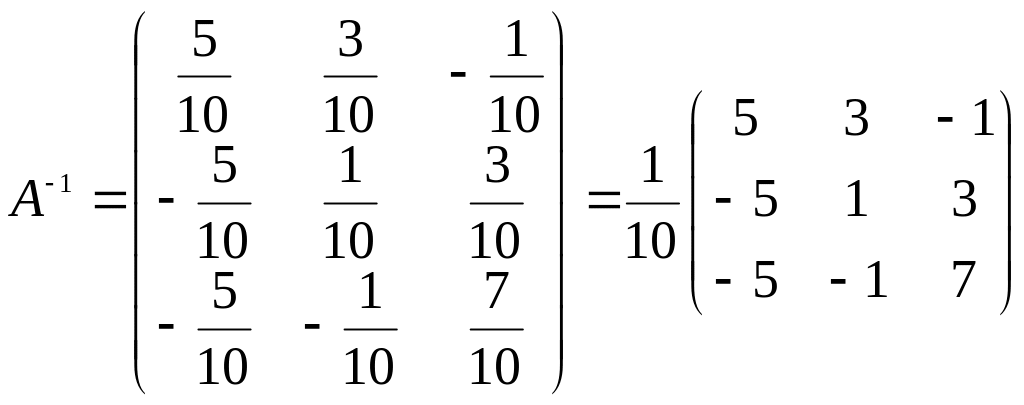 .
.
По формуле (2) находим решение данной системы уравнений в матричной форме:
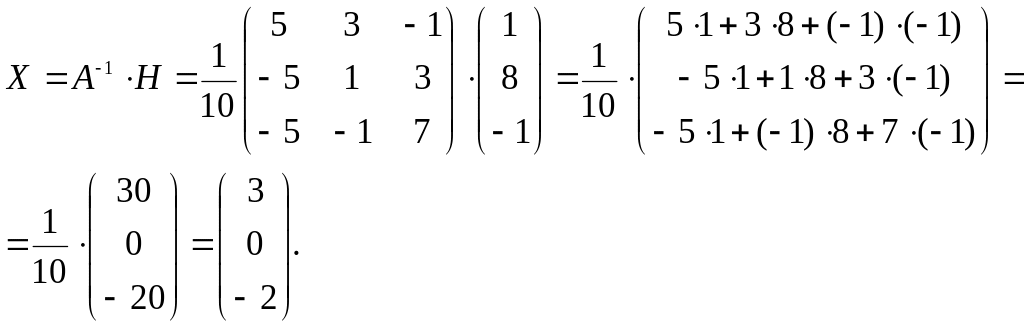
Отсюда
![]()
Задача 7. Вычислить пределы:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Решение.
а) Подстановка предельного значения
аргумента
![]() приводит к неопределенному выражению
вида
приводит к неопределенному выражению
вида
![]() .
.
Для
устранения этой неопределенности
разложим числитель и знаменатель дроби
на множители и сократим дробь на множитель
![]() .
Такое сокращение возможно, так как
множитель
отличен от нуля при
.
Такое сокращение возможно, так как
множитель
отличен от нуля при
![]() :
:
![]()
б)
При
![]() выражение
выражение
![]() дает неопределенность вида
дает неопределенность вида
![]() .
Для ее устранения умножим и разделим
это выражение на
.
Для ее устранения умножим и разделим
это выражение на
![]() :
:

в)
Обозначим
![]() .
Тогда
.
Тогда
![]() и
и
![]() при
при
![]() .
Применяя свойства пределов и формулу
первого замечательного предела
.
Применяя свойства пределов и формулу
первого замечательного предела
![]() ,
имеем:
,
имеем:
![]()
г)
При
выражение
![]() является неопределенностью вида
является неопределенностью вида
![]() .
Для устранения этой неопределенности
представим основание степени в виде
суммы 1 и бесконечно малой при
величины и применим формулу второго
замечательного предела:
.
Для устранения этой неопределенности
представим основание степени в виде
суммы 1 и бесконечно малой при
величины и применим формулу второго
замечательного предела:
![]() .
.
Тогда имеем:
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]() и
и
![]() при
.
Переходя к переменной у,
получим:
при
.
Переходя к переменной у,
получим:
![]() .
.
Справочные формулы Определители
1.
Определителем
2-го порядка
называется число, вычисляемое по формуле
![]()
![]() ,
где аij
называется элементом определителя;
первый индекс i
указывает номер строки, а второй индекс
j
– номер столбца.
,
где аij
называется элементом определителя;
первый индекс i
указывает номер строки, а второй индекс
j
– номер столбца.
2. Определителем 3-го порядка называется число, вычисляемое по формуле (правило треугольников)
 а11 а12 а13
а11 а12 а13
а21 а22 а23 = а11 а22 а33 + а21 а32 а13 + а12 а23 а31 – а31 а22 а13 – а21 а12 а33 –
а31 а32 а33
-а32 а23 а11 .
3. Минором Мij
элемента аij
определителя
![]() называется определитель, полученный
из данного путем вычеркивания элементов
i-ой строки и j-го
столбца (на пересечении которых находится
элемент аij).
называется определитель, полученный
из данного путем вычеркивания элементов
i-ой строки и j-го
столбца (на пересечении которых находится
элемент аij).
4. Алгебраическим дополнением Аij элемента аij данного определителя называется минор этого элемента, взятый со знаком (–1) i+j, т.е. Аij = (–1) i+j· Мij.
аi1
Аi1+
аi2
Аi2
+ …+ аin
Аin =
![]() (разложение по элементам i-й
строки, i = 1, 2,…, n);
(разложение по элементам i-й
строки, i = 1, 2,…, n);
а1j
А1 j
+ а2 j
А2 j
+ …+ аnj
Аnj =
![]() (разложение
по элементам j-го
столбца, j= 1,2,..,n).
(разложение
по элементам j-го
столбца, j= 1,2,..,n).
Свойства определителей
Замена всех строк соответствующими столбцами (транспонирование) не меняет значение определителя.
В дальнейшем строку или столбец будем называть рядом определителя.
Перестановка двух параллельных рядов меняет знак определителя.
Общий множитель всех элементов какого-нибудь ряда можно выносить за знак определителя.
Если все элементы какого-нибудь ряда равны нулю, то определитель равен нулю.
Определитель с двумя пропорциональными (равными) параллельными рядами равен нулю.
Сумма произведений элементов какого-нибудь ряда на алгебраические дополнения элементов параллельного ряда равна нулю.
Определитель не изменится, если к элементам какого-нибудь ряда прибавить элементы параллельного ряда, предварительно умноженные на одно и то же число.
Матрицы, операции над ними
1. Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Числа, составляющие матрицу, будем называть элементами матрицы аij, где i – номер строки, j – номер столбца или, в сокращенной записи, А=(аij); i = 1, 2,…, m; j = 1, 2,…, n.
Виды матриц
Матрица, состоящая из одной строки, называется матрицей-строкой (вектором-строкой), а из одного столбца – матрицей-столбцом (вектором-столбцом):
А = (а11; а12, …, а1n) – матрица-строка;

 1
n
1
n
b11
В = b21 – матрица-столбец
mx1 …
bm1
Матрица называется квадратной, если число ее строк равно числу столбцов.
Квадратная матрица А называется невырожденной, если

 0.
0.Квадратная матрица называется диагональной, если все ее недиагональные элементы равны нулю.
Диагональная матрица называется единичной, если все диагональные элементы равны единице, и обозначается Е.
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю, и обозначается (0).
Матрица А называется треугольной (ступенчатой, если m n), если ниже ее главной диагонали все элементы равны нулю.
Операции над матрицами
1
В = ·А
![]() bij
= аij
bij
= аij
где i = 1, 2,…, m; j = 1, 2,…, n.
2. Суммой двух матриц А и В одинакового размера mxn называется матрица С, элементы которой cij = аij+ bij, т.е.
С = А+В
cij
= аij+ bij
где i = 1, 2,…, m; j = 1, 2,…, n;
причем А+В = В+А; (А+В)+С = А+(В+С); (А+В) = А+В.
3. Разность двух матриц одинакового размера определяется через предыдущие операции: А – В = А + (–1)·В
4. Произведением матрицы А размера (mxk) на матрицу В размера (kxn) называется матрица С размера (mxn), элемент которой
сij
=
![]() аisbsj
, для i = 1, 2,…, m;
j = 1, 2,…, n;
т.е.
аisbsj
, для i = 1, 2,…, m;
j = 1, 2,…, n;
т.е.
А·В
= С
cij
= аi1b1j
+ аi2b2j+…+
аiкbкj mk
kn
mn
Свойства умножения матриц
А·В В·А – (в общем случае)
(А·В)·С = А·(В·С) – сочетательный закон.
(А·В) = (А) В = А·(В)
А·(В+С) = А·В + А·С
5) А·Е = Е·А = А,
г де
Е – единичная матрица того же
размера, что и матрица А.
де
Е – единичная матрица того же
размера, что и матрица А.
6) Если С = А·В, то С = А· В , где А и В квадратные матрицы.
5. Целой положительной степенью Аm (m>1) квадратной матрицы А называется произведение m матриц, равных А, т.е. Аm = А·А·…·А
m раз
6. Транспонирование матрицы – переход от матрицы А к матрице АТ, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица АТ называется транспонированной относительно матрицы А.
Матрица А -1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица, т.е. А-1·А = А·А-1 = Е.
