Различные постановки задачи Коши
ОДУ первого порядка, разрешённое относительно производной
Система n ОДУ первого порядка, разрешённая относительно производных (нормальная система n-го порядка)
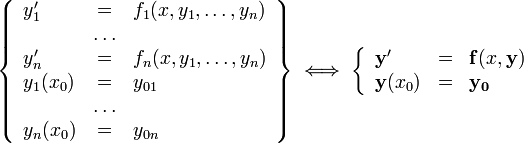
ОДУ n-го порядка, разрешённое относительно старшей производной
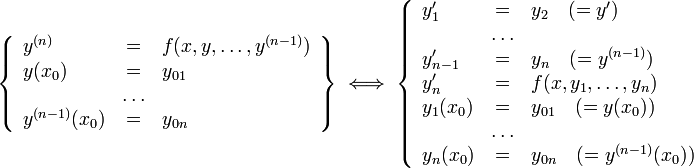
Теоремы о разрешимости задачи Коши для оду
Пусть
в области 
рассматривается
задача Коши:
где 
.
Пусть правая часть является непрерывной
функцией в 
.
В этих предположениях имеет место
теорема Пеано,
устанавливающая локальную разрешимость
задачи Коши: Пусть a>0 и b>0 таковы, что
замкнутый прямоугольник
принадлежит
области D, тогда на отрезке [x0 −
α,x0 +
α], где α
= min{a,b / M}, 
,
существует решение задачи Коши.
Указанный
отрезок называется отрезком Пеано.
Заметим, что, локальный характер теоремы
Пеано не зависит от гладкости правой
части. Например, для f(x,y)
= y2 +
1 и
для x0 =
0,y0 =
0 решение y(x)
= tan(x) существует
лишь на интервале (
− π,π). Также
отметим, что без дополнительных
предположений относительно гладкости
правой части, нельзя гарантировать
единственность решения задачи Коши.
Например, для 
возможно
более одного решения.
Чтобы сформулировать теорему о единственности решения задачи Коши, необходимо наложить дополнительные ограничения на правую часть. Будем говорить, что функция f(x,y) удоволетворяет условию Липшица на D относительно y, если существует постоянная L такая, что
для
всех 
,
i=1,2.
Пусть правая часть f(x,y) дополнительно удовлетворяет условию Липшица на D относительно y, тогда задача Коши не может иметь в D более одного решения.
Также отметим, что хотя эта теорема имеет глобальный характер, тем не менее она не устанавливает существование глобального решения.
Для существования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию
где A>0 - константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D. В частности, из этой теоремы следует, что задача Коши для линейных уравнений (с непрерывными по x коэффициентами) имеет глобальное решение.
Метод исключения — сведение системы ду к одному уравнению
Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.
Введением новых функций
это
уравнение заменяется нормальной
системой 
уравнений
Можно утверждать и обратное, что, вообще говоря, нормальная система уравнений первого порядка эквивалентна одному уравнению порядка . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения. Проиллюстрируем этот метод на примере системы двух уравнений:
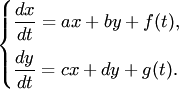(1)
Здесь 
—
постоянные коэффициенты, а 
и 
—
заданные функции; 
и 
—
искомые функции. Из первого уравнения
системы (1) находим
(2)
Подставляя
во второе уравнение системы вместо у
правую часть (2), а вместо 
производную
от правой части (2), получаем уравнение
at второго порядка относительно
где 
—
постоянные. Отсюда находим 
.
Подставив найденное выражение для 
и 
в
(2), найдем 
.
Пример 1. Проинтегрировать систему уравнений
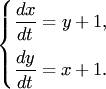(3)
Решение. Из
первого уравнения системы (3) находим 
,
тогда
(4)
Подставляя (4) во второе уравнение системы (3), получаем линейное дифференциальное уравнение с постоянными коэффициентами второго порядка
(5)
Общее решение уравнения (5)
(6)
Находя
производную по 
от
(6), получаем
Общее решение системы (3):
Пример 2. Решить задачу Коши для системы
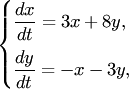(7)
(8)
Решение. Из второго уравнения системы (7) находим
(9)
откуда
(10)
Подставляя
(9) и (10) в первое уравнение системы (7),
получаем уравнение 
,
общее решение которого
(11)
Подставляя
(11) в (9), найдем 
.
Общее решение системы (7)
(12)
При
начальных условиях (8) из (12) получим
систему уравнений для определения 
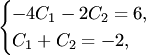
решая
которую, найдем 
.
Подставляя эти значения 
и 
в
(12), получаем решение поставленной задачи
Коши:
