12. Теорема – необходимое условие линейной независимости решений линейного однородного дифференциального уравнения.

 α₁, α₂, …, α_n   (a < x < b)       (1)

 Дадим признак линейной независимости n частных решений (1) однородного линейного уравнения n-го порядка. С этой целью введем в рассмотрение определитель, составленный из данных частных решений и их производных до порядка n – 1 включительно:

            W(x) = 

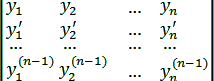
   Этот определитель называется определителем Вронского решений y₁, y₂, …, y_n.

   Теорема. Для того чтобы решения (1) были линейно независимы в (a, b), т. е. в интервале непрерывности коэффициентов уравненияL(y) = 0, необходимо и достаточно, чтобы W(x) не обращался в нуль ни в одной точке из (a, b).

   Значение определителя Вронского n решений однородного линейного уравнения L(y) = 0 тесно связано с самим уравнением, а именно: имеет место следующая формула Остроградского—Лиувилля:

            W(x) = W(x₀)  .       (2)

   Из формулы (2) видно, что определитель Вронского n решений уравнения L(y) = 0 обладает двумя замечательными свойствами:

Если W(x) обращается в нуль в одной точке из интервала (a, b), то он равен нулю во всех точках этого интервала.

Если W(x) не равен нулю в одной точке из интервала (a, b), то он отличен от нуля во всех точках этого интервала.

   Таким образом, для того, чтобы n решений (1) составляли фундаментальную систему решений уравнения L(y) = 0 в интервале (a, b), достаточно, чтобы их определитель Вронского был отличен от нуля в одной точке x₀ ∈ (a, b).

13.Теорема о структуре общего решения линейного однородного дифференциального уравнения.

Если y₁, y₂,… y_n есть линейно независимые решения линейного однородного дифференциального уравнения, то

y = c₁ y₁ + c₂ y₂ + … + c_n y_n                      (1)

есть общее решение этого уравнения.    Доказательство. Покажем, что можно найти такие постоянные c₁, c₂, … , c_n , что функция (1) будет удовлетворять заданным начальным условиям

Удовлетворяя начальным условиям, приходим к системе алгебраических уравнений относительно c₁, c₂, … , c_n

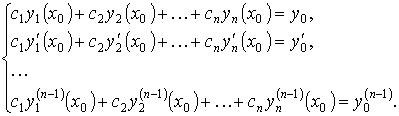
Так как главный определитель этой системы равен определителю Вронского, который не равен нулю, то эта система имеет единственное решение. Что и требовалось доказать.

14.Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.

Общее решение линейного неоднородного дифференциального уравнения с непрерывными на интервале (a, b) коэффициентами и правой частью

Ln(y) =  ;

(1)

равно сумме общего решения соответствующего однородного уравнения

Ln(y) =  ;

(2)

и частного решения неоднородного уравнения (1): y_он(x) = y_оо(x) + y_чн(x) = (C₁ y₁(x) + C₂ y₂(x) + …+ C_n y_n(x)) + y_чн(x).  Док-во. Мы должны доказать, что если известно частное решение y_чн(x) неоднородного уравнения (1), то любое его другое частное решение   может быть получено по формуле   при некотором наборе постоянных C₁, C₂, …, C_n. Так как и y_чн(x), и   - решения неоднородного уравнения (1), то L_n(y_чн(x)) = f(x) и  , следовательно, по линейности оператора L_n(y),  . Функция  удовлетворяет однородному уравнению, поэтому содержится в формуле C₁ y₁(x) + C₂ y₂(x) + …+ C_n y_n(x) при некотором наборе постоянных C₁, C₂, …, C_n:  . Таким образом,  , что и требовалось доказать.  Из предыдущей теоремы следует, что для нахождения общего решения линейного неоднородного дифференциального уравнения необходимо знать его частное решение. Здесь мы сформулируем и докажем теорему, которая позволяет свести нахождение частного решения неоднородного уравнения с правой частью вида   (  - постоянные) к, возможно, более простой задаче нахождению частных решений этого уравнения с правыми частями вида f(x) = f₁(x), f(x)=f₂(x)