Тема 3 Алгоритмически неразрешимые проблемы

Разделяют проблемы одиночные и массовые.

Например:

5+7=? – одиночная проблема.

х+у=? – массовая проблема.

Принципиально неразрешимыми должны быть алгоритмы получения объектов, которые парадоксальны, или решения задач, из которых вытекало бы существование парадоксальных объектов.

Например, парадоксами являются:

1) 5-ая аксиома Евклида (Лобачевский дал ей опровержение).

2) 2*2=5

Пример 1:

10-ая проблема Гильберта.

Д. Гильберт в 1901 г. при решении диофантовых уравнений выдвинул проблему, которая гласит:

Найти алгоритм, определяющий некоторое целочисленное решение для произвольного диофантового уравнения

F(x, y, …)=0

Это – полином с целыми показателями степеней и целыми коэффициентами при неизвестных

a_nxⁿ+a_n-1x^n-1+…+a₂x²+a₁x+a₀=0

Для приведенного уравнения существует частное решение, которое заключается в том, что всякий целочисленный корень x_i является делителем a₀. При этом a₀ раскладывают на простые множители и проверяют каждый множитель на соответствие корню.

В 1970 г. ленинградский математик Ю. Матиясевич математически доказал алгоритмическую невозможность решения диофантового уравнения в общем виде.

Пример 2:

Теорема Ферма:

Не существует таких целых чисел a, b, с, n (n>2), для которых справедливо равенство

aⁿ + bⁿ = cⁿ

Эта теорема была доказана для многих значений n и проверена для частных случаев, однако до сих пор не создано общее доказательство теоремы.

Пример 3:

Проблема Гольдбаха.

Х. Гольбах в 1742 г. в письме к Эйлеру сформулировал проблему:

Доказать, что каждое целое число N6 может быть представлено в виде суммы трех простых чисел

N=a+b+c

Это значит, что нужно найти алгоритм, который позволил бы для любого целого числа N6 найти хотя бы одно разложение на три простых слагаемых.

Частый случай решения этой проблемы предложил Эйлер: для четных N эта проблема разрешима и равносильна разложению на два простых слагаемых.

И. Виноградов в 1937 г. доказал, что для нечетных N можно найти три простых слагаемых, но для четных чисел решение не найдено до сих пор.

Тема 4 Классы p- (polynomial) и np- (nondeterminated polynomial) задач.

4.1 Понятие р- и np-задач.

В зависимости от значений функции f(N) различают следующие классы алгоритмов:

1) Задачи, для которых

f(N)=aN (линейная сложность)

Примеры: топологическая сортировка, отыскание остовного дерева и связанных компонент дерева.

2) Задачи, для которых f(N) является нелинейной, но не более чем полиномиальной

f(N)=N^m, m2

Примеры: умножение матриц, нахождение кратчайшего пути в дереве, нахождение минимума остовных деревьев.

3) Задачи, о которых нельзя сказать, что они обязательно имеют экспоненциальную сложность, но для которых не известны быстрые алгоритмы, требующие менее, чем kⁿ операций.

Примеры: задача коммивояжера (TSP), определение изоморфизма, алгоритм нахождения максимальной клики в графе.

4) Задачи с обязательной экспоненциальной сложностью

f(N)=K^N , K2

Для этого класса не существует быстрых алгоритмов.

Примеры: прохождение всех остовных деревьев графа, всех его циклов и всех клик.

Для таких задач невозможно открыть новый алгоритм с меньшей сложностью.

Замечание: Для 3-го класса задач существуют теоретические предпосылки разработки эффективных алгоритмов с полиномиальной сложностью (класса 2), но которые пока не найдены. Разработка полиномиального алгоритма для любой из задач 3-го класса автоматически означала бы решение всех задач этого класса за полиномиальное время.

Полиномиальный алгоритм – это алгоритм с полиномиальной трудоемкостью (временем работы).

Полиномиальный или экспоненциальный характер работы алгоритма инвариантен относительно формы представления входных данных (двоичная, десятичная или другая система счисления).

Говорят, что алгоритм является полиномиальным, если время его работы, т. е. временная сложность, ограничивается сверху полиномом некоторой степени T(N)=O(N^m). Тогда все задачи, которые решаются таким алгоритмом, образуют Р-класс задач. Говорят, что эти задачи входят в Р.

Задачи, временная сложность которых экспоненциальна (T(N)=O(K^N)), не входят в Р.

Замечание: Можно показать, что задачи с линейной сложностью входят в Р

T(N)=O(N¹)

Введем класс NP-задач, которые можно решить за полиномиальное время с помощью недетерминированного алгоритма.

Определим состояние алгоритма как совокупность адреса выполняемой в данный момент команды и значений всех переменных, что эквивалентно вектору состояния процесса. Поэтому большинство алгоритмов являются детерминированными, т. е. в них для любого состояния существует лишь одно допустимое следующее состояние (включая операции условия и выбора). Это значит, что такой алгоритм в каждый момент времени может делать что-то одно.

В недетерминированном алгоритме (НДА) для любого данного состояния может быть больше одного допустимого следующего состояния, т. е. такой алгоритм в каждый момент времени может выполнить больше одного оператора.

НДА не является случайным или вероятностным алгоритмом. Он представляет собой алгоритм, который может находиться во многих состояниях (это эквивалентно параллельному решению задачи с множеством вариантов).

Пример:

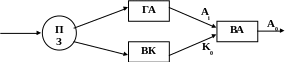
Детерминированный алгоритм (ДА) решал бы эту задачу последовательно (перебор всех вариантов, сравнение с критерием оптимальности K₀ до тех пор, пока не выберет альтернативу А₀).

НДА может одновременно (параллельно) получить все альтернативы и сравнить с K₀, копируя самого себя в виде отдельного процесса для каждой альтернативы, которая выполняется независимо.

При этом если какая-либо копия обнаружит, что получен неправильный результат или результат не получен, то она прекращает свое исполнение. Если же копия находит решение, удовлетворяющее K₀, то она объявляет об успехе, и все другие копии прекращают работу.

Т. о. НДА характеризуется тремя параметрами:

1. выбор – многозначная функция, значения которой являются элементами множества S;

2. неудача заставляет копию алгоритма прекратить работу;

3. успех заставляет все копии алгоритма прекратить работу и сформировать результат.

Очевидно, что никакое физическое устройство не способно на неограниченное недетерминированное поведение, значит, НДА является теоретическим методом.

Задачи, которые можно решить с помощью полиномиального НДА, образуют класс NP-задач.

4.2 NP-трудные и NP-полные задачи.

Задача, входящая в Р, является NP-трудной, если существует полиномиальный ДА (ПДА) ее решения, который модно использовать для получения решения всех задач, входящих в NP. Т. е. такая задача является NP-трудной, если она, по крайней мере, так же трудна, как любая задача, входящая в NP.

NP-трудная задача, принадлежащая NP, называется NP-полной задачей. Такие задачи не менее трудны, чем любая задача из NP. При этом существование ПДА для NP-трудной или NP-полной задачи означает, что классы Р и NP совпадают, т. е. возможно решение всех задач 3-го класса быстрым алгоритмом.

Для доказательства того, что задача является NP-трудной, необходимо показать, что если для задачи существует ПДА, то его можно использовать для получения другого ПДА решения задач, входящих в NP.

Чтобы установить, что задача является NP-полной, необходимо доказать, что она принадлежит NP.

Идея использовать алгоритм решения одной задачи для получения алгоритма решения другой является одной из наиболее важных в теории алгоритмов.

Определение 1: Задача Р1 преобразуется в задачу Р2, если любой частный случай задачи Р1 можно преобразовать за полиномиальное время в некоторый частный случай задачи Р2. Тогда решение Р1 можно получить за полиномиальное время из решения частного случая задачи Р2.

Если Р1Р2 и Р2Р, то и Р1Р.

Определение 2: Задача является NP-трудной, если каждая задача, входящая в NP, преобразуется в нее. Задача является NP-полной, если она является одновременно NP-трудной и принадлежит NP.