1.10 Сложность алгоритмов.

Временная сложность алгоритма (T(N), где N – размер задачи) – это время выполнения алгоритма, измеренное в шагах (инструкциях алгоритма, которые нужно выполнять для достижения результата). Т. е. это – число элементарных операций, из которых складывается алгоритм решения задачи (:=, <>, =, +, –, *, /; and, or, not, xor; call, return).

Различают три разновидности временной сложности, которые зависят от комбинации входных данных при решении задачи (равнозначность, разряженность, упорядоченность и др. свойства входных данных).

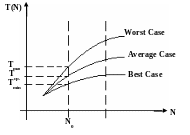
Worst Case – максимальное время выполнения (наихудший возможный случай).

Average Case – среднее время выполнения (в статистическом смысле).

Best Case – минимальное время (наилучший случай).

На практике оперируют максимальным временем выполнения алгоритма.

Пример 1:

Сложность алгоритма умножения матрицы на вектор порядка N может быть записана:

Случай T(N)=C*N² применим для квадратной матрицы.

Элементарные операции в данном случае – совокупность «+» и «*».

Если исходная матрица – единичная, то получаем Best Case.

Если в матрице половина элементов – 0, половина – 1, то получаем Average Case.

Константа С, которая не может быть точно выражена, характеризует влияние внешних факторов на время выполнения алгоритмов (быстродействие ЭВМ, скорость компиляции). Поэтому использование единиц времени для оценки временной сложности алгоритмов не совсем корректно. В этом случае говорят, что временная сложность алгоритма умножения матрицы на вектор пропорциональна N².

Характер поведения временной сложности при увеличении N (N) называется асимптотической сложностью алгоритма.

Для описания скорости роста асимптотической сложности используется О-нотация. Когда говорят, что временная сложность алгоритма имеет порядок N²:

T(N)=O(N²)=O(f(N)),

То подразумевается, что существуют положительные константы C, n₀=const (C>0), такие, что для всех N  N₀ выполняется неравенство

T(N)  C*f(N)

(1)

Это – верхняя граница оценки сложности.

Пример 2:

Пусть Т(0)=1, Т(1)=4, …, Т(N)=(N+1)_­­­­², тогда временная сложность этого алгоритма имеет порядок роста T(N)=O(N²).

Можно показать, что для всех N > n₀ при n₀ = 1, C = 4 выполняется неравенство (1).

(N+1)²  4*N²

Пример 3:

Если временная сложность записывается в виде полинома

T(N)=C₁N²+C₂N+C₃,

то такой алгоритм имеет порядок сложности, кратный степени максимального элемента полинома, т. к. он растет наиболее быстро при N:

T(N)=O(N²).

Например:

3n²+5n+1  5n²

 n  1

Пример 4:

Если некоторый алгоритм имеет сложность, кратную 3ⁿ, тогда можно показать, что порядок роста скорости не может быть кратен O(2ⁿ):

T(N)=3ⁿ O(2ⁿ).

Пусть существуют константы C, n₀, такие, что выполняются неравенство:

3­­­­­ⁿ  C*2ⁿ, n  n₀.

Отсюда получаем:

С  (3/2)², n  n₀.

Но при n не существует такой константы С, которая удовлетворяла бы данному неравенству.

Кроме верхней границы сложности существует и нижняя граница скорости роста временной сложности:

T(N)  (f(N))

(2)

Неравенство (2) подразумевает, что существует некоторая константа С, для которой при N временная сложность

T(N)  C*f(N).

Учитывая сложность точного определения T(N) (асимптотической временной сложности), в зависимости от размеров исходных данных на практике используют нижние и верхние границы временной сложности алгоритма:



T(N) = (f(N))

В зависимости от значения константы С скорость роста сложности алгоритма может существенно меняться.

Пример 5:

Пусть временная сложность записывается формулой

T(N)=3n² –100n+6=O(n²)

3n² >3n² –100n+6, n1, C=3.

Если С₁0 (С₁=0,00001), тогда неравенство

10^-5n² > 3n² –100n+6, n1

не выполняется.

Но можно показать, что порядок роста сложности

3n² –100n+6  O(N).

C*N < 3N², N>C.

3n² –100n+6=(n²)

C=2.29, n  n_0.

2.99*n² < 3n² –100n+6