Тема 5. Методы разработки алгоритмов.
Существует достаточно большое число методов разработки эффективных алгоритмов решения задач различных классов.
Наиболее часто используются следующие методы:
«Разделяй и властвуй» - метод декомпозиции, метод сведения задачи к подзадачам, метод частных целей.
Балансировка. Этот метод применим только к алгоритмам, к которым уже применялся 1-ый метод.
Динамическое программирование.
«Жадный» алгоритм.
Метод программирования «с отходом назад» (Back Tracing), программирование с отслеживанием.
Метод локального поиска.
Метод подъема.
Метод эвристики.
Метод рекурсии.
Моделирование задач.
5.1 Метод «Разделяй и властвуй».
При решении задачи необходимо ответить на следующие вопросы:
Известно ли решение для какой-либо части задачи и можно ли решить оставшуюся неизвестной часть.
Известны ли частные случаи решения задачи, и можно ли разработать алгоритм решения задачи для ограниченного подмножества исходных операндов.
Существует ли в задаче неясные моменты (раскрытие глубины задачи).
Существует ил похожая задача того же класса и решение для нее. Можно ли изменить алгоритм решения второй задачи для получения решения первой.
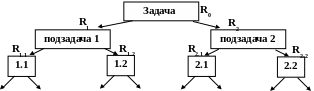
В основе метода «Разделяй и властвуй» лежит разбиение задачи на подзадачи (декомпозиция).
Первый шаг – это разделение задачи на К подзадач со сложностью 1/К.
Властвование – второй шаг алгоритма. Это – использование рекурсионного процесса разбиения подзадач на еще более мелкие подзадачи до тех пор, пока подзадачи n-го уровня разделения будут достаточно малы для их тривиального решения.
… … … …
Третий этап метода – склеивание множества решений отдельных подзадач в общее решение.
Использование этого метода требует, чтобы в процессе разбиения подзадачи не повторялись и не пересекались друг с другом. Если это условие не выполняется, то данный метод решения не применим к таким задачам.
Примерами решаемых этим методом задач являются:
сортировка слиянием;
нахождение максимального/минимального элемента массива;
умножение длинных целочисленных значений;
алгоритм быстрого преобразования Фурье;
алгоритм «Ханойская башня»;
составление графика проведения чемпионата.
Задача 5.1.1
Отсортировать массив из n чисел в порядке возрастания.
Обменная сортировка:
-
6
3
2
7
5
1
3
7
-
1
3
2
7
5
6
3
7
-
1
2
3
7
5
6
3
7
-
1
2
3
3
5
6
7
7
1 итерация
2 итерация
3 итерация
Общая формула временной сложности записывается рекуррентно:
T(n)=n*(n-1)/2=O(n2)
Приведенный алгоритм построен на основе метода «Разделяй и властвуй».
Недостаток: в приведенном алгоритме размеры подзадач на каждой итерации одинаковы, поэтому при больших n этот алгоритм неэффективен.
Для повышения эффективности алгоритмов, разработанных методом «Разделяй и властвуй», используется метод балансировки, который заключается в разбиении задачи на подзадачи равных размеров.
Например:
Алгоритм сортировки слиянием.
-
6
3
2
7
5
1
3
7
-
3
6
2
7
1
5
3
7
-
2
3
6
7
1
3
5
7
-
1
2
3
3
5
6
7
7
Вычислительная сложность этого алгоритма:
T2(n)=O(n*log(n)),
поэтому можно сделать вывод, что данный алгоритм также является рекурсивным.
Пример процедуры, реализующей этот алгоритм:
Procedure JointSort(P, R: integer;
var A, B: TArray);
var q: integer;
begin
if P=R then exit;
q:= (P+R) div2;
JointSort(P, q, A, B);
JointSort(q+1, R, B, A);
JointSort(P, q, R, B, A);
end;
Метод «Разделяй и властвуй» полезен, если задачу можно разбить на подзадачи за приемлемое время, а суммарный размер подзадач будет небольшим.
Если сумма размеров подзадач пропорциональна a*N, где а=const (a>1), то этот метод дает алгоритм с полиномиальной сложностью O(Nm).
Если разбиение задачи размером N приводит к N подзадачам, каждая из которых имеет сложность (N-1), то такой алгоритм будет иметь экспоненциальную сложность O(mN).
Задача 5.1.2
Составление сетевого графика выполнения работ.
Имеется комплекс взаимосвязанных работ N. Для каждой из работ задана трудоемкость выполнения. Имеется К рабочих. Требуется распределить рабочих по операциям таким образом, чтобы длительность выполнения всего комплекса работ была минимальной.
Примечание: не учитываются субъективные факторы, и невозможно перемещение рабочих с одной операции на другую в процессе выполнения.
Комплекс взаимосвязанных работ представляется в виде сетевого графика, где узлы графа – это события окончания предшествующих работ, дуги – работы.
Трудоемкость Ri,j характеризует затраты ресурсов на выполнение работы.
Пример сетевого графика:
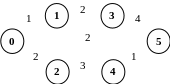
L(0, М) – длительность выполнения работы. Эта величина определяется как совокупность возможных путей в графе
{I1, I2, I3}
В данном примере возможны 3 маршрута:
I1={(0, 1); (1, 3); (3, 5)}
I2={(0, 1); (1, 4); (4, 5)}
I3={(0, 2); (2, 4); (4, 5)}
I1=1+2+4=7 – «критический» путь Iкр.
I2=1+2+1=4
I1=2+3+1=6
Необходимо расставить по операциям заданное число рабочих.
Для случая, когда K=N задача является тривиальной.
Для KN имеется N(K-N) возможных вариантов расстановки.
Пусть N=7, К=10, тогда имеется 1296 вариантов размещения рабочих.
Решение этой задачи методом полного перебора вариантов неэффективно.
Используя метод «Разделяй и властвуй», разбивают исходную задачу на (К-N) последовательных подзадач. Затем решают вопрос о том, на какую операцию поставить 1-го свободного рабочего (для данного примера – 8-го рабочего). После этого размещают 2-го свободного рабочего, взяв за исходное ранее найденное решение и т.д.
Каждая из этих подзадач может быть сформулирована следующим образом: необходимо принять решение о добавлении одного работника на одну из работ комплекса, чтобы полученная расстановка минимизировала «критический» путь
Свободного рабочего размещают на одну из работ, входящих в «критический» путь, желательно, наиболее трудоемкую (здесь – (3, 5)).
Тогда получаем:
I1’=1+2+4/2=5 I3=6 Iкр
L(0, 5)=6
Поиск решения данным алгоритмом требует анализа не более N*(K-N) вариантов.