5.9 Методы имитационного моделирования.

Ряд задач теории алгоритмов связан с описанием работы больших систем. Для таких задач сложно построить точный алгоритм, т. к. трудно определить все переменные, влияющие на поведение системы и внутренние связи между ними.

Обычно неизвестно распределение вероятностей случайных переменных, а функции системы являются непрерывными.

Имитационное моделирование (ИМ) – это процесс вычислительного эксперимента над динамической моделью системы.

Конечной целью ИМ является:

• формирование стратегии управления;

• определение оптимальных конфигураций системы;

• установление реальных производственных планов;

• получение оптимальной экономической стратегии.

ИМ позволяет получить информацию о реальной системе, когда невозможно или нецелесообразно проводить реальные эксперименты.

Области применения ИМ включают задачи теории массового обслуживания. Самыми распространенными алгоритмами ИМ являются алгоритмы моделирования очередей.

Тема 6. Параллельные алгоритмы.

6.1 Понятие параллельных алгоритмов.

Объединение нескольких вычислительных систем в общую систему распределенной обработки данных позволяет реализовать эффективные алгоритмы решения трудных задач (с экспоненциальной, факториальной сложностью).

Если задачу нельзя решить с помощью последовательного алгоритма, разработанного одним из эффективных методов, то прибегают к распараллеливанию алгоритма с целью увеличения его быстродействия.

Примеры задач, в которых используется распараллеливание:

1. Одновременное выполнение операций ввода/вывода.

2. Формирование и обнуление массива.

3. Арифметические и логические операции над векторами и матрицами.

4. Одновременное отслеживание ветвей в различных узлах дерева.

5. Конвейерная обработка.

6. Решение СЛАУ большого порядка.

7. Параллельная сортировка.

8. Поиск максимума/минимума функции.

Сложность полученного параллельного алгоритма (ПА) дает выигрыш как минимум на порядок по сравнению с последовательным алгоритмом.

Сложность ПА оценивается гипотезой Минского: параллельные вычислительные системы, выполняющие последовательную программу под множеством исходных данных размера N, дают прирост производительности по крайней мере на показатель 1/log(N).

Однако при распараллеливании задач есть ряд «подводных камней»:

1) Во многих случаях ПА дает малый прирост производительности (быстродействия), поэтому проще применить эффективные методы построения быстрых последовательных алгоритмов для однопроцессорных универсальных ЭВМ, чем распараллеливать задачу для многопроцессорных специальных ЭВМ.

Кроме того, выбор средств разработки ПА весьма ограничен, а полученный параллельный код менее оптимизирован, чем для последовательных ЭВМ на этапе компиляции.

2) Быстрые последовательные алгоритмы во многих случаях дают более высокое быстродействие, чем ПА, построенные на основе прямого алгоритма решения задачи, а распараллеливание быстрого последовательного алгоритма является сложной задачей.

3) Для разработки ПА необходимо разбить задачу на независимые подзадачи с объединением результатов подзадач на последнем этапе. Этот процесс не поддается отладке, и быстродействие всего алгоритма сильно зависит от размеров подзадач и последнего этапа. В лучшем случае подзадачи должны быть маленьких и одинаковых размеров.

Пример 1:

П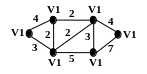 А отыскания минимального остовного дерева.

Если одновременно выбрать для каждой вершины связанное с ней ребро с минимальным весом, то в остовном дереве возникнут замкнутые циклы, а это недопустимо.

V1: (V1, V2)

V2: (V2, V4)

V3: (V3, V2)

V4: (V4, V1)

V5: (V5, V4)

V6: (V6, V2)

О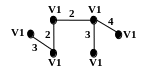 днако если выбрать для каждой вершины V_i ребро наименьшего веса, которое идентично вершине V_j (ji) с наименьшим индексом j, то исключается возможность циклов.

Это условие позволяет найти остовное дерево минимального веса за один шаг ПА. Однако при большом числе вершин рассмотренный алгоритм не настолько быстрый. Модификация этого алгоритма, предложенная Соллином, более эффективна. При этом сложность задачи уменьшается с O(N²) до O(log₂N).

Пример 2:

Задача сортировки массива из N целых чисел.

P_i –процессоры (i=1…N).

P₁ P₂ P₃ P₄ P₅ P₆ P₇ P₈

6

3

7

2

8

4

1

5

3

6

2

7

4

8

1

5

 

3

2

6

4

7

1

8

5

2

3

4

6

1

7

5

8

 

2

3

4

1

6

5

7

8

2

3

1

4

5

6

7

8

 

2

1

3

4

5

6

7

8

1

2

3

4

5

6

7

8

 

1

2

3

4

5

6

7

8

1

2

3

4

5

6

7

8

1) Шаг 1

2) Шаг 2

3) Шаг 1

4) Шаг 2

5) Шаг 1

6) Шаг 2

7) Шаг 1

8) Шаг 2

9) Шаг 1

Шаг 0: присваиваются исходные значения

M=0, t=0 (М – критерий остановки алгоритма).

Шаг 1: Do Through шаг 3

while M2

else Stop

Шаг 2: If t=четное Then сравнить (I_2k, I_2k-1) для (P_2k, P_2k-1),  K=1, 2, …, N/2

If I_2k<I_2k-1 then

I_2kP_2k-1

I_2k-1P_2k

Шаг 3: If была перестановка Then M=0

Else M=M+1

t=t+1

Этот алгоритм сортировки упорядочивает массив из N чисел за N+1 шагов в реальном масштабе времени, производя на каждой итерации N/2 операций сравнения, что требует время порядка O(N²).