5.6 Метод ветвей и границ.

Данный метод является разновидностью поиска с возвратом, поскольку исследует дерево решений и применяется для широкого класса дискретных комбинационных задач.

Если алгоритм поиска с возвратом направлен на поиск первого или всех решений для заданного N, то метод ветвей и границ направлен на оптимизацию решения (поиск максимального или минимального решения или в зависимости от критерия оптимальности).

В решаемой задаче задается целевая функция стоимости для любой из вершин дерева поиска с целью найти минимальную конфигурацию стоимости. Для задач коммивояжера такой алгоритм считался самым эффективным до 1970 года, когда были предложены эффективные алгоритмы направления эвристики. При этом эвристический алгоритм решения задачи можно использовать как качественное решение для задачи коммивояжера, решаемой алгоритмом ветвей и границ. Это дает на начальном этапе некоторое приближение к точному решению и сокращает пространство поиска в дереве.

1 этап: В матрице стоимости ищутся сначала минимальные элементы в каждой строке и производится вычитание.

S =

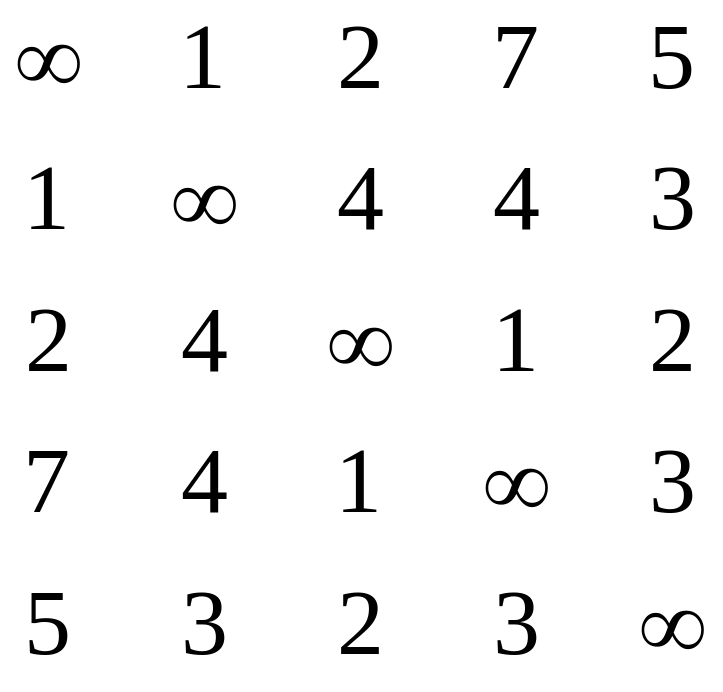
П олучаем:

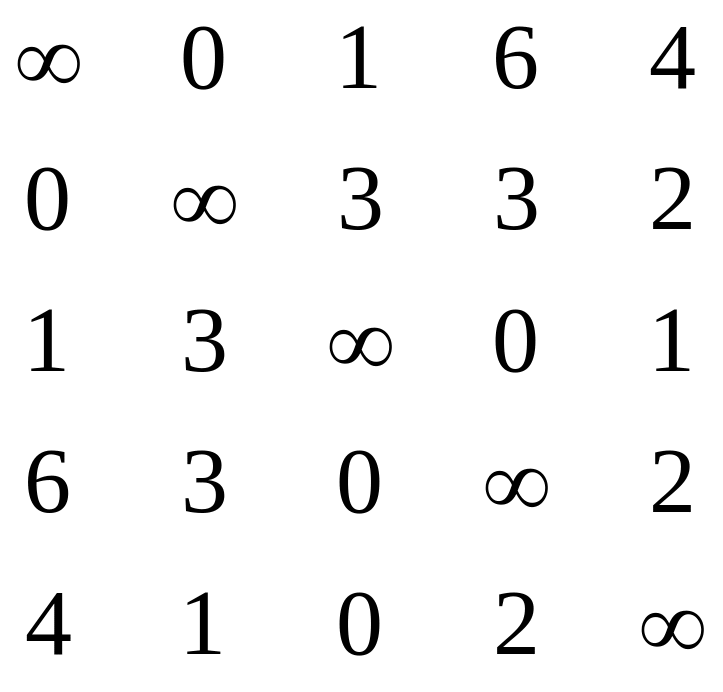
Запоминаем h₁= h₂= h₃= h₄=1, h₅=2

Затем производится поиск минимальных элементов в каждом столбце и снова производится вычитание:

h₆= h₇= h₈= h₉=0, h₁₀=1

П олучаем: 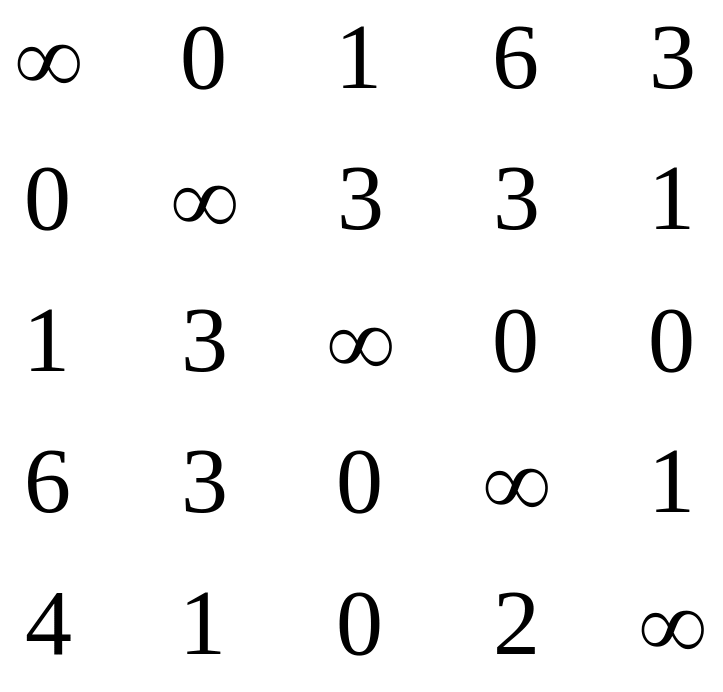= - приведенная матрица.

Определим сумму всех h_i:

H_i=

H_i является нижней границей стоимости каждого тура для данной вершины графа.

2 этап: В приведенной матрице находим базовый путь в результате поиска строки с номером i, имеющей не менее двух стоимостей, не равных . Среди набора элементов выбираем в качестве базы с наименьшим индексом.

После выбора базы приводим ветвления в графе, т. е. осуществляем построение двух матриц L и R.

Для нашего случая в качестве кандидатов на базовый элемент используются элементы приведенной матрицы R=0:

(S₁₂,, S₂₁, S₃₄,, S₃₅,, S₄₃,, S₅₃ )

среди них выбираем базовый элемент, имеющий максимальную сумму наименьших элементов в той же строке и столбце, что и кандидат.

Пример:

S₁₂=1+1=2

S₂₁=1+1=2

S₃₄=1

S₃₅=1

S₄₃=1

S₅₃=1

В качестве базы берем S₁₂, строим для него L и R.

L получается приравниванием к  всех элементов, стоящих в той же строке и в том же столбце, что и базовый элемент, а также асимметричный ему элемент по индексу.

Т. о. асимметричный базе элемент - S_21.

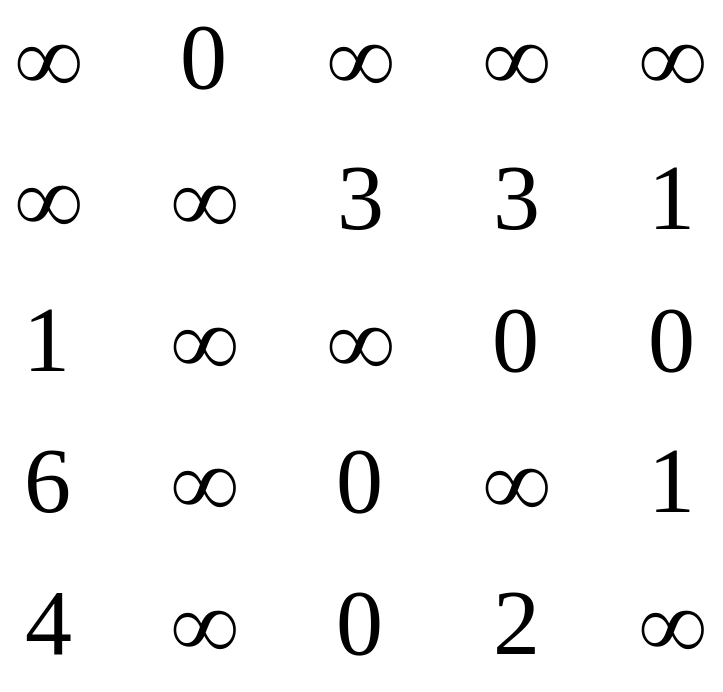- вершина L первого уровня.

Рассматриваем L₁ в качестве исходной, выполняем приведение и поиск базового элемента для получения матриц L₂ и R₂.

Результат:

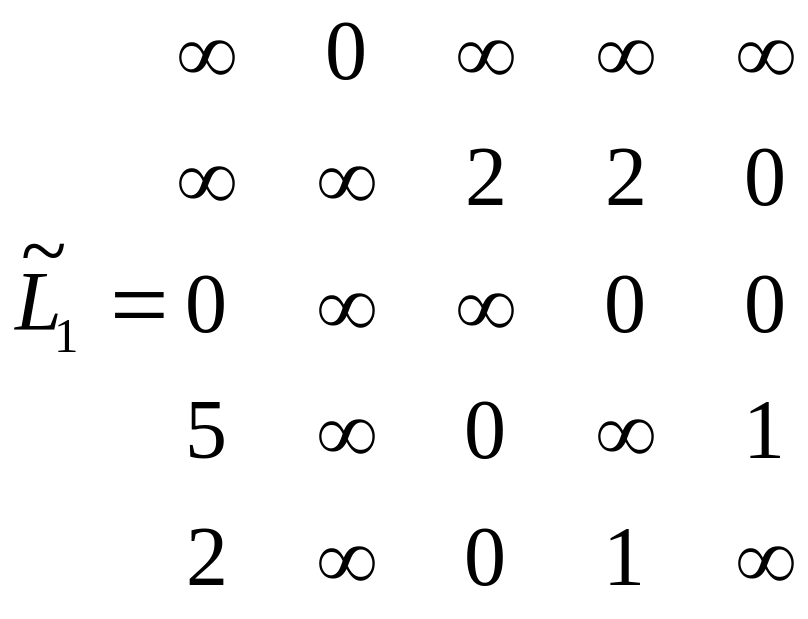
h₂₅=h₃₁=1

H₂=1+1=2

H₂=H₁+H₂=7+2=9

H₂ – нижняя граница стоимости каждого тура наследия этой вершины.

Получаем матрицы L₂ и R₂ описанным выше способом и повторяем этот процесс до тех пор, пока не будут достигнуты листья дерева.

Для листа дерева, соответствующего какому-либо туру, в матрице есть только один элемент в каждой строке и в каждом столбце, неравный .

(S₂₅,, S₃₁, S₃₄,, S₃₅,, S₄₃,, S₅₃ )

S₂₅ – база, S₅₂ - ; H₃=H₂+1=9+1=10

Т. о. листок дерева будет иметь вид:

L₅=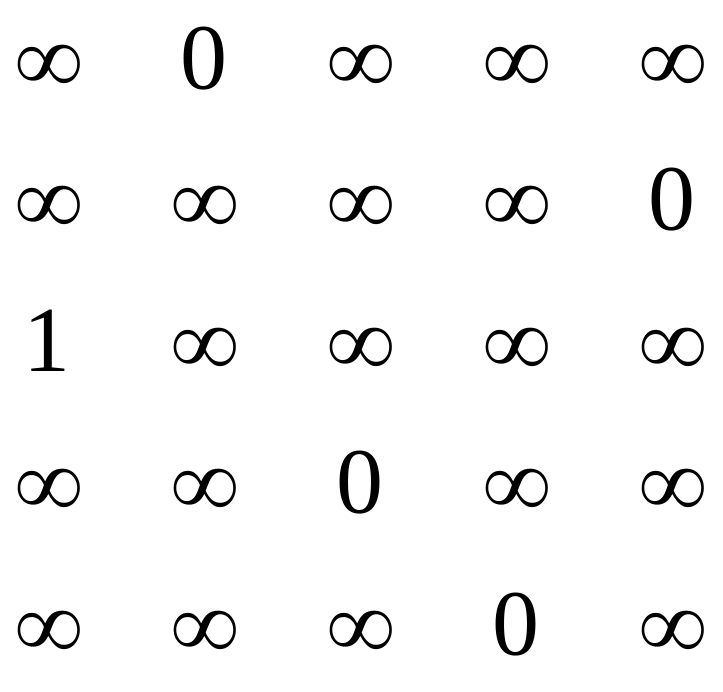

C₁₂,, C₂₅, C₅₄,,C₄₃,, C₃₁ из первого во второй

25 54 43 31 город.

С=1+3+3+1+2=10

Принимаем С за минимум, возвращаемся на 1 шаг назад (в L₄) и вычисляем матрицу R₅ (2 тур).

Ветви не имеет смысла исследовать, если нижняя граница для всех туров в данной передаче превышает стоимость наилучшего тура (минимума) в данный момент.

Матрицу R получают из исходной заменой базового элемента на , после чего повторяют процедуру поиска так же, как и для левой матрицы L, выбирая новый базовый элемент.

R₁:C₁₂=; S ; (C₁₂,, C₂₁, C₃₄,,C₃₅,, C₄₃,,C₅₃, )

C₂₁2

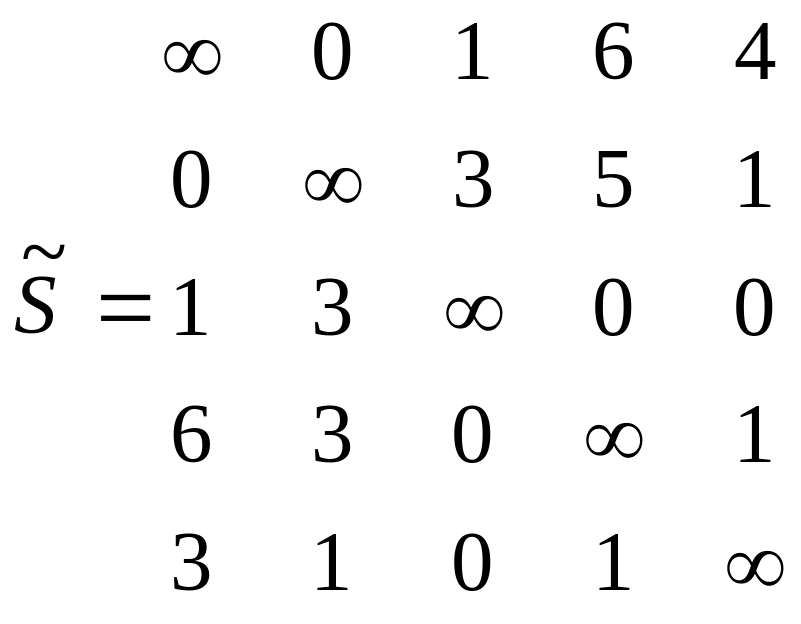
Заменяем на 

Заменяем на 0

Вывод: Проверка стоимости туров нижними границами Н_i позволяет исключать из рассмотрения большое число ветвей графа, для которых было выявлено, что Н_i>min.

Алгоритм ветвей и границ должен оптимизировать точное решение.

5.7 -отсечения.

Данный метод используется в игровых задачах, в основном для разработки биматричных игр.

Первый игрок ставит цель максимизировать свой выигрыш на каждом ходе, а второй – минимизировать свой проигрыш. Дерево решений будет строиться на основе двух стратегий: максимума (max) и минимума (min).

Пример 1:

Игра «Крестики-нолики».

Для нее можно построить полное дерево решений, однако можно не рассматривать множество «плохих» решений и отсекать «плохие» ветви.

Для определения стратегии и значений узлов дерева в этой игре используются следующие варианты:

+1 выигрыш первый игрок.

-1 выигрыш второй игрок.

0 ничья.

Листьями являются полные решения, а узлами – промежуточные состояния.

Зная значение узла, в соответствии с выбранной стратегией либо рассматривают всех потомков этого узла, либо отсекают.

Стратегии max соответствует N-четное, а стратегии min – N-нечетное, где N – порядок узлов дерева.

На первом уровне имеется 9 вариантов возможных комбинаций (поскольку все клетки игрового поля пусты), на втором уровне – 8 возможных комбинаций и т. д. Всего получается 9!=362880 листьев. Из этого числа возможных решений множество листьев дублируют друг друга.

Сложность алгоритма полного перебора O(N!).

Общее правило отсечения узлов связано с понятиями конечных и ориентировочных значений узлов. Конечное значение – это выигрыш в данной ситуации. Ориентировочное значение – это верхний предел значений узлов, находящийся в режиме min (-значения), или это нижний предел значений узлов в режиме max (-значения).

-значения характеризуют стратегию наихудшей обороны, -значения характеризуют стратегию наихудшей атаки.

Правила определения конечных и ориентировочных значений:

1. Если уже рассмотрены или отсечены все потомки некоторого узла N, то – сделать ориентировочное значение этого узла конечным значением.

2. Если ориентировочное значение узла N в режиме max равно V1, а значение одного из его потомков равно V2, то – установить ориентировочное значение узла N как функцию max(V1, V2). Если узел N в режиме min имеет значение Р1, а его потомок – значение Р2, то – установить ориентировочное значение узла N как функцию min(P1, P2).

3. Если некоторый узел P в режиме min является потомком узла Q в режиме max и ориентировочные значения их равны V1 и V2 соответственно, причем V1>V2, то можно отсечь всех нерассмотренных потомков узла Р.

Можно отсечь нерассмотренных потомков узла Q в режиме max со значением V1, предка узла Р в режиме min, имеющего ориентировочное значение V3, если выполняется условие V3<V1.

Пример 2:

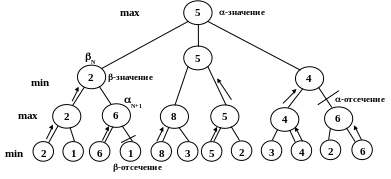 _N < _N+1

Если существует потомок узла N с -значением в режиме min, расположенный на два уровня ниже, имеющий большее значение, чем значение узла N, то можно отсечь соответствующую ветвь потомков узла N (-отсечение).

Если существует потомок для узла N с -значением в режиме max, расположенный на два уровня ниже и _N > _N+1, т. е. его значение может только уменьшить значение предка, то эту ветвь можно отсечь (-отсечение).

Преимущество данного метода перед методом перебора всех вариантов заключается в отсечении большого числа вариантов. Однако на их число влияет порядок узлов дерева, которое определяет время появления - и -отсечений. Чем раньше появляются отсечения в дереве, тем быстрее алгоритм.