
3.Аналитическая геометрия
а)-ориентация базиса
Пn n=0, 1, 2, 3
П0 – точка
П1 – прямая
П2 – плоскость
П3 – пространство
Vn – множество векторов на Пn
Vn – векторное пространство
(Пn,Vn) – аффинное пространство
dimVn=n
V1 – прямая линия
Говорят,
что 2 базиса на прямой (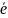 и
и
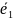 )
имеют одинаковую ориентацию, если
коэффициент пропорциональности (
)
имеют одинаковую ориентацию, если
коэффициент пропорциональности ( )
между ними больше нуля, в противном
случае они имеют противоположную
ориентацию.
)
между ними больше нуля, в противном
случае они имеют противоположную
ориентацию.
Вращение по кротчайшему пути против часовой стрелки базис называется положительным или правым, по часовой стрелке базис называется левым.
Вращение по кротчайшему пути против часовой стрелки базис называется положительным или правым, по часовой стрелке базис называется левым.
Упорядоченная тройка некомпланарных векторов называется правой, если ее векторы расположены в том же порядке что и 3 пальца правой руки.
б)-декартовые координаты
в)-аффинные системы координат
Аффинная система координат (АСК) в Пn называется пара, состоящая из точки О и базиса (О, ) векторного пространства Vn.
Любой вектор в аффинном пространстве называется радиус-вектором (аффинной прямой).
Векторное или аффинное пространство, в котором введено скалярное произведение, является Евклидовым пространством.
г)-координаты точки
д)-прямоугольная Декарта
е)-проектирование: алгебраические,геометрические
Пусть даны две непараллельные прямые на плоскости, тогда можно спроектировать вектор на прямую вдоль другой прямой
AB = AxBx + AyBy a = ax + ay (1) axox, ayoy ax, ay – геом. проекции.
Алгебраическая проекция на ось – координата геом. проекции в базисе этой прямой. пр┴e a = |a| cos(a۸e).
Разложение (1) вектора а на составляющие (геом. проекции) единственно.
Док-во: a = bx + by (1) a = (ax – bx) + (ay – by) => ax = bx ay = by
a = aπ + al(2) Разложение (2)
Прlπ a = aπ Прπl a = al
Алгебраическое проектирование – это проектирование на числовую ось. Каждый вектор приобретает координату – число. Алг. проекция вектора на координатную ось –def координата геом. проекции этого вектора на ту же ось (в той системе корд., которая на этой оси задана).
ж)-частный случай проектирования(ортогональность)
Векторы ортогональны, если их скалярное произведение=0.
з)-направляющие углы
i, j, k – ОНБ (ортонормированный базис) ā = a1i + a2j + a3k a≠Ō В ОНБ i, j, k {ā*i = a1; ā*j = a2; ā*k = a3}(2) = {|ā|cos(a۸i) = a1; |ā|cos(a۸j) = a2; |ā|cos(a۸k) = a3} = {a1 = |ā|cosα; a2 = |ā|cosβ; a3 = |ā|cosγ}(3) α = ā۸i, β = ā۸j, γ = ā۸k. Косинусы углов α, β и γ назыв. направляющими косинусами вектора ā.
и)-косинусы векторов
к)-векторное произведение
Векторным произведением a на b называется вектор c, что:
| |=| || |sin( ^ )
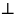 ,
,
, , – правая
Замечание. Определение годится для неколлинеарных векторов a и b.
л)-свойства векторного произведения
1. [ , ] = 0 || (векторы коллинеарны, когда хотя бы один из множителей 0)
2.
[
,
]
= -[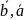 ]
]
3.
[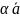 ,
]
=
[
,
]
,
]
=
[
,
]
4.
[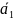 +
+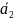 ,
]
= [
,
]
+ [
,
]
,
]
= [
,
]
+ [
,
]
м)-смешанное произведение
Смешанное
произведение векторов
,
,
в указанном порядке называется число:
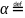 ([
,
],
).
([
,
],
).
Векторное пространство называется ориентированным, если в этом пространстве осуществлен выбор одного из двух классов одинаковых ориентированных базисов.
н)-свойства смешанного произведения(2 леммы)
Свойства:
При циклической перестановке векторов базиса мы получаем базис той же ориентации что и исходной
Если 2 вектора базиса поменять местами, то получится новый базис противоположной ориентации.
Леммы:
Упорядоченная тройка некомпланарных , , векторов является правой тогда и только тогда, когда проекция на
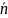 >0.
>0.
n - ортогональный и ; , , - прав.
Если любой фиксированный вектор
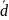 любому вектору
любому вектору
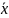 =>
=0
=>
=0
Коментарий: При этом 2 и 3 условия бессмысленны, если хотя бы один из данных векторов является нулем.
