
0.Историческая справка
Основным предметом, о котором пойдет речь в рамках, условно говоря, излагаемого курса аналитической геометрии, является евклидова планиметрия и стереометрия. Строгое аксиоматическое изложение геометрии состоялось около 300 г. до н.э. Оно принадлежит Евклиду и содержится в его всемирно знаменитом труде «Начала», состоящем из 13 книг. Этот труд до сих пор остается одной из величайших, сверкающих и труднодостижимых вершин человеческого знания, несмотря на 2300 лет следующего за Евклидом периода непрерывного развития как человечества в целом, так и геометрии, в частности. Строгое аксиоматическое построение геометрии обычно не включается в аналитическую геометрию. Не содержится оно и в данной работе. Аксиоматическое изложение – отдельная геометрическая дисциплина – основания геометрии. Ниже всюду будет использоваться в полном объеме школьная евклидова геометрия. Метод изучения – аналитический, или координатный – открыт Рене Декартом(Картезием) в 1637 г.
1.Слау. Определители. Матрицы.
СЛАУ- системы линейных алгебраических уравнений
а) -общие понятия
Система равенства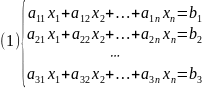 в которой
в которой
 ,
,
 носит
носит
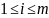 ;
;
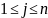 название СЛАУ
содержащей n
неизвестных
название СЛАУ
содержащей n
неизвестных
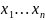 и состоящих из
и состоящих из
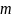 уравнений, при этом
уравнений, при этом
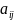 –
коэффициент находящийся в i-строке
и j-столбце,
bi
– свободный член.
–
коэффициент находящийся в i-строке
и j-столбце,
bi
– свободный член.
б) -общие определения решений
Решение СЛАУ
(частного отдельно взятого) называется
всякий упорядоченный набор чисел в
общем случае вещественных состоящих
из n
вещ-х чисел α=(
α1,
α2,.....,
αn)
αj
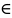 R
при подстановке которых в уравнение
системы вместо соответствующих
неизвестных, каждое уравнение СЛАУ
становится верным числовым
неравенством(тождеством).
R
при подстановке которых в уравнение
системы вместо соответствующих
неизвестных, каждое уравнение СЛАУ
становится верным числовым
неравенством(тождеством).
в) -системы: совместные/несовместные
Система называется совместной, если множество ее решений не пусто (если хотя бы допускает одно решение) и несовместной в противном случае.
Совместная система называется определенной, если у нее есть одно решение и неопределенной в противном случае.
г)-коэффициенты. Неизвестные
a11x1 + a12x2 + ……+ a1nxn = b1} aij, bi – коэффициенты (действ. числа)
a21x1 + a22x2 + …... + a2nxn = b2} (1) aij – коэф. при неизвестных xj(R или С) 1≤i≤m, 1≤j≤n.
... ... ... …
am1x1 + am2x2 + … + amnxn = bm} m – число ур-ний, n – число неизвестных.
д)-расширенные матрицы
Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
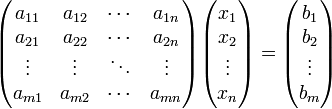
Или Ax=B
е)-формы записи СЛАУ
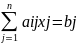
СЛАУ(1)
Расширенная матрица
∑nj=1 aij xj= bi (1≤ i ≤m)
A ∙ X=B
ж)-элементарные преобразования СЛАУ
1) перемена местами уравнений
2) умножение на любое число не равное 0
3) прибавление какого-либо уравнения, к другому уравнению предварительно умноженное на любое число.
4) добавление (отбрасывание) уравнения, тождества = 0
з)-элементарные преобразования СЛАУ (теорема).
В результате элементарных преобразований из СЛАУ(1) приводится к новой СЛАУ(2) равносильной исходной.
и)-эквивалентные матрицы
Системы СЛАУ 1 и 2 с одним и тем же числом неизвестных n называются равносильными (эквивалентными), если их множество решений совпадают.
к)-метод Гаусса
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn
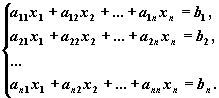
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
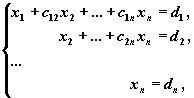
решение которой находят по рекуррентным формулам:
Шаг. Прямой ход метода Гаусса: приведение расширенной матрицы системы
 к
ступенчатому виду
к
ступенчатому виду
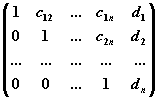 с
помощью элементарных
операций над строками
матрицы.
с
помощью элементарных
операций над строками
матрицы.
Шаг.
Обратный ход
метода Гаусса: преобразование полученной
ступенчатой матрицы к матрице, в первых
n
столбцах которой содержится единичная
матрица
 ,
последний, (n+1)-й,
столбец этой матрицы содержит решение
системы.
,
последний, (n+1)-й,
столбец этой матрицы содержит решение
системы.
л)-теорема Крамера (с доказательством)
Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1 , x2 , ..., xn, определяемое формулами Крамера
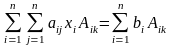
Видно, что
 k
это определитель, получающийся из
заменой столбца с номером k
столбцом свободных членов.
k
это определитель, получающийся из
заменой столбца с номером k
столбцом свободных членов.
Xk = k / , k=1,2, ..., n. – Формула Крамера
Если
определитель
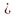 0
и система совместна, то она имеет
единственное решение, находящиеся по
формуле Крамера.
0
и система совместна, то она имеет
единственное решение, находящиеся по
формуле Крамера.
м)-алгоритмы
Алгоритм основан на след. фактах и понятиях:
1) на понятии элементарного преобразования СЛАУ
2) на теореме о том, что всякое элементарное преобразование переводит исходное СЛАУ к новой СЛАУ эквивалентной (равносильной) системе.
Алгоритм:
Не нарушая общности будем считать, что:
Неизвестные x1 входит в 1-ре ур. сис. (по существу), т.е с ненулевым коэфицентом (а11 ǂ0). Счиатя это предположение выполненным: исключаем неизвестное x1 из всех уравнений системы, кроме 1-ого.
Неизвестное x1 из 2-ого уравнения:
Первое уравнение
умножаем
 и
результат прибавляем по 2-ому =˃
и
результат прибавляем по 2-ому =˃
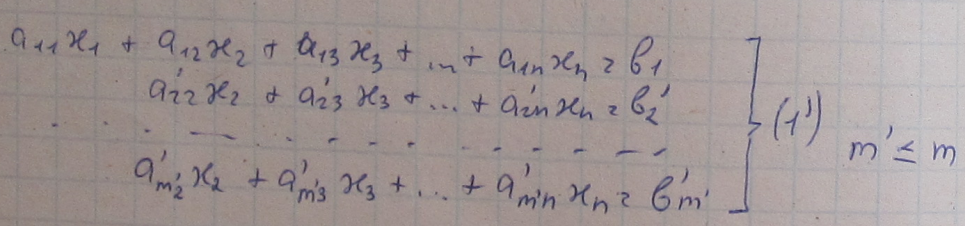
Пояснение: неизвестное х1 исключено из всех, кроме 1-ого уравнения системы. При этом число уравнений может уменьшится или остаться неизменным.
г) Повторение 1-ого шага, но в системе:
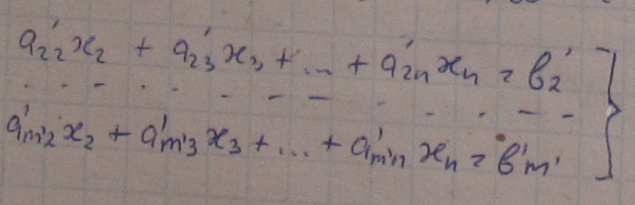
Оказывается при этом, в результате применения метода Гауса, возможны 3 исхода, к которым приводит этот метод:
1) заключается в том, что на каком-то шаге получается уравнение вида 0=b (≠0) - нет решений.
2) Матрица системы приводится к треугольному виду (к верхтреугольному) к такому, что на главной диагонали нет нулей. В этом случае получается единственное решение.
3)матрица системы приводится к виду трапеции

В этом случае системы имеет бесконечное число решений (множество решений)
н)-определители малого порядка
Существует очень важная характеристика квадратичной матрицы - определитель(детерминант)
Определитель квадратичной матрицы порядка n - это число, которое по некоторому правилу ставится в соответствие каждой квадратной матрице (функция матрицы)
Определитель малых порядков т.е порядка n, для n=1,2,3
1) n=1 - определитель матрицы первого порядка.
2) Второго порядка:
А=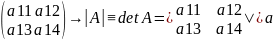 11
11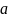 22-
12
21
22-
12
21
о)-Виды матриц
Квадратная - n-го порядка называется матрица размера n×n.
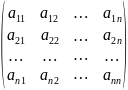
Прямоугольная- матрица размера m x n.
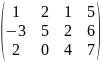
Диагональная (Квадратно-диагональная)- квадратная матрица, у которой все элементы вне главной диагонали равны нулю.
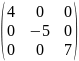
Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.
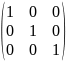
Нулевой называется матрица, все элементы которой равны нулю.

Скалярная - a ∙ En
п)-действия над матрицами
Сложение матриц. (Можно складывать матрицы одного и того же размера. Для сложения нужно сложить элементы стоящие на одних и тех же местах.)
Умножение матриц на число. (Можно умножить на любое число. Для этого нужно умножить каждый элемент на число.)
Умножение матрицы на матрицу(можно складывать любые две матрицы одинаковых размеров)
нужно чтобы совпадало число столбцов1-й матрицы и строк 2-й. Произведением матрицы Аm×n на матрицу Вn×p, называется матрица Сm×p такая, что сik = ai1 × b1k + ai2 × b2k + ... + ain × bnk, т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В.
р)-свойства линейных операций
Замечание A, B, C… Є Mmxn – множество матриц размером mxn.
P=R(C), где P-числовое поле.
(A+B)+C=A+(B+C) –ассоциативность
Существует O Є M | A+O=O+A=A – существование нейтрального элемента
Для всякого A Є M существует –А | A+(-A)=(-A)+A=O – существование симметричного(противоположного) элемента
A+B=B+A – коммутативность
Замечание 2.
Если на множестве каких-либо объектов введено действие, обладающее какими-либо свойствами (например 1, 2, 3), то это множество называется группой, а операция – умножением. Если все 4 – абелевая или коммутативная группа, умножение называется тогда сложением.
a(A+B)=aA+aB - дистрибутивность
(a+b)A=aA+bA - дистрибутивность
(ab)A=a(bA)
1 ∙ A=A
с)-обратные матрицы. алгоритм нахождения
Матрица B
называется
обратной матрицей для
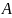 ,
если
,
если
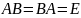 ,
где
,
где
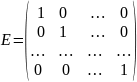 – единичная. (
– единичная. ( )
)
Обратные матрицы (алгоритм)
Если дана произвольная матрица А
Составить Ат (транспортировочная матрица)
Найти алгебраическое дополнение к Ат
Составить А* (присоединенная матрица, союзная матрица для А)
Получить А-1 по формуле А-1=|1A| ∙ А* (|A| - детерминант матрицы А
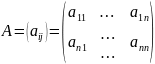

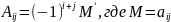
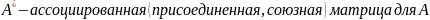
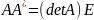
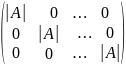 =
=
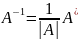
n=1
A= (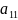 =a)
=a)
 a
a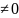
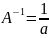
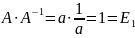
h=2
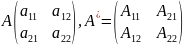
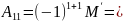

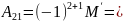
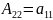

т)-миноры
Минор матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк и столбцов.
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
у)-элементы комбинаторики
Произвольное расположение m символов, выбранных из n элементов называется размещение (Amn = n(n-1)*…*[n-(m-1)]). Всякое размещение из n по n приводит к понятию перестановки из n-символов (Pn = Ann = n(n-1)*…*2*1=1*2*3*…*(n-1)*n=n!) Если из множества n-символов выбирать подмножество из m-символов получается сочетание (Cmn = Amn/Pm = (Amn*Pnn-m)/(Pm*Pn-m) = Pn/(Pn*Pn-m)).
ф)-определители n-го порядка
Определитель порядка n называется число равное алгебраической сумме n! Слагаемых каждый из которых предполагает из произведение n членов определителя взятых по одному и только по одному из каждой его строки и каждого столбца. При этом слагаемое или произведение берется со знаком «+» если подстановка составлена из номеров строк и номеров столбцов входящих в данное произведение четное, со знаком «-» - нечетное.
ц)-перестановка из n-символов
Перестановкой из n-символов называется расположение этих символов в определённом порядке.
Говорят, что числа …i…..j…..образуют инверсию, если большее стоит левее меньшего (i>j).
Транспозиция – перемена местами 2х символов.
После транспозиции чётность меняется на нечётность и наоборот
Все n! перестановок из n символов можно расположить в таком порядке, что каждая последующая будет получаться из предыдущей 1 транспозицией.
Биективное соответствие множества, состоящего из n-символов, называется подстановкой.
Любая подстановка в записи может быть представлена 2мя перестановками, записанными друг под другом.
Каждая подстановка может быть записана n! способами.
ч)-четность\нечетность
Четностью перестановки называют общее число инверсий.
Если число инверсий четное, то перестановка четная, если это число нечетное, то перестановка нечетная.
щ)-общее определение детерминанта.
Определителем (детерминантом) порядка n (квадратная матрица порядка n) называется число, равное алгебраической сумме n! слагаемых, каждое из которых представляет из себя произведения n-членов определителя, взятой по 1 и только по 1, взятое из каждой его строки и каждого столбца. При этом слагаемое берётся со знаком +, если подстановка, составленная из номеров строк и столбцов, входящих в данное произведение членов, чётная и со знаком -, если подстановка нечётная.
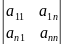 =
=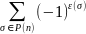
ы)-свойства определителей
1- Определитель не меняется при транспозиции.
Замечание: Любое свойство для строк справедливо и для столбцов
2- Определитель содержащий строку из одних нулей, сам равен нулю
3- Если какую-либо строку определителя умножить на некоторое число, то и сам определитель умножается на это число.
4- Если поменять местами 2-ую строку, то определитель изменит знак на противоположный.
5- Если в определителе изменяются 2-е одинаковые строки, то он равен нулю.
6- Если в определителе имеются пропорциональные строки, то он равен нулю.
7- Если в определителе какая-либо строка представляет из себя сумму некоторых 2х пропорциональных матриц строк, тогда определитель равен сумме 2х определителей, у каждого из которых все строки кроме упомянутой те же самые, что и в исходном определителе.
8- Если к какой-либо строке определит любую другую его строку, предварительно умноженное на любое число, то определитель не изменится.
