
2.Геометрические векторы:
а)-свойства
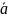 +
+
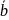 +
+
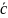 =
+ (
+
)
- Ассоциативность
сложения
=
+ (
+
)
- Ассоциативность
сложения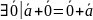 =
=
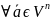 (n=0,1,2,3)
(n=0,1,2,3)
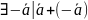 =
=
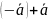 =0
=0
1-4 это абилева группа или коммутативная
+ = + - Коммутативность сложения
 - Дистрибутивность
умножения на число относительно сложения
векторов
- Дистрибутивность
умножения на число относительно сложения
векторов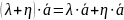 - Дистрибутивность
умножения на число относительно сложения
чисел
- Дистрибутивность
умножения на число относительно сложения
чисел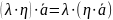 -
Ассоциативность
умножения на число
-
Ассоциативность
умножения на число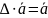
1-8 имеют место для
любых
,
,

б)-линейные комбинации
Линейная комбинация
– вектор
равен сумме произведений
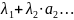
Вектор b = ∑mi=1λiai = λ1a1 + … + λmam назыв. линейной комбинацией векторов системы Am, а числа λ1, …, λm назыв. коэффиц. данной линейной комбинации.
Линейные комбинации называется тривиальной, если все ее коэффициенты = 0
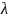 1 =
2
= ... +
m
= 0
1 =
2
= ... +
m
= 0
в)-зависимость(независимость)
Системы векторов Ам называется линейно зависимой, если сущ-ет нетривиальная линейная комбинация ее векторов = 0. В противном случае система Ам называется линейно-независимой.
Система Ам называется линейно независимой, если равенство 0 ее линейной комбинации возможно, только в тривиальном варианте.
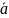
 ,
b
= -
,
(-
)
= 0 (комбинация не тривиальна, но она
равна 0)
,
b
= -
,
(-
)
= 0 (комбинация не тривиальна, но она
равна 0)
Система Аm линейно зависима тогда и только тогда, когда один из векторов этой системы линейно выражается через остальные векторы этой же системы.
Система Am линейно независима тогда и только тогда, когда всякий вектор линейно выражающийся через нее единственен.
г)-критерии линейной независимости(док-во)
1) необходимость лин. зав. Пусть Am – лин-зав, т. е. лин. нетрив. комб. ∑mi=1λiai=Ō λioaio + ∑mi=1(i≠io)λiai=Ō=>aio=∑mi=1(i≠io)μiai μi=–λi/λio 2) достаточность. Пусть вектор aioAm ∑mi=1λiai–1*aio= Ō Критерий лин. незав.: система векторов Am лин-незав. який вектор, линейно через нее выражающийся выражается через нее единственным способом. Док-во: 1) необходимость. Пусть Am лин-незав. a=∑mi=1λiai Пусть a=∑mi=1μiai a=∑mi=1(λi – μi)ai (λi – μi = γi) ∑mi=1 γiai = Ō => γi=0, т.е. λi = μi 2) достаточность. Пусть любой вектор, линейно-выражающийся через Am, т.е. такой, что a=∑mi=1λiai единств. образом. Ō=∑mi=1ηiai при ηi = 0 ∑mi=1λiai=Ō => λi = μi =0
д)-базисы
Система векторов AmV называется полной, если всякий aV линейно выражается через векторы этой системы a=∑mi=1λiai.
Упорядоченная система векторов An=(a1, …,an) называется базисом векторного пространства V, если An – лин. незав. и полная.
1) Тривиальное пространство, сост. из Ō не имеет базиса.
2) Базис векторов на прямой – это любая система, сост. из одного ненулевого вектора.
3) Любая пара неколлинеарных векторов на плоскости образует базис.
4) Любая тройка некомпланарных векторов образует базис в пространстве.
Теорема. Если сущ. конечный базис An, n≠0 в векторном пространстве V, то любые два базиса состоят из одного и того же числа векторов.
е)-размерности
Размерностью векторного пространства называется число векторов его базиса. (это опр. и теория формируются при условии. что выполняется аксиома размерности).
