
- •3. Определение определителя 3-го порядка как обобщение записи определителя 2-го порядка и геометрической схемы (правила) формирования членов определителя, то есть его вычисления.
- •8,9. Миноры и алгебраические дополнения
- •18.Ранг матрицы: определение и способы его вычисления.
- •19.Определение системы линейных уравнений. Классификация систем линейных уравнений
- •20.Матричная форма записи систем линейных уравнений
- •21.Схема применения правила Крамера при решении системы линейных уравнений
- •22.Схема решения системы линейных уравнений методом Гауса
- •23.Теорема Кронекера-Капелли: с доказательством и иллюстрацией применения.
- •24.Схема исследования и решения системы линейных уравнений в общем случае.
- •31. Сложение и умножение линейных преобразований.
- •33. Вычисление собственных векторов и значений методом прямых итераций
31. Сложение и умножение линейных преобразований.
Линейные преобразования можно складывать и умножать.
Преобразование ![]() называется линейным,
если выполнены следующие условия:
называется линейным,
если выполнены следующие условия:
1![]()
![]() ,
,
2
![]() .
.
Определение
9.2 Произведением
линейных преобразований
и ![]() называется
преобразование
называется
преобразование ![]() ,
состоящее в последовательном выполнении
сначала преобразования
,
а затем преобразования
.
,
состоящее в последовательном выполнении
сначала преобразования
,
а затем преобразования
.
Другими
словами: ![]() означает,
что для любого
означает,
что для любого ![]()
![]() .
.
Произведение линейных преобразований есть линейное преобразование, т.е. удовлетворяет условиям 1 и 2 определения 1. Действительно,
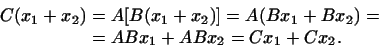
Первое равенство написано на основании определения произведения, второе на основании свойства 1 для , третье в силу того же свойства для и, наконец, четвертое опять-таки в силу определения произведения.
Аналогично
показывается, что ![]() .
.
Если ![]() --
единичное преобразование, а
--
произвольное, то легко проверить, что
--
единичное преобразование, а
--
произвольное, то легко проверить, что
![]()
Как обычно, определяем степени преобразования :
![]() и т.д.
и т.д.![]()
Как
и для чисел, полагаем, по определению, ![]() .
Очевидно, что
.
Очевидно, что
![]()
32.
Собственные
векторы и собственные значения линейного
оператора
Ненулевой
вектор ![]() называется
собственным вектором линейного
оператора
называется
собственным вектором линейного
оператора ![]() ,
если
,
если ![]() (
(![]() для
комплексного
),
такое, что
для
комплексного
),
такое, что ![]() Число
Число ![]() называется
собственным числом (собственным
значением) оператора f,
соответствующим этому собственному
вектору.
называется
собственным числом (собственным
значением) оператора f,
соответствующим этому собственному
вектору.
Если
в некотором базисе оператор f имеет
матрицу А и
в том же базисе вектор
имеет
координатный столбец X,
то ![]() или
или ![]()
Собственные
числа
линейного
оператора
-
корни характеристического уравнения ![]() ,
где
,
где ![]() -
матрица оператора f,
-
матрица оператора f, ![]() -
символ Кронекера.
-
символ Кронекера.
Для
каждого собственного значения ![]() соответствующие
собственные векторы могут быть найдены
из матричного уравнения
соответствующие
собственные векторы могут быть найдены
из матричного уравнения ![]() или
соответствующей ему системы линейных
уравнений
или
соответствующей ему системы линейных
уравнений
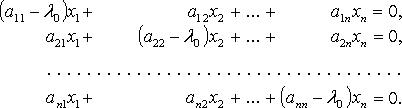
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид

где ![]() -
соответствующие собственные значения.
-
соответствующие собственные значения.
33. Вычисление собственных векторов и значений методом прямых итераций
Самым
простым способом численного нахождения
собственных значений и собственных
векторов является метод прямых итераций.
Он заключается в построении
последовательности векторов ![]() ,
,![]() ,
, ![]() ,
,![]() и
т. д., то есть в многократном домножении
случайного ненулевого начального
вектора v0 на
матрицу M. Можно доказать, что если
вектор
имеет
ненулевые проекции на все собственные
вектора M (случайное взятие
координат
гарантирует
это с почти единичной вероятностью), то
такой итеративный процесс сойдётся к
собственному вектору
и
т. д., то есть в многократном домножении
случайного ненулевого начального
вектора v0 на
матрицу M. Можно доказать, что если
вектор
имеет
ненулевые проекции на все собственные
вектора M (случайное взятие
координат
гарантирует
это с почти единичной вероятностью), то
такой итеративный процесс сойдётся к
собственному вектору ![]() ,
соответствующему максимальному
собственному значениюλmax.
Вычисление остальных собственных
значений возможно с помощью
вычитания проекции очередного
вектора итераций на подпространство
из уже полученных векторов.
,
соответствующему максимальному
собственному значениюλmax.
Вычисление остальных собственных
значений возможно с помощью
вычитания проекции очередного
вектора итераций на подпространство
из уже полученных векторов.
Недостаток этого метода заключается в том, что он не работает на матрицах, у которых совпадает абсолютная величина каких-то двух собственных значений. Например, таким образом невозможно найти ни одного собственного вектора дискретного косинусного преобразования: так как оно является обратным по отношению к самому себе, то повторное его применение к случайному вектору приведёт к заведомо расходящейся последовательности, состоящей из двух чередующихся векторов.
Пример 19.10 Найдите собственные числа и собственные векторы матрицы
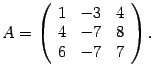
Решение. Составляем
характеристическую матрицу ![]() :
:
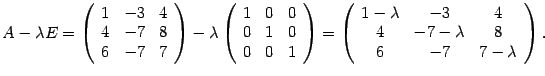
Находим характеристический многочлен
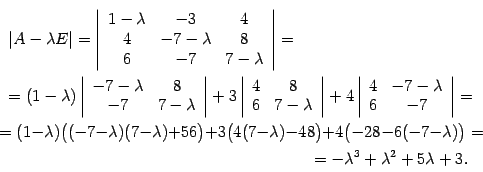
Решим характеристическое уравнение
![]()
Подбором
находим, что один корень уравнения
равен ![]() .
Есть теорема, которая говорит, что если
число
.
Есть теорема, которая говорит, что если
число ![]() является
корнем многочлена
является
корнем многочлена ![]() ,
то многочлен
делится
на разность
,
то многочлен
делится
на разность ![]() ,
то есть
,
то есть ![]() ,
где
,
где ![]() --
многочлен. В соответствии с этой теоремой
многочлен
--
многочлен. В соответствии с этой теоремой
многочлен ![]() должен
делиться на
должен
делиться на ![]() .
Выделим в характеристическом многочлене
этот множитель
.
Выделим в характеристическом многочлене
этот множитель ![]() :
:
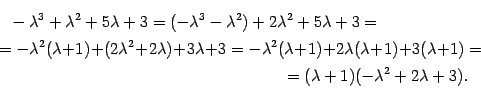
Находим
корни трехчлена ![]() .
Они равны
и
3. Таким образом,
.
Они равны
и
3. Таким образом,
![]()
![]() --
корень кратности 2 17.7 b,
--
корень кратности 2 17.7 b, ![]() --
простой корень. Итак, собственные числа
матрицы
--
простой корень. Итак, собственные числа
матрицы ![]() равны
,
.
Найдем соответствующие им собственные
векторы.
равны
,
.
Найдем соответствующие им собственные
векторы.
Пусть ![]() ,
тогда для собственного вектора
,
тогда для собственного вектора ![]() получаем
матричное уравнение
получаем
матричное уравнение
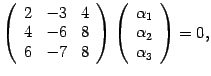
что соответствует системе уравнений
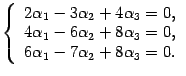
Решаем ее методом Гаусса (раздел "Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)"). Выписываем расширенную матрицу системы
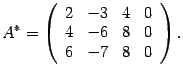
Первую
строку, умноженную на числа ![]() и
и ![]() прибавляем
соответственно ко второй и третьей
строкам
прибавляем
соответственно ко второй и третьей
строкам
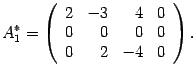
Меняем местами вторую и третью строки
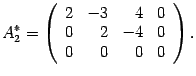
Возвращаемся к системе уравнений
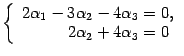
Базисный
минор матрицы ![]() находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальня
система содержит только одно решение.
Переменные
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальня
система содержит только одно решение.
Переменные ![]() и
и ![]() оставляем
в левой части, а переменное
оставляем
в левой части, а переменное ![]() переносим
в правую часть
переносим
в правую часть
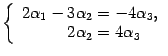
Полагаем ![]() ,
находим
,
находим ![]() ,
, ![]() .
Итак, собственному числу
соответствует
собственный вектор
.
Итак, собственному числу
соответствует
собственный вектор 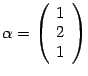 .
.
Пусть ![]() ,
тогда для собственного вектора
,
тогда для собственного вектора ![]() получаем
матричное уравнение
получаем
матричное уравнение
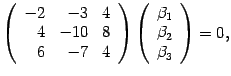
что соответствует системе уравнений
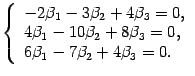
Решаем ее методом Гаусса. Выписываем расширенную матрицу

Первую строку умножаем на числа 2 и 3 и прибавляем соответственно ко второй и третьей строкам
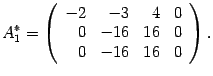
Вторую строку умножаем на и прибавляем к третьей
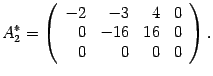
Возвращаемся к системе уравнений
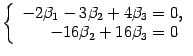
Базисный
минор матрицы
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальная
система содержит только одно решение.
Переменные ![]() и
и ![]() оставляем
в левой части, а переменное
оставляем
в левой части, а переменное ![]() переносим
в правую часть
переносим
в правую часть
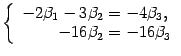
Полагаем ![]() ,
находим
,
находим ![]() ,
, ![]() .
Итак, собственному числу
соответствует
собственный вектор
.
Итак, собственному числу
соответствует
собственный вектор 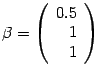 .
Чтобы избавиться от дроби, умножим
собственный вектор на 2, получим
собственный вектор с тем же самым
собственным числом. В итоге собственному
числу
соответствует
собственный вектор
.
Чтобы избавиться от дроби, умножим
собственный вектор на 2, получим
собственный вектор с тем же самым
собственным числом. В итоге собственному
числу
соответствует
собственный вектор 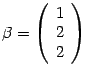 .
.
Ответ: Собственные числа: , , соответствующие собственные векторы: , .
