
- •3. Определение определителя 3-го порядка как обобщение записи определителя 2-го порядка и геометрической схемы (правила) формирования членов определителя, то есть его вычисления.
- •8,9. Миноры и алгебраические дополнения
- •18.Ранг матрицы: определение и способы его вычисления.
- •19.Определение системы линейных уравнений. Классификация систем линейных уравнений
- •20.Матричная форма записи систем линейных уравнений
- •21.Схема применения правила Крамера при решении системы линейных уравнений
- •22.Схема решения системы линейных уравнений методом Гауса
- •23.Теорема Кронекера-Капелли: с доказательством и иллюстрацией применения.
- •24.Схема исследования и решения системы линейных уравнений в общем случае.
- •31. Сложение и умножение линейных преобразований.
- •33. Вычисление собственных векторов и значений методом прямых итераций
24.Схема исследования и решения системы линейных уравнений в общем случае.
Пусть заданная система m линейных уравнений с n неизвестными общего вида
a11x1+a12x2+…+a1nxn=b1,
a21x1+a22x2+…+a2nxn=b2,
…………………………………….
Am1x1+am2x2+…+amnxn=bm, (2)
или, в матричной форме,
AX=B, (3)
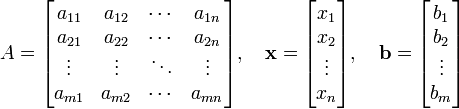
Если В=0, то система называется однородной, в противном случае она называется неоднородной.
Решением системы(2) называется всякий n-компонентный вектор-столбец Х, обращающий матричное уравнение (3) в равенство (соответствующий решению Х арифметический вектор х принадлежит R n также будем считать решением системы (2) )
Система называется совместной, если у нее существует, по крайней мере, одно решение, в противно случае она называется несовместной.
Две системы называются эквивалентными, если множества их решений совпадают.
25. Однородные системы линейных уравнений
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:
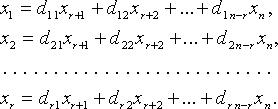
Тогда n - r линейно независимыми вектор-решениями будут:
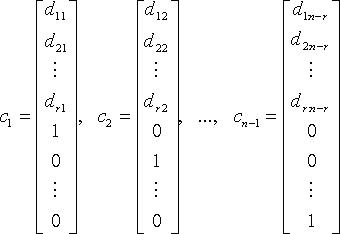
а любое
другое решение является их линейной
комбинацией. Вектор-решения ![]() образуют
нормированную фундаментальную систему.
образуют
нормированную фундаментальную систему.
В
линейном пространстве ![]() множество
решений однородной системы линейных
уравнений образует подпространство
размерности n
- r;
-
базис этого подпространства.
множество
решений однородной системы линейных
уравнений образует подпространство
размерности n
- r;
-
базис этого подпространства.
26. Общее решение неоднородной системы линейных уравнений равно сумме общего решения приведенной однородной системы и любого частного решения неоднородной системы.
Поскольку общее решение линейной системы, записанной в каноническом виде, определяется формулами:
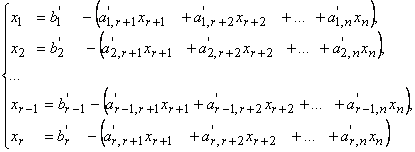
то общее решение неоднородной системы можно записать в векторной форме в виде:
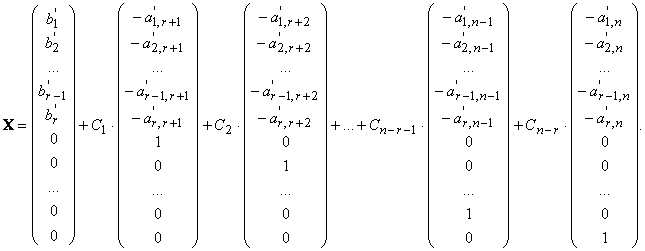
Здесь С1, С2, ..., Сn−r−1, Сn−r — произвольные константы, r — ранг матрицы системы.
Любая однородная система линейных алгебраических уравнений, ранг матрицы которой равен r, с помощью элементарных преобразований может быть приведена к каноническому виду:
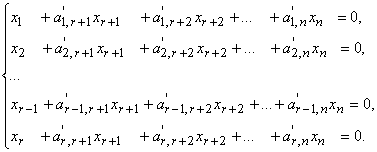
Общее решение однородной линейной системы, записанной в каноническом виде, очевидно, определяется формулами:
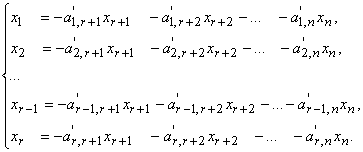
Свободные переменные xr+1 , xr+2 , ..., xm−1, xm могут принимать произвольные значения.
Вычисленные по этим формулам n − r линейно независимых решений образуют фундаментальную систему решений:

Тогда общее решение системы можно записать в вектороной форме в виде:
![]()
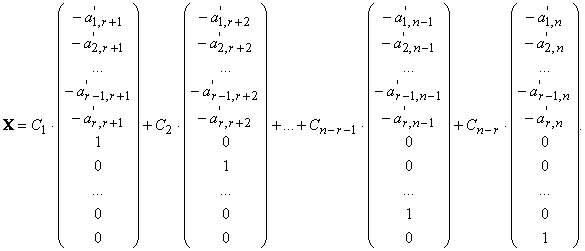
Здесь С1, С2, ..., Сn−r−1, Сn−r — произвольные константы.
27.
Определение
линейного пространства
Пусть V -
непустое множество (его элементы будем
называть векторами и обозначать ![]() ...),
в котором установлены правила:
...),
в котором установлены правила:
1)
любым двум элементам ![]() соответствует
третий элемент
соответствует
третий элемент ![]() называемый
суммой элементов
называемый
суммой элементов ![]() (внутренняя
операция);
(внутренняя
операция);
2)
каждому ![]() и
каждому
и
каждому ![]() отвечает
определенный элемент
отвечает
определенный элемент ![]() (внешняя
операция).
(внешняя
операция).
Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:
I. ![]()
II. ![]()
III. ![]() (нулевой
элемент, такой, что
(нулевой
элемент, такой, что ![]() ).
).
IV. ![]() (элемент,
противоположный элементу
(элемент,
противоположный элементу ![]() ),
такой, что
),
такой, что ![]()
V. ![]()
VI. ![]()
VII. ![]()
VIII. ![]() Аналогично
определяется комплексное линейное
пространство (вместо R рассматривается C).
Аналогично
определяется комплексное линейное
пространство (вместо R рассматривается C).
Линейная зависимость и независимость векторов
Система ![]() линейно
зависима,
линейно
зависима,
![]()
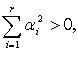 что
что 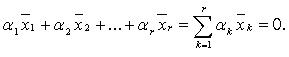
Критерий линейной зависимости векторов
Для
того чтобы векторы ![]() (r
> 1)
были линейно зависимы, необходимо и
достаточно, чтобы хотя бы один из этих
векторов являлся линейной комбинацией
остальных.
(r
> 1)
были линейно зависимы, необходимо и
достаточно, чтобы хотя бы один из этих
векторов являлся линейной комбинацией
остальных.
28.
Определение.
Линейное пространство ![]() называется
называется ![]() -мерным,
если в нем существует
линейно
независимых векторов, а любые из
-мерным,
если в нем существует
линейно
независимых векторов, а любые из ![]() векторов
уже являются зависимыми. Другими словами,
размерность пространства — это
максимальное число содержащихся в нем
линейно независимых векторов.
Число
называется
размерностью пространства
и
обозначается
векторов
уже являются зависимыми. Другими словами,
размерность пространства — это
максимальное число содержащихся в нем
линейно независимых векторов.
Число
называется
размерностью пространства
и
обозначается ![]() .
.
Определение. Совокупность линейно независимых векторов -мерного пространства называется базисом.
Справедлива следующая теорема.
Базисом
векторного пространства ![]() называется
любая независимая система линейно
независимых
–векторов
этого пространства, количество которых
равно
,
т.е. выбор системы базисных векторов
векторного пространства
неоднозначен,
и может быть осуществлен большим числом
способов.
называется
любая независимая система линейно
независимых
–векторов
этого пространства, количество которых
равно
,
т.е. выбор системы базисных векторов
векторного пространства
неоднозначен,
и может быть осуществлен большим числом
способов.
29.
Теорема.
Каждый вектор ![]() линейного
пространства
можно
представить и притом единственным
способом в виде линейной комбинации
векторов базиса
линейного
пространства
можно
представить и притом единственным
способом в виде линейной комбинации
векторов базиса ![]() :
:
![]()
Это
равенство называется разложением
вектора
по
базису
,
а числа ![]() —
координатами вектора
—
координатами вектора ![]() относительно
этого базиса. В силу единственности
разложения каждый вектор однозначно
может быть определен координатами в
некотором базисе.
относительно
этого базиса. В силу единственности
разложения каждый вектор однозначно
может быть определен координатами в
некотором базисе.
Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, – противоположные по знаку координаты.
Теорема. Если – система линейно независимых векторов пространства и любой вектор линейно выражается через , то пространство является -мерным пространством , а векторы – его базисом.
Нередко приходится встречаться с заменой переменных, при которой старые переменные линейно выражаются через новые, например, при переходе от одного базиса пространства к другому. Такую замену переменных называют обычно их линейным преобразованием.
30.
Линейным
преобразованием переменных называется
выражение системы переменных ![]() через
новую систему переменных
через
новую систему переменных ![]() с
помощью линейных однородных функций:
с
помощью линейных однородных функций:

Линейное
преобразование вполне определяется
таблицей размером ![]() ,
составленной из коэффициентов при
.
Такая таблица, составленная из
элементов
,
составленной из коэффициентов при
.
Такая таблица, составленная из
элементов ![]() называется
матрицей
называется
матрицей ![]() ,
а само преобразование представляет
собой пример матричной операции.
,
а само преобразование представляет
собой пример матричной операции.
