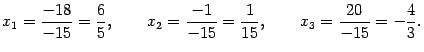18.Ранг матрицы: определение и способы его вычисления.

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Существует несколько методов нахождения ранга матрицы:

• Метод элементарных преобразований

Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

• Метод окаймляющих миноров

Пусть в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

19.Определение системы линейных уравнений. Классификация систем линейных уравнений

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида 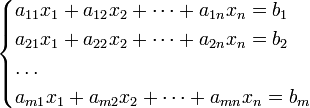(1)

(1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (_i) и неизвестного (_j), при котором стоит этот коэффициент, соответственно.

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких, что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁(1), c₂(1), …, c_n(1) и c₁(2), c₂(2), …, c_n(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:c₁(1) = c₁(2), c₂(1) = c₂(2), …, c_n(1) = c_n(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

20.Матричная форма записи систем линейных уравнений

Матричная форма записи

В матричной записи система линейных уравнений может быть записана следующим образом:

AX=B

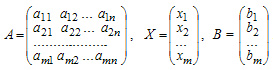
Пример 2: Записать в матричном виде систему из предыдущего примера

21.Схема применения правила Крамера при решении системы линейных уравнений

Правило Крамерa. Пусть задана система n линейных уравнений с n неизвестными вида

a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁,

a₂₁x₁+a₂₂x₂+…+a_2nx_n=b₂,

…………………………………….

a_n1x₁+a_n2x₂+…+a_nnx_n=b_n, (1)

или, в матричной форме, AX=B, где(m=n)обязательно!!!!

Правило Крамера. Если в системе (1) detA=Δ≠0, т.е. матрица А имеет обратную Матрицу А^-1,то система (1) имеет, и притом единственное, решение

X=A^-1B,

или, в покомпонентной записи,

x_i=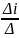 , i=1,2,…,n,

где Δi-определитель, получаемый из определителя Δ заменой i-го столбца на столбец свободных членов.

Пример: Решите систему уравнений

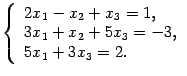
Выписываем матрицу системы

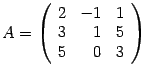и столбец свободных членов

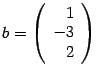
Находим определитель системы:

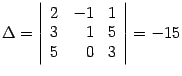Определитель отличен от нуля, следовательно, можно применить правило Крамера. Находим дополнительные определители:

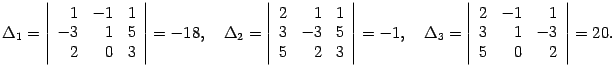
Итак,