8,9. Миноры и алгебраические дополнения

Если D = |A| - определитель порядка n, то минором M_ij элемента а_ij называют определитель порядка n-1, получающийся из D вычеркиванием i-й строки и j-го столбца. Под алгебраическим дополнением A_ij элемента а_ij понимают минор M_ij, домноженный на (-1)^i+j, т.е. A_ij = (-1)^i+jM_ij Например для определителя 3-го порядка:

D =

a11 a12 a13 a21 a22 a23 a31 a32 a32

Минор элемента а23 будет M23 =

a11 a12 a31 a32

Алгебраическим дополнением элемента а₂₃ будет A₂₃= (-1)²⁺³M₂₃= (-1)⁵M₂₃= -M₂₃ а для элемента а₁₃ , A₁₃= M₁₃ и т.п.

10. Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов ( Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n - ее порядком).

Сложение матриц 

     Суммой матриц   и   одинаковых размеров называется матрица   тех же размеров, у которой   Обозначение: C = А + В.

     Свойства сложения матриц: А + В = В + А, (А + В) + С = A + (B + C), А + 0 = A, А + (-A) = 0,   A, B, C.

Умножение матрицы на число 

     Произведением матрицы   на число   называется матрица   тех же размеров, у которой  Обозначение: 

     Свойства  ,       и 

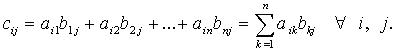11. Произведением матрицы   размером   на матрицу   размером   назвается матрица  размером   у которой   Обозначение: C = AB.

     Свойства AE = EA = A, AO = OA = O, (AB)D = A(BD),  (AB) = ( A)B = A( B), (A + B)D=AD + BD, D(A + B) = DA + DB (при условии, что указанные операции имеют смысл).

     Для квадратных матриц А и B, вообще говоря, 

12. Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

 Для того, чтобы построить обратную матрицу, необходимо

Найти определитель матрицы. Если этот определитель не равен нулю, то обратная матрица существует.

Найти алгебраические дополнения всех элементов матрицы: А11, А12, … ,Аnn

Из этих алгебраических дополнений построить матрицу в соответствии с указанными индексами

Транспонировать указанную матрицу

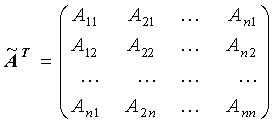
Разделив матрицу эту матрицу на определитель матрицы

Δ = det A

получим обратную матрицу

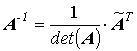
13. Алгоритм декомпозиции основан на идее представления исходной матрицы в виде произведения двух треугольных матриц. Пусть задана квадратная матрица:

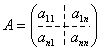
.  Представим A в виде:

A = BC,

где 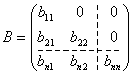   .  Тогда  .

14. Линейное, или векторное пространство   над полем P — это непустое множество L, на котором введены операции.

Определение n-мерного векторного пространства, данное в § 8, начиналось с определения n-мерного вектора как упорядоченной системы п чисел. Для n-мерных векторов были введены затем сложение и умножение на числа, что и привело к понятию n-мерного векторного пространства.

15. Система векторов A₁, A₂,...,A_n называется линейно зависимой, если существует ненулевой набор чисел λ_1, λ₂,...,λ_n,при котором линейная комбинация векторов λ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет ненулевое решение. Набор чисел λ_1, λ₂,...,λ_n является ненулевым, если хотя бы одно из чисел λ_1, λ₂,...,λ_n отлично от нуля.

Система векторов A₁, A₂,...,A_n называется линейно независимой, если линейная комбинация этих векторовλ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору только при нулевом наборе чисел λ_1, λ₂,...,λ_n, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет единственное нулевое решение.

Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)

Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.

Доказательство. Необходимость. Пусть система   линейно зависимая. Тогда, по определению, она представляет нулевой вектор нетривиально, т.е. существует нетривиальная линейная комбинация данной системы векторов равная нулевому вектору:

,

где хотя бы один из коэффициентов этой линейной комбинации не равен нулю. Пусть  ,  .

Разделим обе части предыдущего равенства на этот ненулевой коэффициент (т.е. умножим на  :

.

Обозначим:  , где  .

Тогда

или          ,

т.е. один из векторов системы линейно выражается через другие векторы этой системы, ч.т.д.

Достаточность. Пусть один из векторов системы линейно выражается через другие вектора этой системы:

.

Перенесем вектор   в правую часть этого равенства:

.

Так как коэффициент при векторе   равен  , то мы имеем нетривиальное представление нуля системой векторов  , что означает, что эта система векторов является линейно зависимой, ч.т.д.

Теорема доказана.

Следствие.

1. Система векторов векторного пространства является линейно независимой тогда и только тогда, когда ни один из векторов системы линейно не выражается через другие вектора этой системы.

2. Система векторов, содержащая нулевой вектор или два равных вектора, является линейно зависимой.

Доказательство.

1) Необходимость. Пусть система линейно независимая. Допустим противное и существует вектор системы линейно выражающийся через другие вектора этой системы. Тогда по теореме система является линейно зависимой и мы приходим к противоречию.

Достаточность. Пусть ни один из векторов системы не выражается через другие. Допустим противное. Пусть система линейно зависимая, но тогда из теоремы следует, что существует вектор системы линейно выражающийся через другие векторы этой системы и мы опять приходим к противоречию.

2а) Пусть система содержит нулевой вектор. Допустим для определенности, что вектор   : . Тогда очевидно равенство

,

т.е. один из векторов системы линейно выражается через другие вектора этой системы. Из теоремы следует, что такая система векторов является линейно зависимой, ч.т.д.

Заметим, что этот факт можно доказать непосредственно из определения линейно зависимой системы векторов.

Так как  , то следующее равенство очевидно

.

Это нетривиальное представление нулевого вектора, а значит система   является линейно зависимой.

2б) Пусть система имеет два равных вектора. Пусть для определенности  . Тогда очевидно равенство

, т.е. первый вектор линейно выражается через остальные векторы этой же системы. Из теоремы следует, что данная система линейно зависимая, ч.т.д.

Аналогично предыдущему это утверждение можно доказать и непосредственно определения линейно зависимой системы.

Действительно, так как  , то верно равенство

,

т.е. мы имеем нетривиальное представление нулевого вектора.

Следствие доказано.

Теорема (О линейной зависимости системы из одного вектора.

Система, состоящая из одного вектора является линейно зависимой тогда и только тогда, когда этот вектор нулевой.

Доказательство.

Необходимость. Пусть система   линейно зависимая, т.е. существует нетривиальное представление нулевого вектора

,

где   и  . Из простейших свойств векторного пространства следует, что тогда  .

Достаточность. Пусть система состоит из одного нулевого вектора  . Тогда эта система представляет нулевой вектор нетривиально

,

откуда следует линейная зависимость системы  .

Теорема доказана.

Следствие. Система, состоящая из одного вектора является линейно независимой тогда и только тогда, когда этот вектор ненулевой.

16.  Множество   называется подпространством линейного пространства V, если:

     1) 

     2) 

17.

 Ранг системы столбцов называется рангом этой матрицы.

 

Понятно, что строки тоже можно рассматривать как n-мерные векторы. Ранг системы строк, оказывается, равен рангу системы столбцов.