
- •1.Определение системы координат на прямой линии, и прямоугольных систем координат на плоскости и в пространстве.
- •2. Определение полярных координат на плоскости - . Связь полярных координат с координатами в прямоугольной системе координат.
- •4. Геометрический смысл и физический смысл линейных операций с векторами: сумма векторов , и умножение вектора на вещественное число .
- •Разностью a – b вектора a и вектор b называется такой вектор с, который в сумме с вектором b дает вектор a. (стр. 48 Аналитической Геометрии)
- •6. Операции над векторами
- •7.Определение линейной зависимости совокупности векторов , ,…, : привести два определения и показать их равносильность.
- •8.Определение базиса для векторов,расположенных на плоскости и в пространстве.Что значит базис ортогональный?
- •9.Определение,физический смысл и основные свойства скалярного произведения векторов а и b.Вычисление скалярного произведения.
- •10.Заданы векторы а и b.Как вычислить проекцию вектора а на направление определяемое вектором b?
- •11.Заданы векторы а и b.Как вычислить угол между a и b?
- •12.Определение,физический смысл и основные свойства векторного произведения векторов:a и b
- •13.Определение и основные свойства векторов a b c.Геометрический смысл смешанного произведения. Вычисление смешанного произведения векторов.
- •16. Вывод уравнения прямой на плоскости «в отрезках».
- •18.Нормирование общего уравнения прямой линии : . Получение выражения для вычисления отклонения произвольной точки от заданной прямой линии .
- •19. Вычисление расстояния от точки до прямой линии : .
- •20. Вычисление угла между двумя прямыми : и : .
- •22. Вывод уравнения плоскости, определяемой тремя точками: , , , не принадлежащими одной прямой.
- •23. Уравнение плоскости в отрезках.
- •24. Общее уравнение (полное) плоскости
- •25. Расстояние от точки , до плоскости, заданной уравнением , вычисляется по формуле:
- •26. Угол между плоскостями
- •27. Параметрическое уравнение прямой
- •Каноническое уравнение прямой
- •28. Уравнение прямой в пространстве, проходящей через две точки.
- •30. Угол между прямой и плоскостью.
- •Вопрос 31.
- •Вопрос 32.
- •Вопрос 33.
27. Параметрическое уравнение прямой
Направляющим вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
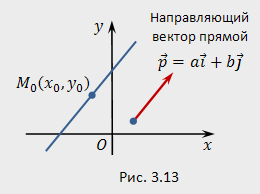
Пусть
на координатной плоскости
![]() заданы:
заданы:
а) точка ;
б)
ненулевой вектор
![]() (рис.3.13).
(рис.3.13).
Требуется
составить уравнение прямой, коллинеарной
вектору
![]() и
проходящей через точку
.
и
проходящей через точку
.
Выберем
на прямой произвольную точку
.
Обозначим
![]() и
и
![]() —
радиус-векторы точек
и
(рис.3.14).
—
радиус-векторы точек
и
(рис.3.14).
Точка
принадлежит
заданной прямой тогда и только тогда,
когда векторы
и
коллинеарны.
Запишем условие
коллинеарности:
![]() ,
где
,
где
![]() —
некоторое действительное число
(параметр). Учитывая, что
,
получим векторное
параметрическое уравнение прямой:
—
некоторое действительное число
(параметр). Учитывая, что
,
получим векторное
параметрическое уравнение прямой:
![]()
где
—
направляющий вектор прямой, а
![]() —
радиус-вектор точки, принадлежащей
прямой.
—
радиус-вектор точки, принадлежащей
прямой.

Координатная форма записи уравнения (3.11) называется параметрическим уравнением прямой
где
![]() —
координаты направляющего вектора
прямой.
Параметр
в
уравнениях (3.11),(3.12) имеет следующий
геометрический
смысл:
величина
пропорциональна
расстоянию от начальной точки
до
точки
—
координаты направляющего вектора
прямой.
Параметр
в
уравнениях (3.11),(3.12) имеет следующий
геометрический
смысл:
величина
пропорциональна
расстоянию от начальной точки
до
точки
![]() .
Физический
смысл
параметра
в
параметрических уравнениях (3.11), (3.12) —
это время при равномерном и прямолинейном
движении точки
по
прямой. При
.
Физический
смысл
параметра
в
параметрических уравнениях (3.11), (3.12) —
это время при равномерном и прямолинейном
движении точки
по
прямой. При
![]() точка
совпадает
с начальной точкой
точка
совпадает
с начальной точкой
![]() ,
при возрастании
движение
происходит в направлении, определяемым
направляющим вектором
.
,
при возрастании
движение
происходит в направлении, определяемым
направляющим вектором
.

Каноническое уравнение прямой
Выразим
параметр
из
каждого уравнения системы (3.12):
![]() ,
а затем исключим этот параметр:
,
а затем исключим этот параметр:
![]()
Уравнение
(3.13) называется каноническим
уравнением прямой.
В этом уравнении коэффициенты
![]() и
и
![]() не
равны нулю одновременно, так как это
координаты направляющего вектора
прямой.
не
равны нулю одновременно, так как это
координаты направляющего вектора
прямой.
28. Уравнение прямой в пространстве, проходящей через две точки.
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять уравнению прямой:
![]() .
.
Кроме того, для точки М1 можно записать:
![]() .
.
Решая совместно эти уравнения, получим:
![]() .
.
Это уравнение прямой, проходящей через две точки в пространстве.
29.
Пусть прямые
![]() и
и
![]() заданы каноническими уравнениями
заданы каноническими уравнениями
![]() и
и
![]() Очевидно,
угол между прямыми равен углу между
направляющими векторами этих прямых:
Очевидно,
угол между прямыми равен углу между
направляющими векторами этих прямых:
 Тогда
Тогда
|
|
Если
![]() то
то
![]()
Если
![]() ,
то
,
то
![]() или
или
![]()
![]() .
.
30. Угол между прямой и плоскостью.
Угол
между прямой
: и плоскостью
и плоскостью
 :
: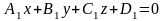 находиться в пределах от 0 градусов (в
случае параллельности) до 90 (в случае
перпендикулярности) . Синус этого угла
равен |cos¥|,
где ¥ - угол между направляющим
вектором прямой s
и нормальным вектором прямой n
плоскости. Вычисляя косинус угла между
векторами через координаты получим
находиться в пределах от 0 градусов (в
случае параллельности) до 90 (в случае
перпендикулярности) . Синус этого угла
равен |cos¥|,
где ¥ - угол между направляющим
вектором прямой s
и нормальным вектором прямой n
плоскости. Вычисляя косинус угла между
векторами через координаты получим
 ,
отсюда <ⱷ=arcsin
,
отсюда <ⱷ=arcsin
Вопрос 31.
Заданы прямая : и плоскость : . Найти их точку пересечения.
Запишем параметрический вид уравнения прямой



Подставим значения в уравнение плоскости
A1( )+B1(
)+B1( )+C1(
)+C1( )+D1=0
)+D1=0
A1x1+A1*t*a1x+B1y1+B1*t*a1y+C1z1+C1*a1z+D1=0
A1x1+B1y1+C1z1+D1=-A1*t*a1x-B1*t*a1y-C1*a1z
![]()
Это и есть t. Потом значение t подставляем в параметрические уравнения и получаем точку пересечения.

