
- •1.Определение системы координат на прямой линии, и прямоугольных систем координат на плоскости и в пространстве.
- •2. Определение полярных координат на плоскости - . Связь полярных координат с координатами в прямоугольной системе координат.
- •4. Геометрический смысл и физический смысл линейных операций с векторами: сумма векторов , и умножение вектора на вещественное число .
- •Разностью a – b вектора a и вектор b называется такой вектор с, который в сумме с вектором b дает вектор a. (стр. 48 Аналитической Геометрии)
- •6. Операции над векторами
- •7.Определение линейной зависимости совокупности векторов , ,…, : привести два определения и показать их равносильность.
- •8.Определение базиса для векторов,расположенных на плоскости и в пространстве.Что значит базис ортогональный?
- •9.Определение,физический смысл и основные свойства скалярного произведения векторов а и b.Вычисление скалярного произведения.
- •10.Заданы векторы а и b.Как вычислить проекцию вектора а на направление определяемое вектором b?
- •11.Заданы векторы а и b.Как вычислить угол между a и b?
- •12.Определение,физический смысл и основные свойства векторного произведения векторов:a и b
- •13.Определение и основные свойства векторов a b c.Геометрический смысл смешанного произведения. Вычисление смешанного произведения векторов.
- •16. Вывод уравнения прямой на плоскости «в отрезках».
- •18.Нормирование общего уравнения прямой линии : . Получение выражения для вычисления отклонения произвольной точки от заданной прямой линии .
- •19. Вычисление расстояния от точки до прямой линии : .
- •20. Вычисление угла между двумя прямыми : и : .
- •22. Вывод уравнения плоскости, определяемой тремя точками: , , , не принадлежащими одной прямой.
- •23. Уравнение плоскости в отрезках.
- •24. Общее уравнение (полное) плоскости
- •25. Расстояние от точки , до плоскости, заданной уравнением , вычисляется по формуле:
- •26. Угол между плоскостями
- •27. Параметрическое уравнение прямой
- •Каноническое уравнение прямой
- •28. Уравнение прямой в пространстве, проходящей через две точки.
- •30. Угол между прямой и плоскостью.
- •Вопрос 31.
- •Вопрос 32.
- •Вопрос 33.
13.Определение и основные свойства векторов a b c.Геометрический смысл смешанного произведения. Вычисление смешанного произведения векторов.
Определение.
Смешанным произведением упорядоченной
тройки векторов ![]() называется скалярное произведение
первого вектора на
векторное произведение
второго вектора на
третий и обозначается
называется скалярное произведение
первого вектора на
векторное произведение
второго вектора на
третий и обозначается
 .
.
Смешанное
произведение векторов
,
и
обозначается
![]() или
или
![]() .
.
Теорема: Смешанное произведение трех векторов равно объему параллелепипеда, построенного на векторах как на ребрах, взятому со знаком плюс
если
тройка правая, и со знаком минус, если
тройка левая. Действительно,
![]() ,
где φ -угол между векторами
и
,
а θ - угол между векторами
и
,
где φ -угол между векторами
и
,
а θ - угол между векторами
и
![]() .
Объем параллелепипеда, построенного
на векторах
,
и
,
равен произведению площади основания
.
Объем параллелепипеда, построенного
на векторах
,
и
,
равен произведению площади основания
![]() на высоту
на высоту
![]() .
Таким образом,
.
Таким образом,
первое утверждение доказано. Знак смешанного произведения совпадает со знаком cosθ, и поэтому смешанное произведение положительно когда
направлен в ту же сторону от плоскости векторов
и , что и вектор , т. е. когда тройка ,
, правая. Аналогично доказывается, что смешанное произведение левой тройки векторов отрицательно.
Смешанное произведение обладает следующими свойствами:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
14.Вывод
общего уравнения прямой на плоскости,
если задана точка
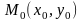 ,
принадлежащая этой прямой, и вектор
нормали
,
принадлежащая этой прямой, и вектор
нормали
 =
=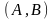 ,
перпендикулярный этой прямой.
,
перпендикулярный этой прямой.
Выберем
на плоскости произвольную точку ![]() .
Обозначим
.
Обозначим ![]() и
и ![]() —
радиус-векторы точек
и
—
радиус-векторы точек
и ![]() .
Точка
.
Точка ![]() принадлежит
заданной прямой тогда и только тогда,
когда векторы
принадлежит
заданной прямой тогда и только тогда,
когда векторы ![]() и
и ![]() перпендикулярны
(рис.3.5,б). Условие ортогональности
запишем при помощи скалярного произведения
(см. разд. 1.6.2):
перпендикулярны
(рис.3.5,б). Условие ортогональности
запишем при помощи скалярного произведения
(см. разд. 1.6.2):
![]()
Учитывая,
что ![]() ,
получаем векторное
уравнение прямой:
,
получаем векторное
уравнение прямой:
![]()
Это
уравнение можно записать в другой форме.
Преобразуем левую часть , используя
свойства скалярного произведения (см.
). Обозначая ![]() ,
получаем уравнение
,
получаем уравнение
![]() или
или ![]()
выражающее постоянство проекций на нормаль радиус-векторов точек, принадлежащих прямой.

Получим
координатную форму записи векторного
уравнения прямой (3.5). Так как ![]() и
и ![]() ,
по формуле (1.9) находим
,
по формуле (1.9) находим ![]() или
или
![]()
Полученное
соотношение (3.7) позволяет по координатам
точки
и
координатам ![]() нормали
записать
уравнение прямой без промежуточных
вычислений.
нормали
записать
уравнение прямой без промежуточных
вычислений.
Обозначив ![]() ,
получим уравнение
,
получим уравнение
![]()
15.Вывод
параметрических и канонического
уравнений прямой на плоскости, если
задана точка
,
принадлежащая этой прямой, и направляющий
вектор
= ,
параллельный этой прямой.
,
параллельный этой прямой.
Пусть
прямая l задана
точкой ![]() и
направляющим вектором
и
направляющим вектором ![]() (см.
рис. 11.5.2). Пусть M –
произвольная точка прямой.
(см.
рис. 11.5.2). Пусть M –
произвольная точка прямой.
|
|
Обозначим ![]() и
и ![]() радиус-векторы
точек
и M соответственно.
Вектор
радиус-векторы
точек
и M соответственно.
Вектор ![]() параллелен
прямой, и, следовательно, вектору
тогда
и только тогда, когда M лежит
на прямой. Так как
параллелен
прямой, и, следовательно, вектору
тогда
и только тогда, когда M лежит
на прямой. Так как ![]() то
то
|
Переменная t, принимающая различные значения, называется параметром, а уравнение – векторно-параметрическим уравнением прямой.
Если
ввести систему координат ![]() то
уравнение можно записать в виде
то
уравнение можно записать в виде
|
где ![]() и
и ![]() –
координаты точек
и M,
а
–
координаты точек
и M,
а ![]() –
координаты вектора
–
координаты вектора ![]() Отсюда следует, что
Отсюда следует, что
|
Эти уравнения называются параметрическими уравнениями прямой.
Пусть ![]() и
и ![]() тогда из уравнений следует, что
тогда из уравнений следует, что 
 и,
окончательно, уравнение
и,
окончательно, уравнение  которое называется каноническим
уравнением прямой,
с направляющим вектором
которое называется каноническим
уравнением прямой,
с направляющим вектором 



