Нормальный закон распределения

О непрерывной случайной величине говорят, что она распределена по нормальному закону распределения или является случайно распределенной, если плотность ее вероятности определяется формулой

. (5.17)

Здесь и  - среднее значение и среднее квадратичное отклонение случайной величины х.

В частном случае при = 0 эта плотность вероятности выражается функцией

. (5.18)

График этой функции представляет кривую вероятности. Он характеризуется следующими особенностями.

(1) Кривая пересекается с осью ординат в точке , являющейся точкой максимума этой функции.

(2) С осью абсцисс кривая не пересекается, и ось абсцисс является асимптотой к рассматриваемой кривой.

(3) Точками перегиба являются точки с координатами:

; .

Важно отметить, что большему значению  соответствует большая вытянутость кривой вдоль оси абсцисс и большее сжатие вдоль оси ординат, и наоборот. Это означает, что при большем значении  наблюдается больший разброс значений случайной величины относительно ее среднего значения.

Нормальное распределение играет большую роль в теории вероятностей.

Закон больших чисел

Особенно рельефно значение нормального распределения проявляется при большом числе случайных переменных.

Значение случайной величины может значительно отклоняться от ее математического ожидания (среднего значения), но среднее арифметическое большого числа отдельных значений случайной величины уже незначительно отклоняется от математического ожидания. При бесконечном увеличении числа переменных эти величины совпадают. А.М. Ляпунов сформулировал теорему, согласно которой если имеется n независимых случайных величин

x₁, x₂,…, x_i,…, x_n,

математическими ожиданиями

a₁,a₂,…,a_i,…, a_n

и дисперсиями

D(x₁), D(x₂),…, D(x_i),…, D(x_n),

Причем отклонения всех случайных величин от их математических ожиданий не превышают по абсолютной величине числа , т.е.

| x_i - a_i| ≤  ,

а все дисперсии ограничены числом C

D(x_i) ≤ C,

то при достаточно большом значении n сумма случайных величин x_i, будет иметь распределение, которое по мере возрастания числа n стремится к нормальному.

Мы примем эту теорему без доказательства. Кроме нее приведем также без доказательства два замечательных неравенства.

Неравенство Маркова. Если имеется случайная неотрицательная величина X , а  - произвольная положительная величина, то

P(0 ≤ X ≤ ) ≥ , (5.19)

где a = M(x).

Неравенство Маркова оценивает вероятность того, что значения случайной величины X не превосходят величины  < 0.

Пример применения неравенства Маркова. Пусть среднее число годных деталей, производимых ежемесячно в течение нескольких месяцев, равно 200. Определить вероятность того, что в данном месяце число годных деталей будет не более 220.

Решение. Применим для решения этой задачи неравенство Маркова. Тогда a = 200, а  = 220. И искомая вероятность равна

P(X ≤ 220) ≥ 1 – 200/220 ≥1 – 0.091 = 0.909.

Неравенство Чебышева. Другим полезным неравенством является неравенство Чебышева.

Если случайная величина X, имеющая математическое ожидание M(X) = a, а  - произвольное положительное число, то

(5.20)

и

. (5.21)

Пример применения неравенства Чебышева. Пусть среднее значение длины детали равно 50 см, а дисперсия равна 0.1. Пользуясь неравенством Чебышева оценить вероятность того, что изготовленная деталь окажется по своей длине не меньше 49.5 см и не более 50.5 см.

Решение. Здесь а = 50, а условие 49.5 ≤ Х ≤ 50.5 соответствует неравенству |X - a| ≤ 0.5. Таким образом,  = 0.5, а D(X) = 0.1. Тогда по неравенству Чебышева, имеет место

P(|X - a| ≤ 0.5) ≥ 1 – 0.1/0.25 = 0.6.

И, наконец, сформулируем без доказательства, теорему Чебышева.

Теорема Чебышева. Если дисперсия попарно независимых случайных величин не превосходит данного положительного числа C, то вероятность того, что абсолютное отклонение среднего арифметического таких величин от среднего арифметического их математических ожиданий меньше наперед заданного числа, с возрастанием количества случайных величин становится сколь угодно близкой к единице.

В важном частном случае, когда случайные величины x₁, x₂,…, x_i,…, x_n равные математические ожидания а и одинаково ограниченные дисперсии, можно утверждать, что соблюдается равенство

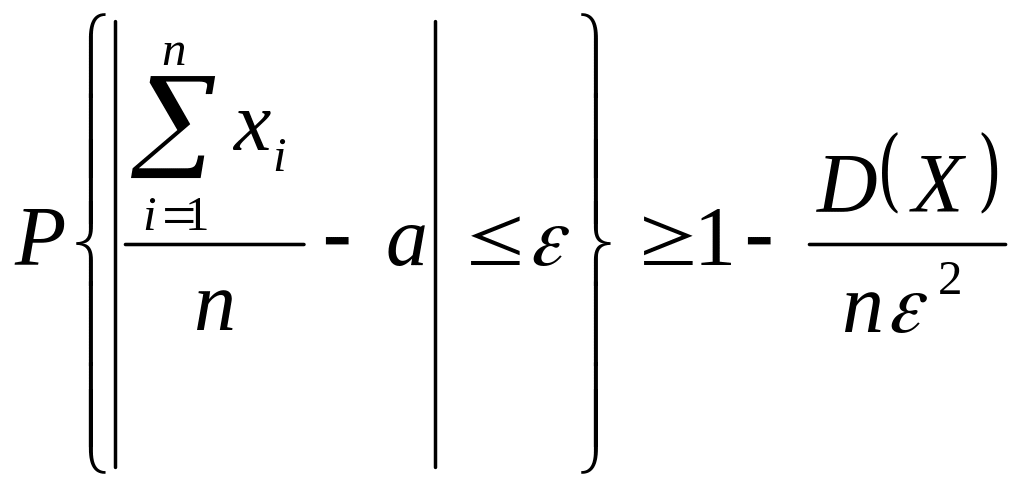. (5.22)

Запись теоремы Чебышева в применении к случайной величине числа появления события А в n (при достаточно большом числе) независимых повторных испытаниях принимает следующий вид:

. (5.23)

Доказанные теоремы и связанные с ними неравенства следует применять при поиске ответа на следующие вопросы:

(1) начиная с какого числа испытаний заданная вероятность отклонения будет находиться в требуемых границах;

(2) какова граница возможного отклонения случайной величины при заданных значениях n и P;

(3) при каком соотношении между объемами выборки и всей совокупности будет обеспечена заданная вероятность допустимого отклонения среднего значения по выборке от общего среднего значения.