43. Базис и размерность векторного пр-ва. 3 эквивалентных определения базиса.
Совокупность
векторов
называется базисом векторного пространства V, если выполнено одно из эквивалентных утверждений:
1. M –линейно независимая система образующих V.
2. M –максимальная (по числу векторов) линейно независимая система векторов в V.
3. M –минимальная (по числу векторов) система образующих пространства V.
Все
базисы
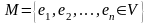пространства
V
над полем R, имеют одинаковое число
векторов. (УПР*)
Число векторов в базисе называется размерностью векторного пространства V и обозначается n=dim (V)=Card {M}
примеры нахождения базиса.
44. Координаты вектора в фиксированном базисе. Изменение координат вектора при замене базиса.
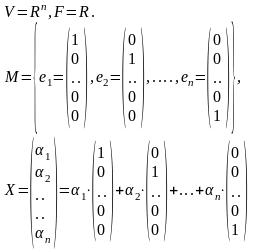
Пусть
дан
базис
векторного пространства
V
и вектор X
из V.
Координатами
вектора Х в этом базисе называют
коэффициенты в данном разложении
47.Сумма и пересечение подпространств. Формула для размерности подпространств, их суммы и пересечения.
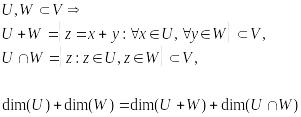
49. Геометрия в n – мерном пр-ве Rn
Скалярное произведение векторов.
Длина вектора.
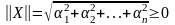
Угол между векторами. Неравенство Коши.
Ортогональные вектора.
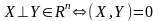
Ортонормальным базисом называется базис, состоящий из попарно ортогональных векторов, каждый из которых имеет длину равную единице.
50. Ортогональные матрицы и их св-ва.
- Ортогональная матрица – это квадратная матрица А, результат умножения которой на АТ равен единичной матрице.
св-ва: 1) Определитель ортогональной матрицы С равен +/- 1
2) Произведение ортогональных матриц есть ортогональная матрица
3) Единичная матрица Е ортогональна
4) Для ортогональной матрицы С обратная матрица сущ-ет и равна транспонированной матрице С
5) Для ортогональной матрицы С обратная матрица С-1 также ортогональна.
51. Ортогональное дополнение к подпр-ву в Rn
Ортогональным дополнением подпространства U из Rn
называется подпространство, состоящее из векторов,
ортогональных любому вектору из U.
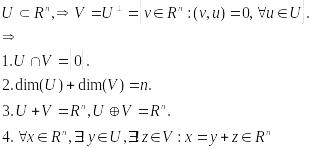
Ввещественные квадратичные формы.
55. Определение и св-ва веществ. квадратичных форм.
Квадратичной формой называется однородный многочлен f=f(x1, x2, … xn) второй степени от n переменных.
пример: x2+2y2+5z2-3xy+7xz-10yz
56. Матричная запись квадратичной формы. Преобразование матрицы кв.формы при линейной замене переменных.
Матричной записью квадратичной формы называется следующее выражение:
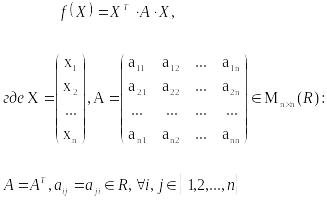
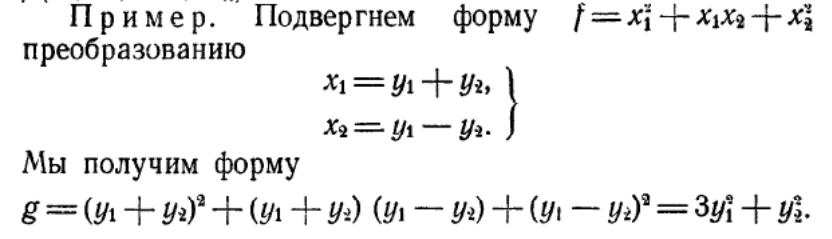
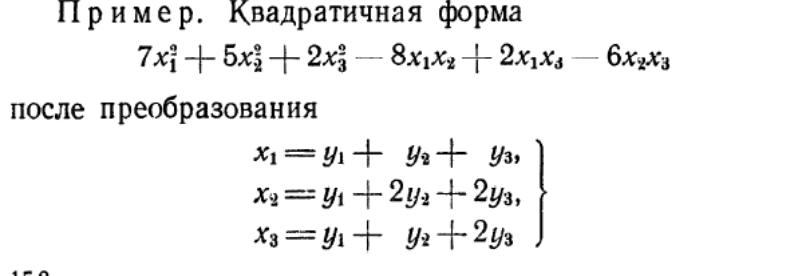
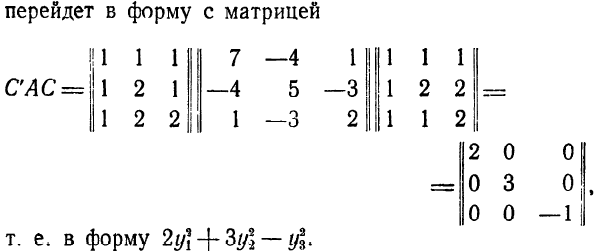
57. Теорема Лагранжа о приведении квадратичной формы к диагональному виду.
Любую вещественную квадратичную форму можно привести к диагональному виду невырожденным линейным преобразованием переменных, т.е. когда преобразованная квадратичная форма будет состоять только из квадратов новых переменных с некоторыми коэффициентами.
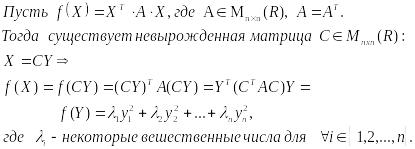
пример
58. Теорема об ортогональном приведении квадратичной формы к диагональному виду.
Любую вещественную квадратичную форму можно привести к диагональному виду при помощи линейного преобразования переменных с ортогональной матрицей.
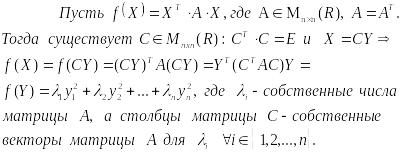
пример
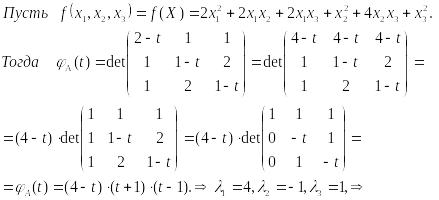
59. Определение и простейшие св-ва положительно определенных квадратичных форм.
Квадратичная форма называется положительно определенной, если все ее значения при вещественных значениях переменных, не равных одновременно нулю, положительны.
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы после приведения ее к диагональному виду все коэффициенты при квадратах новых переменных были положительны.
св-ва
60. Критерий Сильвестра
61. Закон инерции вещественных квадратичных форм.
Если вещественную квадратичную форму двумя способами привели к диагональному виду, то число квадратов новых переменных с положительными коэффициентами будет одинаково, так же как число квадратов новых переменных с отрицательными коэффициентами.
62. Задача о паре форм.
