Вопрос 19. Односторонние системы линейных уравнений.

Система m-линейных уравнений с n-неизвестными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:

a₁₁x₁+a₁₂x₂+…+a_1nx_n=0

a₂₁x₁+a₂₂x₂+…+a_2nx_n=0

…………………………………… (1)

a_m1x₁+a_m2x₂+…+a_mnx_n=0

Система линейных однородных уравнений всегда совместна, т.к. она всегда имеет хотя бы нулевые решения (0,0,…,0)

Если в системе (1) m=n, а ее определитель не равен 0, то такая система имеет только нулевое решение . Ненулевые решения, следовательно, возможны лишь для таких систем линейных однородных уравнений меньше числа переменных или при их равенстве, когда определитель системы равен 0.

Иначе система однородных линейных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэф-в при переменных меньше числа переменных, т.е. при r(A)<n .

Обозначим решение системы (1) x₁=k₁,…x_n=k_n в виде строки l₁=(k₁,k₁,…,k_n)

Решения системы линейных однородных уравнений обладают следующими свойствами:

1.Если строка l₁=(k₁,k₁,…,k_n)-решение системы (1 ), то и строка λl₁=(λk₁, λk₁,…, λk_n)-также решение этой системы.

2.Всякая линейная комбинация решений линейных однородных уравнений также является решением этой системы.

Система линейно независимых решений l₁,l₂,…,l_k называется фундаментальной, если каждое решение системы (1) является линейной комбинацией решений l₁,l₂,…,l_k.

Теорема: Если ранг r-матрицы коэффициентов при переменных системы линейных однородных уравнений (1) меньше числа переменных n, то всякая фундаментальная система решений системы (1) состоит из n-r решений.

Поэтому общее решение системы (1) линейных однородных уравнений имеет вид:

C₁l₁+C₂l₂+…+C_kl_k,

где l₁,l₂,…,l_k-любая фундаментальная система решений; C₁,C₂,…,C_k-произвольные числа, k=n-r

Вопрос 20 Расстояние м/у двумя точками. Площадь треугольника.

Для любых двух точек М(х₁;у₁), М₂(х₂;у₂). Расстояние: d=√x₂-x₁)²+(y₂-y₁)² (1)

Док-во:

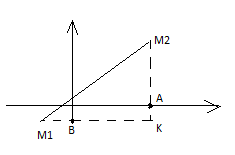
Опустим из точек M1 и M2 на оси Ox и Oy. Обозначим через K точку их пересечения. Легко видеть, что длина |M₁K|=|x₂-x₁| |M₂K|=|y₂-y₁|

Отсюда, по теореме Пифагора

d=√(M₁K)²+(M₂K)²=√(x₂-x₁)²+(y₂-y₁)²

Площадь треугольника

Для любых точек А(х1;у1) В(х2;у2) С(х3;у3), не лежащие на одной прямой площадь треугольника выч-ся по формуле

S=1/2((x2-x1)(y2-y1)-(x3-x1)(y3-y1)) (2)

Док-во:

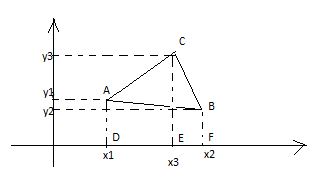
Площадь ABC:

S_ABC=S_ADEC+S_BCEF-S_ABFD (3)

Площадь трапеции S_ADEC= |DE|*(|AD|+|EC|)∕2= (x3-x1)(y3+y1)/2

S_BCEF=|EF|*(|EC|+|BF|)/2=(x2-x3)(y2+y3)/2

S_ABFD=|DF|*(|AD|+|BF|)/2=(x2-x1)(y1+y2)/2

Подставляя эти значения в (3) получим формулу (2)

S= 0.5/ |-(x2-x1)*(y2+y1)+(x2-x3)*(y2+y3)+(x3-x1)*(y3+y1)]| => (2)

Вопрос 21. Деление отрезка в данном отношении.

Пусть на плоскости задан М₁М_2.

И пусть М-любая точка этого отрезка , не совпадающая с концами

(4)

λ- отношение в котором точка М делит отрезок М1М2.

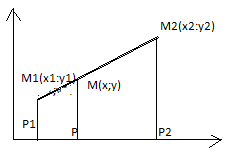
Задача о делении отрезка в данном отношении состоит в том, что по данному отношению λ и данным координатам М1 и М2 находятся координаты точки М

Теорема. Если точка М от (х;у) делит отрезок М1М2 в отношении λ, то координаты этой точки

, (5)

Доказательство:

Опустим перпендикуляр из точки М1, М и М2. Обозначим через Р1, Р, Р2-основания этих перпендикуляров. На основе теории о пропорц. отрез. прямой заключается между параллельными прямыми:

|P1P|=|X-X2|, |P-P2|=|X2-X|

Т.к. значение под модулем одинакового знака, то можно записать

=> => x=

Получить 2-ю из (5) аналогично, спроектировать координаты точки на ось у.

Если М-середина отрезка М1М2, то λ=1 и по формулам (5) координаты отрезка находятся формулой (5).