
- •Т 6 еорема Коши
- •Исследование функции
- •Комплексные числа
- •Свойство определенного интеграла
- •Условие существование определенного интеграла. Вычисление определенного интеграла.
- •Экстремумы функции нескольких переменных
- •Двойной и тройной интеграл их свойства и вычисления
- •Криволинейный интегралы. Формула Грина
П
5
Дифференциальные уравнения
О1 если функция
![]() имеет производную
имеет производную
![]() то эту функцию называют дифференцируемой
в данной точке.
то эту функцию называют дифференцируемой
в данной точке.
Если функция дифференциема в каждой точке отрезка (ab] или интервал (ab) то ее называют дифференциемой на отрезке или в интервале.
T-1 (необходимое условие существование производной)
Если функция
![]() дифференциема в некоторой точке
то она непрерывна в этой точке, имеет в
ней производные
дифференциема в некоторой точке
то она непрерывна в этой точке, имеет в
ней производные
Замечание обратное утверждение не верно!
![]()
функция не прерывна
на отрезке
![]()
![]()
![]()
![]()
![]()
дифференциал
Пусть
диффиренциема на отрезке (ab]
![]()
![]()
Опр произведение
![]() называют дифферинцалом функции f(х)
обозначают dy
dy=
называют дифферинцалом функции f(х)
обозначают dy
dy=![]()
рассмотрим функцию y=x
![]()
![]()
![]() производная функция
отличается от дифференциала на бесконечно
малую величину 2 порядка в приближенные
вычисления можно использовать формулу
производная функция
отличается от дифференциала на бесконечно
малую величину 2 порядка в приближенные
вычисления можно использовать формулу
![]()
![]() отсюда формула
приближоного вычисления
отсюда формула
приближоного вычисления
![]()
пример найти
![]() и
и
![]() для функции
для функции
![]()
а)для любого
значения б) для х=20
![]()
![]()
![]()
![]()
![]()
О
6
Теорема Роля
Если функция
![]() не прерывна на отрезке АВ и дифференциема
во всех точках отрезка и на концах
обращается в 0 то есть
не прерывна на отрезке АВ и дифференциема
во всех точках отрезка и на концах
обращается в 0 то есть
![]() то внутри отрезка АВ существует по
крайней мере одна точка С (А<C<B)
в которой f(x)=>0
f'(c)=0.(обращается
в ноль)
то внутри отрезка АВ существует по
крайней мере одна точка С (А<C<B)
в которой f(x)=>0
f'(c)=0.(обращается
в ноль)
Замечание 1. Теорема имеет простую геометрическую интерпретацию: между значениями а и b имеется по меньшей мере одно значение с такое, что в точке С (с, f(c)) графика функции касательная к графику параллельна оси Ох.
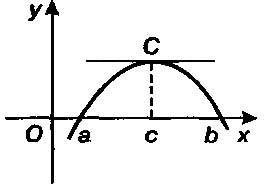
Замечание 2. Теорему можно сформулировать в более общем виде. Если у = f(x) - функция, дифференцируемая на отрезке [а, b] и f(а) = f(b), то между а и b найдется точка с, в которой производная равна нулю, т. е. f'(с) = 0.
Геометрический смысл роля
Докозательство
Если функция удовлетворяет условию теоремы то внутри отрезка [АВ] существует хотя бы 1 точка С которая паралельна оси ОХ.
1. Функция f(x)
постоянна на интервале [а,
b]; тогда
f ' (x) = 0
для любого x (a < x < b),
т.е. утверждение теоремы Ролля выполняется
автоматически.
2. Функция f(x)
не является постоянной (Рисунок 1); тогда
наибольшего или наименьшего или обоих
этих значений она достигает во внутренней
точке интервала, ибо f(b) = f(a),
и если f(a)
- наименьшее значение, то наибольшее
значение значение функция f(x)
примет внутри интервала. 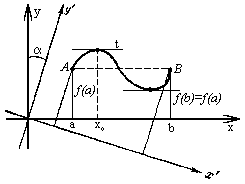
Пусть например f(x0) - наибольшее значение функции f(x) на интервале [а, b] и x0 - внутренняя точка этого интервала. Тогда f(x0) является максимумом функции: f(x0) > f(x) для всех x из достаточно малой окрестности x0 [за эту крестность можно впрочем, взять интервал (а, b)]. Так как, по условию, f(x) имеет в точке x0 производную, то по теореме о необходимом признаке экстремума,
f ' (x0) = 0,
и теорема Ролля доказана.
Теорема Ланганжа
Если функция
непрерывна на отрезки [ав] и дифферениема
во всех внутренних точках отрезка
надеться хотя бы одна точка С такая что
выполняет равенство
![]()
геометрический
смысл состоит в том что внутри отрезка
[АВ] надеться хотя бы одна точка С
которая параллельна секущей АВ.
![]()
![]()
![]()
С ледствие
1. Если производная функции равна нулю
в каждой точке некоторого промежутка,
то функция есть тождественная постоянная
в этом промежутке.
ледствие
1. Если производная функции равна нулю
в каждой точке некоторого промежутка,
то функция есть тождественная постоянная
в этом промежутке.
Следствие 2. Если две функции имеют равные производные в некотором промежутке, то они отличаются в этом промежутке лишь постоянным слагаемым.
Корнем (или нулем) функции у = f(x) называется такое значение х = х0 ее аргумента, при котором эта функция обращается в нуль. Геометрически корень функции означает абсциссу точки, в которой график функции пересекает ось их или касается ее.
Т 6 еорема Коши
![]() -пусть
функции не прерывны на отрезки [АВ] и
дифференцируемы на интервале (a, b) причем
-пусть
функции не прерывны на отрезки [АВ] и
дифференцируемы на интервале (a, b) причем
![]() ни где не принимает значение 0 тогда
найджеться такая точка С A<C<B
что величина равна
ни где не принимает значение 0 тогда
найджеться такая точка С A<C<B
что величина равна
![]()
Рассмотрим вспомогательную функцию Функция F(х) непрерывна на [a, b], дифференцируема на (a, b), причем F(а) = F(b) = 0. Следовательно, по теореме Ролля на (a, b) существует точка , такая, что F'() = 0:
Следовательно: Теорема доказана.
Теорема Ферма. Пусть функция f (х) определена на интервале (а, b) и в некоторой точке х0 (а, b) имеет локальный экстремум. Тогда, если в точке х0 существует конечная производная f '(x0), то f '(x0) = 0.
В точке х0 = 0 функция имеет минимум, но в этой точке производная не существует. Следовательно, теорема Ферма для данной функции неверна (не выполняется условие дифференцируемости функции в точке х0).
Исследование функции
Е
8-12
2 Если функция f(x) не прерывна на отрезке [ab] и дифференциема на нем причем f'(x)>0 а<x<b то функция возрастает на отрезке [ab] аналогична для убывания.
если f(x) убывает. [ab] то ее производная f'(x)<=0 на отрезке [ab]
max-функция
называется тогда
![]() если в некоторой окрестности этой точки
для всех точек кроме
если в некоторой окрестности этой точки
для всех точек кроме
![]() выполняется
не равенство
выполняется
не равенство
![]()
min-функция
называется тогда
если в некоторой окрестности этой точки
для всех точек кроме
выполняеться
не равенство
![]()
max и min называют точками экстремума или экстремальными значениями
Теорема
дифференцируемая функция
![]() имеет в точке
max
или min
то ее производная в этой точке равна 0
имеет в точке
max
или min
то ее производная в этой точке равна 0
точки экстремума нужно искать в тех точках которая равна 0 либо не существует.
Пример
![]()
![]()
![]() существует всюду
существует всюду
![]() в точке х=0 хотя производная =0 но эта
точка не является экстремумом.
в точке х=0 хотя производная =0 но эта
точка не является экстремумом.
Теорема достаточная теорема.
пусть функция
не прерывна в точке х=0 тогда если
производная
![]()
![]()
![]()
![]() -то
точка минимум
-то
точка минимум
если
![]()
![]() -то
точка максима
-то
точка максима
Наибольшее значение функции на отрезке пусть функция f(x) не прерывна на отрезке [ab]тогда на этом отрезке [ab] она принимает наибольшее и наименьшее значение
наибольшее и наименьшее значение на отрезке а и в функция принимает либо в одном из экстремумов либо в одном из его концах.
вогнутость и выпуклость
Пусть имеет производную (ab) если график кривой на промежутке [ab] расположен выше любой касательной проведя в точке этом промежутке то функция называется вогнутой на этом промежутке (выгнутой вниз)
Пусть имеет производную (ab) если график кривой на промежутке [ab] расположен ниже любой касательной то функция называется выпуклой на этом промежутке (выгнутой в веепх)
точка перегиба
если 2 промежутка
![]() и
и
![]() то на одной функция вогнута на другой
выпукла
то на одной функция вогнута на другой
выпукла
Если
![]() >0
на промежутке (ab)
то на этом промежутке функция вогнута
>0
на промежутке (ab)
то на этом промежутке функция вогнута
Если <0 на промежутке (ab) то на этом промежутке функция выгнута
Если =0 или не существует и точка вторая производная меняет знак то точка перегиба.
Прямая называется асимптотой если расстояние от кривой до этой прямой при увеличении в бесконечности стремиться к 0.
верти кальная
асимптота
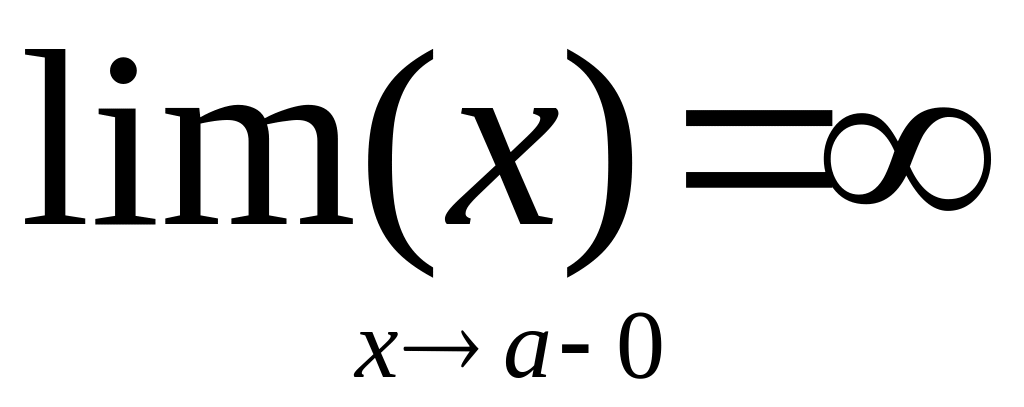
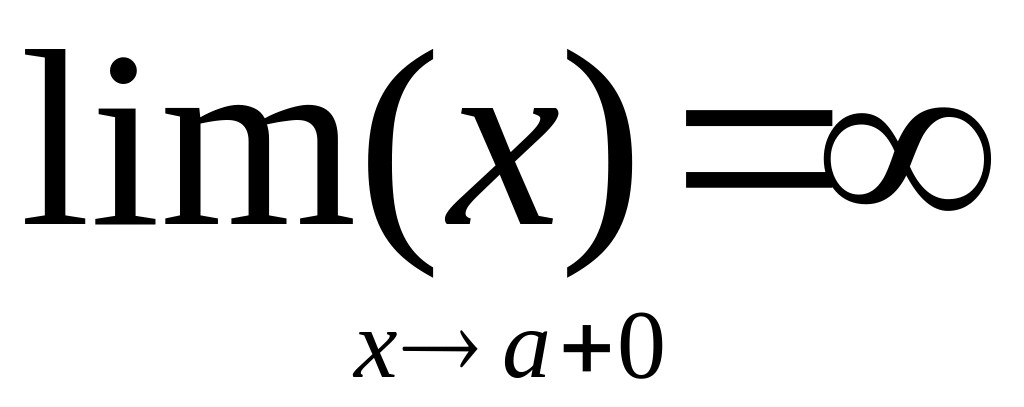 то x=a
это асимптота
то x=a
это асимптота
наклонная асимптота
пусть функция
имеет наклонную асимптоту
![]()
![]()
![]()
