Вопрос 18 Метод Гаусса.

Рассмотрим решение системы m-линейных уравнений с n-переменными в общем виде.

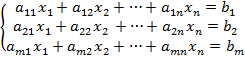(1)

Метод Гаусса-метод последовательного исключения переменных заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных , находятся все остальные переменные.

Предположим, что в системе (1) коэффициент при переменной x₁ в первом уравнении a₁₁≠0 (если это не так, то этого можно добиться перестановкой уравнений местами).

Шаг 1. Умножая первое уравнение на числа -a₂₁/a₁₁, -a₃₁/a₁₁,…,-a_m1/a₁₁ и прибавляя полученные уравнения соответственно ко второму, третьему,…,m-му уравнению системы (1), исключим переменную x₁ из всех последующих уравнений, начиная со второго. Получим:

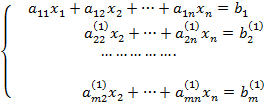(2)

Где буквами с верхним индексом ⁽¹⁾ обозначены новые коэффициенты, полученные после первого шага.

Шаг 2.Преположим, что a22(1)≠0. Умножая второе уравнения на числа –a₃₂⁽¹⁾/a₂₂⁽¹⁾, --a₄₂⁽¹⁾/a₂₂⁽¹⁾,…,-- a_m2⁽¹⁾/a₂₂⁽¹⁾ и прибавляя полученные уравнения соответственно к третьему, четвертому,.., m-му уравнению системы (2), исключим переменную x₂ из всех последующих уравнений, начиная с третьего.

Продолжая процесс последовательного исключения переменных x₃,x₄,…,x_r-1,после (r-1)-го шага получим систему:

a₁₁x₁+a₁₂x₂+…+a_1rx_r+…+a_1nx_n=b₁

a₂₂⁽¹⁾x₂+…+ a_2r⁽¹⁾x_r+…+a_2n⁽¹⁾x_n=b₂⁽¹⁾… (3)

a_r^(r-1)+…+a_rn^(r-1)x_n=b_r^(r-1)

0=b_r+1^(r-1)

0=b_n^(r-1)

Число ноль а последних m-r уравнениях означает, что их левые части имеют вид O*x₁+O*x₂+…+O* x_m . Если хотя бы одно из чисел b_r+1,…,b_m^(r-1) не равно нулю, то соответствующее равенство противоречиво, и система (1) несовместима.

Т.о., для любой совместной системы числа b_r+1^(r-1),…,b_m^(r-1) В системе (3) равны нулю. В этом случае последние m-r уравнений в системе (3) являются тождествами и их можно не принимать во внимание при решении системы (1). Очевидно, что после отбрасывания «…» уравнений возможны два случая: а)число уравнений системы (3) равно числу переменных, т.е. r=n. В этом случае, система (3) имеет треугольный вид; б)r<n, в этом случае система (3 ) имеет ступенчатый вид.

Переход от системы (1) к равносильной системе (3) называется прямым ходом метода Гаусса, а нахождение переменных из системы (3)-обратным ходом.

Преобразования Гаусса удобно проводить, осуществляя преобразованная не с самими уравнениями, а с матрицей их коэффициентов. Для этого рассматривают матрицу:

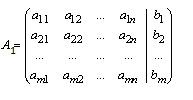
называемую расширенной матрицей системы (1) , т.к. в нее дополнительно включен столбец из свободных членов.

Запрос о разрешимости системы (1) в общем виде рассматривается в ……

Теорема Кронекера – Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

Для совместных систем линейных уравнений верны следующие теоремы:

1.Если ранг матрицы совместной системы равен числу переменных, т.е r=n, то система (1) имеет единственное решение.

2.Если ранг матрицы совместной системы меньше числа переменных, т.е r<n, то система (1) неопределенная и имеет бесконечное множество решений.

2 вариант. Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.

Система т линейных уравнений с п неизвестными имеет вид:

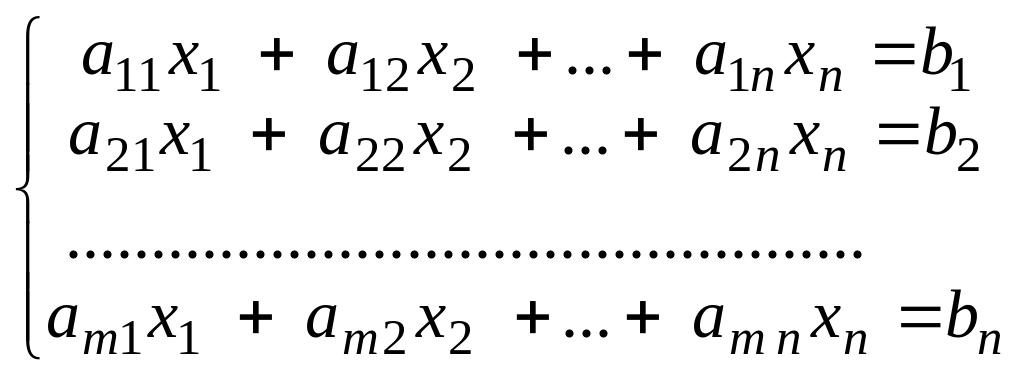
x₁ , x₂, …, x_n – неизвестные.

a_{i j} - коэффициенты при неизвестных.

b_i - свободные члены (или правые части)

Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.

Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными, если они имеют одно и то же множество решений.

К элементарным преобразованиям системы отнесем следующее:

1. перемена местами двух любых уравнений;

2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Элементарные преобразования переводят систему уравнений в равносильную ей.

Элементарные преобразования системы используются в методе Гаусса.

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

Дана система:

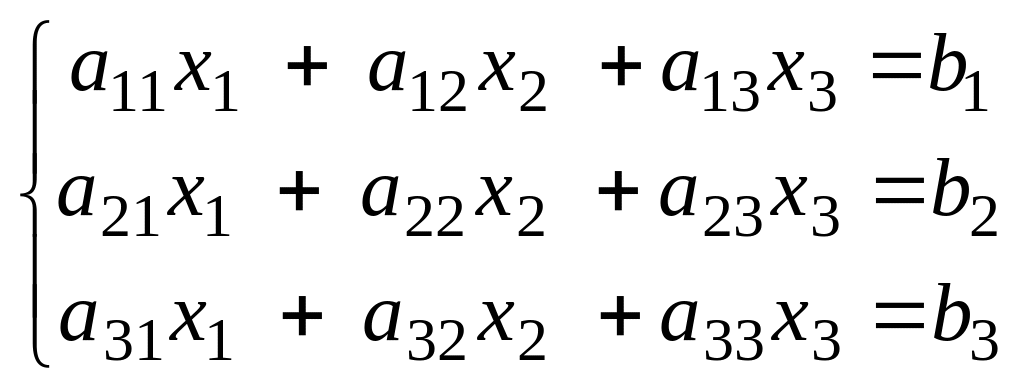( 1 )

1-ый шаг метода Гаусса.

На первом шаге исключим неизвестное х₁ из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а₁₁. Получим уравнение:

( 2 )

где

Исключим х₁ из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х₁ (соответственно а₂₁ и а₃₁).

Система примет вид:

( 3 )

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

2-ой шаг метода Гаусса.

На втором шаге исключим неизвестное х₂ из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:

( 4 )

где

Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:

Предполагая, что находим

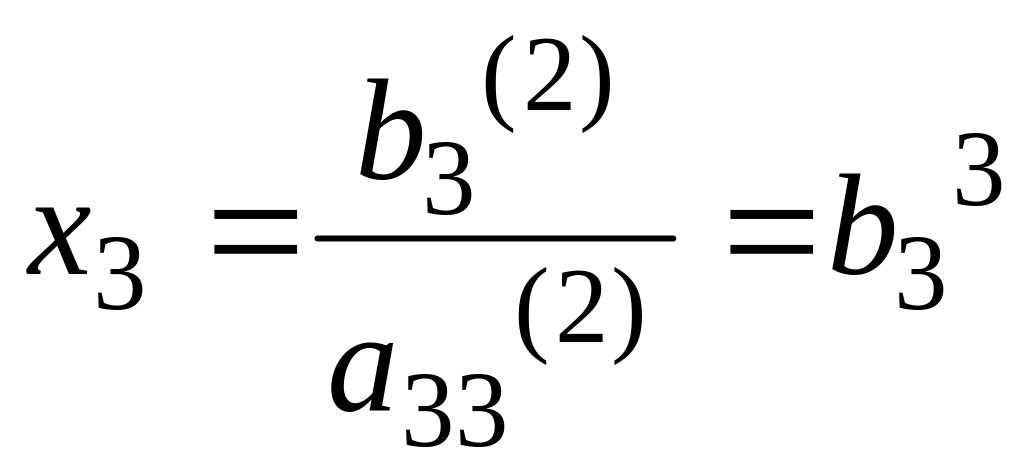
В результате преобразований система приняла вид:

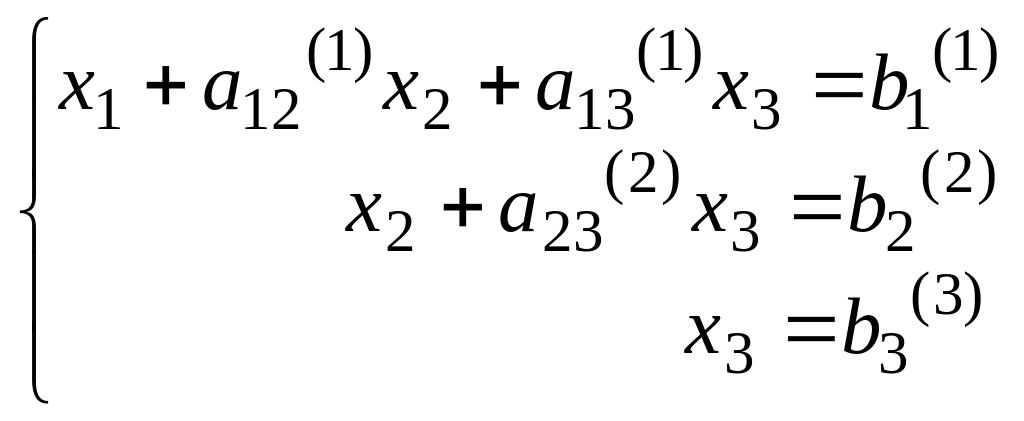(5)

Система вида (5) называется треугольной.

Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.

Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.

Для этого найденное значение х₃ подставляют во второе уравнение системы (5) и находят х₂. Затем х₂ и х₃ подставляют в первое уравнение и находят х₁.

В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.

Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.

Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b  0, то это означает, что система несовместна и решений не имеет.

В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.

Треугольная система имеет вид:

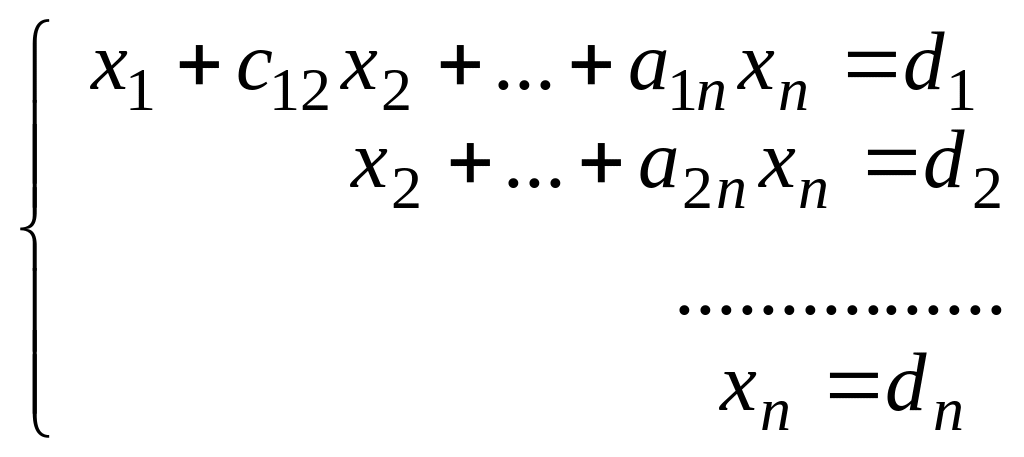
Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.

Ступенчатая система имеет вид:

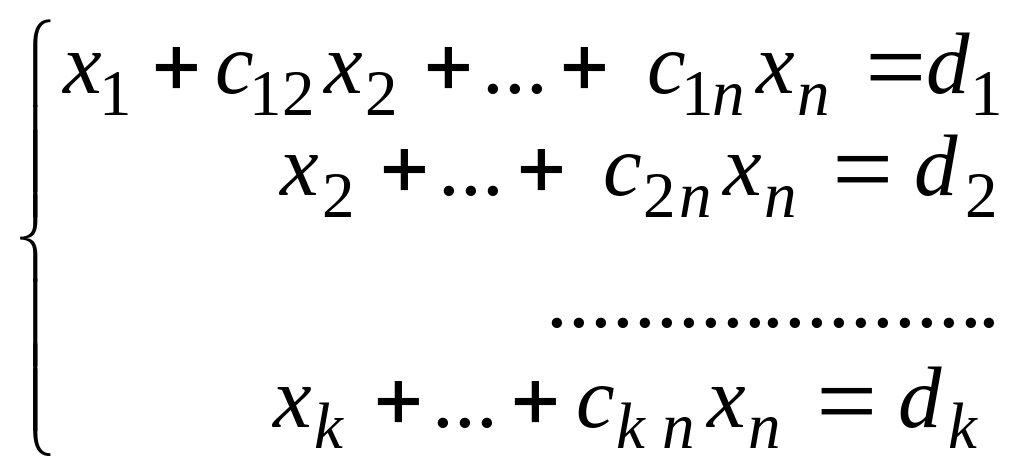
Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными х_k+1, … , x_k переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х₁, … , x_k, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.

Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.