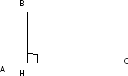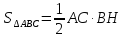- •Логико-дидактический анализ темы «площади параллелограмма, треугольника и трапеции».
- •I. Обзор математической и методической литературы по теме.
- •III. Анализ задачного материала. Смотреть очень неудобно, ключевые задачи нужно приводить сразу в группе, к которой она относится. И потом не в каждой же группе только одна ключевая задача
- •Рассмотрим треугольники abd и acd. Эти треугольники имеют равные высоты и общее основание. Следовательно, их площади равны: (*).
- •IV. Постановка учебных задач и диагностируемых целей.
- •V. Разработка конспекта урока по теме «Площади параллелограмма, треугольника и трапеции».
- •Ход урока
Клокова Анна, Максимова Мария 341 группа ФМИФ
Логико-дидактический анализ темы «площади параллелограмма, треугольника и трапеции».
Геометрия: Учеб. для 7-9 кл. сред. шк./ Л. С. Атанасян и др. – М.: Просвещение, 1990 (Глава VI, §2).
ОСНОВНОЕ СОДЕРЖАНИЕ ПРОЕКТА.
I. Обзор математической и методической литературы по теме.
Обзор методической литературы
-
В помощь учителю математики: Метод. рекомендации по диагностике развития учащихся 8 – х классов при обучении математике. Н. Н.:НГПУ, 1997 (стр. 49-65: анализ теоретического и задачного материала, выделены диагностируемые цели, представлены математические положения, входящие в основу метода разбиения-дополнения, выделяются три основных приема метода площадей, тестовые задания для проверки знаний учащихся).
-
Теория и методика обучения математике в средней школе. Учебное пос. для студ. мат. спец. пед. вузов, под. ред. Т. А. Ивановой. Изд. 2-е, испр. и доп. Н. Н.: НГПУ, 2009 (стр. 176-179: рассмотрены группы задач по нашей теме, в каждой из которых выделены ключевые задачи; описаны, какого уровня сложности задачи в группах; выделены этапы в обучении школьников решению задач при изучении нашей темы).
-
Изучение геометрии в 7-9 классах. Пособие для учителей. Атанасян Л.С. и др. М.: Просвещение, 2009.
Пособие предназначено для учителя, который преподает геометрию в 7-9 классах по учебнику авторов: Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. Оно написано в соответствии с методической концепцией этого учебника, полностью соответствует ему как по содержанию, так и по структуре. Пособие будет полезно в первую очередь начинающему учителю.
На стр. 99-103 данного пособия представлен следующий материал по теме «Площадь параллелограмма, треугольника, трапеции». Назначение данной темы; рекомендации по изложению теоретического материала ученикам; изучение параграфа распределено по урокам; с/р обучающего характера (I, II варианты) и III вариант для более подготовленных учащихся; представлены задачи (устного характера); требования к учащимся.
-
Гаврилова Н.Ф. Поурочные разработки по геометрии: 8 класс. - 2-е изд., перераб. и доп. - М.: ВАКО, 2010, 368 с. (В помощь школьному учителю).
Пособие представляет собой подробное поурочное планирование по геометрии для 8 класса общеобразовательных учреждений. Издание ориентировано прежде всего на работу с базовым учебником Л.С. Атанасяна и др. Геометрия: 7-9 кл. (М.: Просвещение). Особенностью пособия является дифференцированный подход к планированию, позволяющий проводить уроки в классах разного уровня подготовки - от классов гуманитарного профиля и коррекционных до специализированных физико-математических. Пособие полностью автономно и не требует привлечения каких-либо дополнительных материалов, может быть использовано учителями, работающими с другими учебниками по геометрии, например А.Г. Погорелова.
В данной книге объяснено значение теоремы об отношении площадей треугольников, имеющих по равному углу; разработаны примерные уроки по теме «Площадь параллелограмма, треугольника трапеции», а именно, площадь многоугольника (урок 17), площадь параллелограмма (19 урок), площадь треугольника (урок 20, урок 21), площадь трапеции (урок 22, урок 23); решение задач на вычисление площадей фигур.
-
Геометрия. 8 класс. Дидактические материалы. Зив Б. Г., Мейлер В. М. 13-е изд. М.: Просвещение, 2010 (тесты С-10, С-11, С-12 по теме «Площадь параллелограмма, треугольника и трапеции» изо всех вариантов)
-
Геометрия в таблицах. 7-11 класс. Справочное пособие. Л. И. Звавич, А. Р. Рязановский (стр 16, 24, 26)
В таблице 4. Треугольник представлены чертеж, формулы площади треугольника (в частности, прямоугольного), в таблице 5. Параллелограмма представлены чертеж, формулы площади параллелограмма, в таблице 6. Трапеция представлены чертеж, формулы площади трапеции.
-
Геометрия: Дополнительные главы к школьному учебнику 8 класса: Учебное пособие для учащихся школ и классов с углубленным изучением математики / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. – М.: Просвещение, 1996 (50-54, 57-65 стр: задачи повышенной трудности)
Настоящее пособие является дополнением к учебнику «Геометрия», 7-9 авторов Л.С. Атанасян, В.Ф. Бутузов и др. (М.: Просвещение, 1990 и последующие издания). Оно полностью соответствует программе углубленного изучения математики. Книга может быть использована также в классах общеобразовательных учреждений для индивидуальной работы с учащимися, проявляющими интерес к математике.
-
Великина П. Я. Сборник задач по геометрии для 6—8 классов. Пособие для учителей. Изд. 2, переработ. и доп. М., «Просвещение», 1971(стр. 38-41: задачи разного уровня сложности, включая устные задачи, приведена практическая задача)
Данный сборник предназначен не только тренировать учащихся в усвоении программного материала, но и развивать их сообразительность, находчивость, конструктивные способности и математическое мышление. С его помощью посредством задач учащиеся познакомятся с идеями движения, соответствия и функциональной зависимости и тем самым школьный курс геометрии несколько приблизится к современной геометрии. Каждая тема сборника содержит устные упражнения и задачи, решение которых экономит время урока и развивает внимание учащихся.
-
Зив Б. Г. Задачи к урокам геометрии. 7-11 классы. – С. П., 1998 (стр. 144-151: задачи разного уровня сложности: от самых простых (для совсем слабых учеников, варианты 1 и2) до задач, которые можно использовать на кружковых занятиях по математике (варианты 7 и 8);это задачи для работы как на уроках, так и дома)
Обзор математической литературы
-
Бронштейн И. Н. Справочник по математике. М.: Наука, 1986 (2.6.1. Планиметрия)
Основные формулы с пояснениями собраны в один параграф. Приведены рисунки и подробный разбор примеров на применение данных формул.
-
Выгодский М. Я. Справочник по элементарной математике. М.: Астрель; АСТ, 2001 (§21)
В этом пособии собраны важнейшие формулы для вычисления площадей плоских фигур.
-
Крамор В. С. Повторяем и систематизируем шк. курс геометрии. М.: Просвещение, 1992
Представлен справочный материал, задачи с решениями, контрольные вопросы по теме для самопроверки.
5 баллов
II. Анализ теоретического материала.
Выделение и общий анализ ОДЕ темы (аксиомы; понятия и их определения; теоремы – их формулировки и доказательства; правила).
п. 51. Площадь параллелограмма
-
понятия высоты параллелограмма.
Вводится через род и видовые отличия.
Перпендикуляр (род), проведенный из любой точки противоположной стороны к прямой, содержащей основание (видовое отличие), называется высотой параллелограмма.
Параллелограмм имеет две различные высоты. Знание этого факта необходимо для применения метода площадей к решению задач.
-
теорема о площади параллелограмма.
Площадь параллелограмма равна произведению его основания на высоту.
Условие: параллелограмм, заключение: площадь равна произведению основания параллелограмма на его высоту. Теорема-свойство; форма формулировки – категоричная, простая. Можно представить эту теорему в условной форме: если данная фигура является параллелограммом, то её площадь равна произведению её основания на высоту.
В основе доказательства – метод разбиения/дополнения проводятся две высоты, т. о. теорема сводится к теореме о площади прямоугольника, применяется свойство о том, что равносоставленные фигуры равны по площади); также используются основные свойства площади, признак равенства прямоугольных треугольников (по гипотенузе и острому углу).
п. 52. Площадь треугольника
Понятие высоты треугольника давалось во второй главе. Здесь это понятие используется, т. е. присутствуют внутрипредметные связи.
У треугольника три различные высоты. Знание этого факта необходимо для применения метода площадей к решению задач.
-
теорема о площади треугольника
Площадь треугольника равна половине произведения его основания на высоту.
Условие теоремы: треугольник, заключение: формула площади треугольника. Теорема-свойство; форма формулировки – категоричная, простая. Можно представить эту теорему в условной форме: если данная фигура является треугольником, то её площадь равна половине произведения её основания на высоту.
Основа доказательства – метод разбиения/дополнения (треугольник достраивается до параллелограмма). Применяются основные 2 свойства площади, третий признак равенства треугольников, теорема о площади параллелограмма.
-
два следствия из теоремы:
-
Площадь прямоугольного треугольника равна половине произведения его катетов.
-
Если высоты двух треугольников равны, то их площади относятся как основания.
Второе следствие порождает один из приемов метода площадей.
Оба следствия в учебнике приводятся без доказательства.
Доказательство следствий.
Следствие 1.
Площадь прямоугольного треугольника равна половине произведения его катетов.
|
Дано:
угол C – прямой Доказать:
|
|
Доказательство.
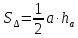 (1)
(1)
Т.
к. треугольник ABC
прямоугольный с прямым углом C,
то
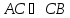 .
.
Если
взять в качестве основания
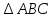 сторону CB,
то сторона AC
будет высотой, проведенной к выбранному
основанию. Тогда по формуле (1) имеем:
сторону CB,
то сторона AC
будет высотой, проведенной к выбранному
основанию. Тогда по формуле (1) имеем:
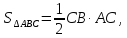
где
CB
и AC
– катеты
 ABC.
ABC.
Что и требовалось доказать.
Следствие 2.
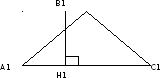
Если высоты двух треугольников равны, то их площади относятся как основания.
|
Дано:
B1H1
– высота
BH
– высота
B1H1= BH (1)
Доказать:
|
|
|
Доказательство.
|
|
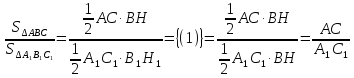
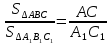
Что и требовалось доказать.
-
теорема об отношении площадей треугольников, имеющих по равному углу
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные стороны.
Теорема – свойство. Теорема простая, формулировка условная.
Доказательство основано на наложении одного треугольника на другой и использовании второго следствия из теоремы о площади треугольника.
Данная теорема является основой для доказательства первого признака подобия треугольников, которое рассматривается в главе VII. Т. е. эта теорема осуществляет внутрипредметные связи. Эта теорема также порождает один из приемов метода площадей.
п. 53. Площадь трапеции
В данном пункте идет речь о вычислении площади произвольного многоугольника. Так, для вычисления площади произвольного многоугольника обычно поступают так: разбивают многоугольник на треугольники и находят площадь каждого треугольника. Сумма площадей этих треугольников равна площади данного многоугольника.
-
понятие высоты трапеции
Вводится формально-логически.
Условимся называть высотой трапеции перпендикуляр (род), проведенный из любой точки одного из оснований к прямой (видовое отличие), содержащей другое основание.
У трапеции по величине только одна высота.
теорема о площади трапеции
Площадь трапеции равна произведению полусуммы её оснований на высоту.
Условие теоремы: трапеция, заключение: формула площади трапеции. Теорема-свойство; форма формулировки – категоричная, простая. Можно представить эту теорему в условной форме: если фигура является трапецией, то её площадь равна произведению полусуммы её оснований на высоту.
Основа доказательства: метод разбиения (трапеция «разбивается» диагональю на два треугольника), второе основное свойство площадей, формула площади треугольника.
ОБЩИЕ ВЫВОДЫ.
В §2 главы VI рассматриваются следующие дидактические единицы.
Понятия (термины, символы): высоты параллелограмма, треугольника и трапеции.
Основания параллелограмма, треугольника и трапеции вводятся через обозначения.
Теоремы: о площадях частных видов многоугольников (параллелограмма, треугольника, трапеции) и следствия из них; теорема об отношении площадей треугольников, имеющих равные углы.
Формулы для вычисления площадей параллелограмма, треугольника и трапеции выводятся на основания свойств площадей и следствий из них. Значит, в процессе обучения нужно создать такие условия, в которых ученик не только сможет запомнить эти формулы, будет учиться их применять в различных задачных ситуациях, но и осознает генетически исходную связь между ними. Каждая следующая формула связана с предыдущей.
При доказательстве теорем о площадях частных видов многоугольников учащиеся впервые встречаются с новым для них методом «разбиения и дополнения». Выделение этого метода и анализ условий его применения будет способствовать осознанию необходимости и сущности дополнительных построений в процессе поиска решения задач, сводящихся к установлению соотношений между площадями многоугольников.
Выделим некоторые математические положения, которые лежат в основе метода «разбиения и дополнения».
В основе приема «разбиения» лежат следующие, не доказываемые в школе математические положения.
-
Если многоугольник М разбить на многоугольники М1, М2, …, Мn, далее сконструировать из них фигуру N, то
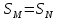 (т.
е. равносоставленные фигуры равновелики).
(т.
е. равносоставленные фигуры равновелики). -
Если многоугольник N разбить на многоугольники двумя различными способами:
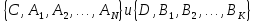 ,
то из равенства
,
то из равенства
 будет
следовать равенство
будет
следовать равенство
 .
. -
Если многоугольник М разбить на многоугольники
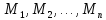 ,
а многоугольник N
– на многоугольники
,
а многоугольник N
– на многоугольники
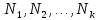 ,
то из равенства
,
то из равенства
 будет
следовать равенство
будет
следовать равенство
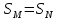 .
.
Выделим некоторые математические положения, на которых основано применение приема «дополнения».
-
Если многоугольник М дополнить равновеликими с ним многоугольниками
 до
многоугольника N,
то
до
многоугольника N,
то
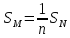 .
. -
Если многоугольник А дополнить многоугольниками
 до
фигуры M,
а многоугольник В дополнить многоугольниками
до
фигуры M,
а многоугольник В дополнить многоугольниками
 до
фигуры N
таким образом, чтобы выполнялись условия
(1)
до
фигуры N
таким образом, чтобы выполнялись условия
(1)
 и (2)
и (2)
 ,
тогда
,
тогда
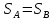 .
.
10 баллов

 ABC
– прямоугольный
ABC
– прямоугольный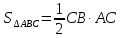

 ABC,
ABC,
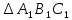

 ABC
ABC