Вопрос 40. Коррелированность и зависимость случайных величин.

Две случайные величины X и Y называются коррелированными, если их корреляционный момент ( или коэффициент корреляции) отличен от нуля; Х иY некоррелированные, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы. Действительно, если предположить противное, получается, что , а это прочиворечит условию, т.к. для коррелированных величин . Обратное предположение не всегда имеет место, т.е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Корреляционный момент двух зависимых величин может быть не равен нулю, но может и быть = 0. Рассмотрим пример, убедимся, что две зависимости величины могут быть некоррелированными.

Пример: Двумерная случайная величина (X,Y) задана плотностью распределения:

внутри эллипса

вне этого эллипса

Доказать, что X и Y – зависимые некоррелированные величины.

Решение: Воспользуемся ранее вычисленными плотностями распределения составляющих X и Y.

внутри заданного эллипса и вне его. Так как ,то X и Y – зависимые величины. Для того, чтобы доказать некоррелированность X и Y, достаточно убедиться в том, что . Найдем корреляционный момент по формуле:

. Поскольку функция f(x) симметрична относительно оси Оу, то М(Х)=0; аналогично М(Y)=0 в силу симметрии f(y) относительно оси Ох. Следовательно, . Вынося постоянный множитель f(x,y) за знак интеграла, получается. Внутренний интеграл равен нулю (подынтегральная функция нечетная, пределы интегрирования симметричны относительно начала координат), следовательно, , т.е. зависимые случайные величины Х и Y некоррелированы.

Таким образом, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не следует коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще не следует независимости этих величин. Однако, из некоррелированности нормально распределенных величин вытекает их независимость.

Вопрос 41. Нормальное распределение на плоскости.

Достаточно часто встречаются на практике двумерные случайные величины, распределение которых нормально. Нормальным законом распределения на плоскости называют распределение вероятностей двумерной случайной величины (Х,У), если

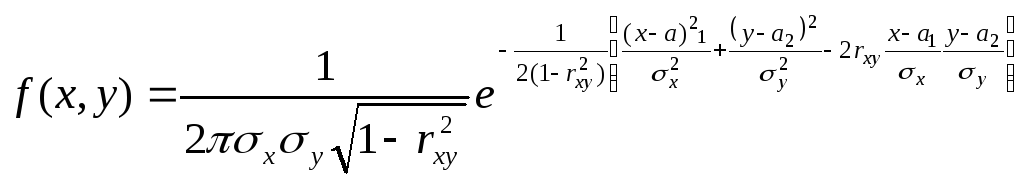(1). Нормальный закон на плоскости определяется пятью параметрами: а₁, а₂ (математические ожидания), (средние квадратические отклонения), r_xy (коэффициент корреляции величин X, Y). Убедимся в том, что если составляющие двумерной нормально распределенной случайной величины некоррелированны, то они и независимы. Пусть Х и Y некоррелированы. Тогда, полагая в формуле (1) r_xy=0, получаем

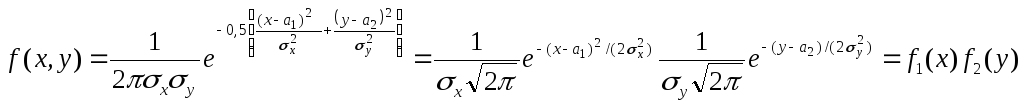
Таким образом, если составляющие нормально распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих, а отсюда следует независимость составляющих. Справедливо и обратное утверждение. Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.