Вопрос 1. Случайное событие. Классическое определение вероятности. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Предметом ТВ является изучение вероятностных закономерностей случайных событий. Классическое определение вероятности. Пример. В ящике находятся шары 1-δ, 6-τ. ω – элементарное событие. ω₁*ω₂* ω₇. Все возможные исходы испытания называются элементарными исходами. Всего исходов 7. А – событие, заключающееся, в том, что вынутый шар черный, тогда вероятность этого события Р(А). Р(А)=6/7. Р(В)=1/7 – белый шар. Вероятность появления события А Р(А)=m/n (1), равна отношению (1), где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. Перестановки – это комбинации из n элементов, в которых учитывается порядок их следования. Разделяют перестановки с повторениями и без повторений P_n=n!. Размещения из n по m элементов – это выборка m-элементов из n-элементного множества, в которой важен порядок следования элементов. Разделяют размещения с повторением и без повторений . Сочетания – это выборка m-элементов из n-элементного множества, в котором порядок не важен. Различают сочетания без повторений (это количество способов выбрать m-элементов из n-элементного множества) и с повторениями . Пусть некоторый элемент вида А может быть выбран n способами, а элемент В – m способами, тогда сложная выборка А и В осуществляется n*m – способами (тогда сложная выборка А или В осуществляется n+m – способами). События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. Все возможные исходы испытания несовместные между собой образуют полную группу событий. Если в полной группе всего два события, то события В называется противоположным А и наоборот. . Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) . Пример. 40 вопр., k=40, l=10 – которые выучил. В билете из 40 по 2. Экзамен сдан если студент ответит на два вопроса из билета. Найти вероятность того, что студент сдаст экзамен. А – событие, что студент сдаст. Р(А)=m/n, где n – общее количество способов составить билеты из 40 по 2. .

Вопрос 2. Относительная частота. Геометрическая вероятность. Вероятность появления события А. Р(А)=m/n (1), равна отношению (1), где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) . Пусть некоторое испытание произведено n-раз, причем в них событие А произошло m-раз, тогда относительной частотой появления события А называется отношение . Свойства относительной частоты: . Пример: n=40, m=22. . Геометрическая вероятность. Наугад ставится точка на этот отрезок. Найти вероятность, что она попадет на отрезок от z до ω. Т.к. место расположения маленького отрезка внутри большого не имеет значения, то Р=l/L. . Пример: Во внутрь круга с радиусом R бросается точка. Найти вероятность, что точка попала в кольцо между окружностями. .

Вопрос 3. Теорема сложения вероятностей несовместных событий. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. Все возможные исходы испытания несовместные между собой образуют полную группу событий. Если в полной группе всего два события, то события В называется противоположным А и наоборот. . Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) . Суммой двух событий А и В называют событие, заключающееся в появлении хотя бы одного из событий. Теорема: Вероятность суммы несовместных событий равна сумме вероятностей соответствующих событий: Р(А+В)=Р(А)+Р(В) (1). Доказательство: n – всего исходов, m₁ – благоприятные исходы для А, m₂ – благоприятные исходы для В. А+В= m₁ + m₂. Р(А+В)=m₁/n+m₂/n=(m₁+m₂)/n. Пример: Подбрасывается кубик. Найти вероятность того, что выпадет нечетное число. А₁ – 1, А₂ – 2, А₆=6. Р(А)=1/6., где i от 1 до 6. А – события выпадения нечетного числа. А= А₁ + А₃ + А₅. Р(А)= Р(А₁)+Р(А₃)+Р(А₅)=1/2. Следствие: вероятность равна сумме событий. Р(А₁+А₂+…+А_n)=Р(А₁)+Р(А₂)+…+Р(А_n).

Вопрос 4. Полная группа событий. Противоположные события. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. Все возможные исходы испытания несовместные между собой образуют полную группу событий. Если в полной группе всего два события, то события В называется противоположным А и наоборот. . Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) . Теорема 1: Пусть событие А₁…А_n образуют полную группу, тогда Р(А₁)+Р(А₂)+…+Р(А_n)= Р(А₁+А₂+…+А_n)=1, где А= А₁+А₂+…+А_n, т.к. события образуют полную группу, то событие А является достоверным. Теорема 2: . Воспользуемся теоремой 1.

Вопрос 5. Теорема сложения вероятностей совместных событий. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. Все возможные исходы испытания несовместные между собой образуют полную группу событий. Если в полной группе всего два события, то события В называется противоположным А и наоборот. . Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) . События А и В называются независимыми, если их вероятности не зависят от того произошло событие А или В. Совместные события, которые не исключают друг друга. Теорема: Пусть А и В – совместные, тогда Р(А+В)=Р(А)+Р(В)-Р(ВА). В случае если А и В независимые, то Р(АВ)=В(ВА)=Р(А)Р(В). Если А и В зависимы, то Р(АВ)=В(ВА)=Р(А)Р(В/А). Доказательство: В чем заключается появление А+В. ( по теореме о сложении несовместных событий: Вероятность суммы несовместных событий равна сумме вероятностей соответствующих событий: Р(А+В)=Р(А)+Р(В)), тогда (1), , (2). , (3). (3) и (2) в (1), получаем Р(А+В)=Р(А)-Р(АВ)+Р(В)-Р(АВ)+Р(АВ)=Р(А)+Р(В)-Р(АВ). Пример: Два стрелка стреляю р₁=0,8, р₂=0,9 – вероятности попадания. Найти вероятность того, что попадет хотя бы один. А – попал первый, В – попал второй. События совместны. 1 способ. Р(А+В)=Р(А)+Р(В)-Р(АВ)=0,8+0,9-0,8*0,9=0,98. 2 способ: , =0,8*0,1+0,2*0,9+0,8*0,9=0.98.

Вопрос 6. Формула полной вероятности. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А.. Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) . События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. Все возможные исходы испытания несовместные между собой образуют полную группу событий. Если в полной группе всего два события, то события В называется противоположным А и наоборот. .

Предполагается, что А может произойти только если произошло одно из следующих событий Н₁, Н₂,…, Н_n, образующих полную группу. События Н₁, Н₂,…, Н_n будем называть гипотезами. Найдем Р(А) в этих предположениях. А=Н₁А+Н₂А+…+Н_nА. События Н₁А,Н₂А,…,Н_nА зависимые. Р(А)= Р(Н₁А)+Р(Н₂А)+…+Р(Н_nА)=Р(Н₁)Р(А)+Р(Н₂)Р(А)+…+Р(Н_n)Р(А)=. - (1) – формула полной вероятности. Пример: В 1-м ящике 3 белых и 5 черных, во 2-м ящике – 4 белых и 7 черных. Из 2-го достают 1 шар. Найти Р, что вынутый шар черный. А – черный шар, Н₁ – из 1-го белый, Н₂ – из 1го черный. Р(А)=Р(Н₁)Р(А/Н₁)+Р(Н₂)Р(А/Н₂)=61/96,Р(Н₁)=3/8,Р(Н₂)=5/8,Р(А/Н₁)=7/12, Р(А/Н₂)=8/12=2/3.

Вопрос 7. Вероятность гипотез. Формула Байеса. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. Все возможные исходы испытания несовместные между собой образуют полную группу событий. Если в полной группе всего два события, то события В называется противоположным А и наоборот. . Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) .

Пусть А может осуществиться при выполнении одной из гипотез Н₁,Н₂,…,Н_n. Предполагается, что событие А уже произошло, определим как изменились вероятности гипотез в предположении, что произошло событие А. Р(Н₁А),Р(Н₂А),…,Р(Н_nА). . Р(А)=Р(Н₁)Р(А/Н₁)+…+Р(Н_n)Р(А/ Н_n). 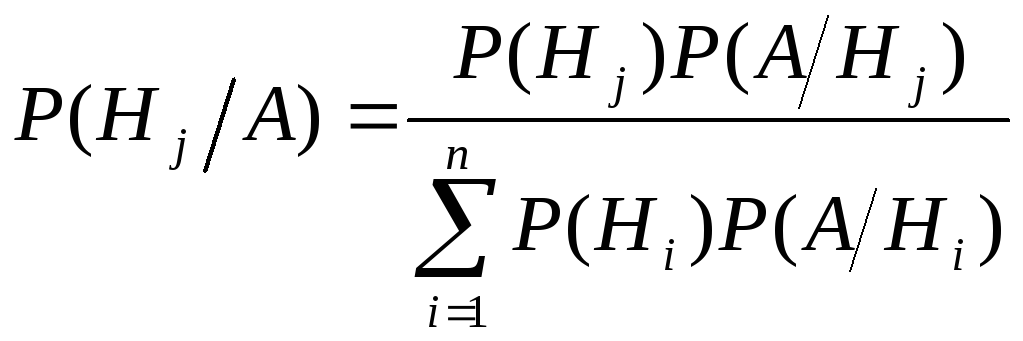- формула Байеса. Пример: В магазин привезли телевизоры 2-х фирм. Sony – 30%, Panasonic – 70%. Вероятность, что в течении гарантийного срока выйдет из строя р₁=0,1, р₂=0,2. 1) найти вероятность того, что покупатель купил телевизор Sony (при условии что он сломался); 2) Определить фирму, марка которой невероятнее всего был приобретен телевизор. А – сломался, Н₁ – был куплен Sony, H₂ – был куплен Panasonic. 1) . Р(А)=0,3*0,1+0,7*0,2=0,17. 2) .

Вопрос 8. Условная вероятность. Теорема умножения вероятностей. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. События А и В называются независимыми, если их вероятности не зависят от того произошло событие А или В. Произведением А и В называется событие, заключающееся в одновременном выполнении событий. Тогда вероятность того, что произошло В при условии, что выполнилось А, определим как (1). Теорема 1 (умножение вероятностей): Если события А и В зависимы, то Р(А*В)=Р(А)*Р(В/А) (2). Теорема 2: Пусть А и В независимы, то Р(А*В)=Р(А)*Р(В), т.к. условная вероятность совпадает с событием В. Пример: Два стрелка стреляют по мишеням. р₁=0,5, р₂=0,7. Найти вероятность, того 1) что попадет хотя бы один; 2) что попадут оба; 3) что не попадет ни один. 1) А – р₁, В – р₂, С – хотя бы один попал. С=С₁+С₂+С₃. т.к. висимы, то зависсимыпроизошло событие В при условии, что выполнилось А00000000000000000000000000000000000000000000000000 С₁ – попал 1, тогда , С₂ – попал 2, тогда , С₃ – попали оба, тогда . Р(С)= Р(С₁)+Р(С₂)+Р(С₃). Р(С)=0,5*0,3+0,5*0,7+0,5*0,7=0,85. 2) р(С)=0,35. 3) =0,15.

Вопрос 9. Независимые события. Теорема умножения для независимых событий. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. События А и В называются независимыми, если их вероятности не зависят от того произошло событие А или В. Произведением А и В называется событие, заключающееся в одновременном выполнении событий. Тогда вероятность того, что произошло В при условии, что выполнилось А, определим как (1). Теорема 1 (умножение вероятностей): Если события А и В зависимы, то Р(А*В)=Р(А)*Р(В/А) (2). Теорема 2: Пусть А и В независимы, то Р(А*В)=Р(А)*Р(В), т.к. условная вероятность совпадает с событием В. Пример: Два стрелка стреляют по мишеням. р₁=0,5, р₂=0,7. Найти вероятность, того 1) что попадет хотя бы один; 2) что попадут оба; 3) что не попадет ни один. 1) А – р₁, В – р₂, С – хотя бы один попал. С=С₁+С₂+С₃. т.к. висимы, то зависсимыпроизошло событие В при условии, что выполнилось А00000000000000000000000000000000000000000000000000 С₁ – попал 1, тогда , С₂ – попал 2, тогда , С₃ – попали оба, тогда . Р(С)= Р(С₁)+Р(С₂)+Р(С₃). Р(С)=0,5*0,3+0,5*0,7+0,5*0,7=0,85. 2) р(С)=0,35. 3) =0,15.

Вопрос 10. Формула Бернули. Достоверным называется событие, которое должно заведомо произойти при ряде условий. Невозможное событие – это событие, которое заведомо произойти не сможет. Под случайным событием понимают событие, которое может произойти или не может произойти. Предметом ТВ является изучение вероятностных закономерностей случайных событий. Вероятность появления события А. Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. События А и В называются несовместными, если произойти одновременно они не могут. События, которые могут произойти одновременно, называются совместными. Все возможные исходы испытания несовместные между собой образуют полную группу событий. Если в полной группе всего два события, то события В называется противоположным А и наоборот. . Свойства вероятности: 1) А – достоверное событие Р(А)=1; 2) В – невозможное событие Р(В)=0; 3) . События А и В называются независимыми, если их вероятности не зависят от того произошло событие А или В.

Предполагается, что производится n независимых испытаний, в каждом из которых некоторое событие А может появиться, а может и не появиться. Будем предполагать, что вероятность появления события А в каждом из испытаний одинаковая и равна р. Поставим задачу определить вероятность того, что в n испытаниях событие А произойдет ровно k раз. P_n(k), q=1-p – событие А не произойдет. Предположим: n=3, появится 1 раз. . Указанное событие сложное и заключается в том, что в n испытаниях событие А произойдет k раз и не произойдет (n-k) раз. . Пусть событие В заключается в том, что в n испытаниях А появится k-раз. В зависимости от того, в каком порядке событие А будет происходить или не происходить, можно выделить всего различных случаев. В каждом из таких случаев событие А происходит n-раз и не происходит n-k – раз. . . (используем теорему сложения несовместных событий: Вероятность суммы несовместных событий равна сумме вероятностей соответствующих событий: Р(А+В)=Р(А)+Р(В) и теорему об умножении независимых событий: Пусть А и В независимы, то Р(А*В)=Р(А)*Р(В)). Формула оценки для наивероятнейшего числа наступлений события А в n-испытаниях. (k₀ – наивероятнейшее число). .

Вопрос 11. Локальная и интегральная теоремы Муавра-Лапласа. Локальная теорема. В связи с тем, что формула Бернулли применима при достаточно небольших n и k, будем рассматривать асимптотическую (n→∞) вероятность появления в n – независимых испытаниях некоторого события А k-раз. Вероятность появления равна р (). Теорема: если вероятность р появления события А в каждом из испытаний отлично от 0 и 1, тогда вероятность того, что событие А в n испытаниях произойдет k раз. , , , . При . Пользуемся таблицей приложения 1. Интегральная теорема. Найдем вероятность того, что в n испытаниях событие А произойдет не менее чем k₁ и не более чем k₂ раз. , n велико. Р отлично от 0 и 1. Теорема: Вероятность того, что в n-независимых испытаниях событие А происходит от k₁ до k₂ раз. , где , - функция Лапласа, Ф(-х)=-Ф(х) – нечетная, , . Когда x>5, то Ф(х)=0,5; (По Колде:Ф(-∞)=0, Ф(∞)=1 и Ф(0)=0,5). Пользуемся таблицей приложения 2. Замечание: т.к. , тогда . .

Вопрос 12. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях. Вероятность появления события А Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. Локальная теорема Муавра-Лапласа: если вероятность р появления события А в каждом из испытаний отлично от 0 и 1, тогда вероятность того, что событие А в n испытаниях произойдет k раз. . Интегральная теорема Муавра-Лапласа: Вероятность того, что в n-независимых испытаниях событие А происходит от k₁ до k₂ раз. . Найдем вероятность того, что относительная частота появления события А k/n отклонится от вероятности р, по абсолютной величине не более чем ε. , . , делаем .. .

Вопрос 13. Дискретная и непрерывная СВ. Закон распределения дискретной СВ. Биномиальное распределение. Вероятность появления события А Р(А)=m/n, равна отношению, где n – общее число исходов испытания; m – число элементарных исходов, благоприятствующих появлению события А. Если в результате некоторого испытания появляется величина, которая может принимать одно из вполне определенных значений, то такая величина называется случайной. Случайные величины: 1) дискретные (конечное или бесконечное число отдельных дискретных значений); 2) непрерывные (любое значение как правило из интервала.).

Для того чтобы определить закон распределения вероятности ДСВ достаточно перечислить все возможные значения и указать соответствующие вероятности, с которыми СВ принимает то или иное значение. Х,У – СВ, х,у – значения. Х=х₁+х₂+х_n. Р=р₁+р₂+…+р_n=1. (бесконечный ряд сходится и его сумма равна 1). Существует и геометрический способ задания: (многоугольник распределения), по оси Х – возможные значения СВ, а по У – соответствующие вероятности.

Биномиальное распределение. Производится n независимых испытаний, вероятность появления А равна р. В качестве Х – СВ будем рассматривать появление А в испытании. Х=1,2,…,n. . . Т.к. вероятность соответствует коэффициентам бинома Ньютона, тогда получим: .

Вопрос 14. Распределение Пуассона. Простейший поток событий. Производится n независимых испытаний (n велико), в каждом испытании вероятность появления А равна р, где р мало (p<0,1). В этих условиях для нахождения вероятности появления события А ровно k-раз нельзя воспользоваться локальной теоремой Муавра-Лапласа (Локальная теорема Муавра-Лапласа: если вероятность р появления события А в каждом из испытаний отлично от 0 и 1, тогда вероятность того, что событие А в n испытаниях произойдет k раз. ). , предполагаем, что значение остается постоянным, т.е. чем > n→∞, тем > р→0. (это означает, что среднее количество появления события А при разном числе испытаний остается постоянным). .

, где

, , где , .

(1) - закон Пуассона (n – большое, р<0,1).

Простейший поток событий. Потоком событий называют последовательность событий, которые могут наступить в случайный момент времени (прибытие автобуса, прибытие клиентов). Свойства: 1) Свойство стационарности. Заключается в том, что вероятность того, что за промежуток времени длительности t произойдет ровно k-событий, независящих от начала отсчета промежутка времени, а зависит от k и длины этого промежутка. 2) Отсутствие поля действия. Вероятность того, что за t появится ровно k событий не зависит от того появилось ли это событие в предшествующие этому промежутку моменты времени. 3) Ординарность. Заключается в том, что вероятность происхождения двух или более событий в бесконечно малый промежуток времени t ничтожно мала по сравнению с вероятностью происхождения одного события.

Поток событий, обладающий свойствами 1, 2, 3 называется простейшим потоком событий. На практике, если поток событий складывается из большого количества независимых друг от друга стационарных потоков, то он является простейшим потом событий. Предположим, что потом простейший. λ – интенсивность потока, т.е. среднее значение появления события в единицу времени. (2). Формула зависит только от k и t, значит свойство стационарности выполняется. Свойство Отсутствие поля действия тоже выполняется. Предположим, что t→∞. , , где (ряд), , , т.к. t→0, то вероятность того, что произойдет события во много меньше, чем вероятность одного события .

Вопрос 15. Геометрическое и гипергеометрическое распределения.

Геометрическое распределение.

Производится неограниченное количество испытаний до тех пор пока не произойдёт событие

p – постоянна

1-p – вероятность непоявления события

X – количество проведенных испытаний

X = 1,2,3…

X	1	2	3	4	…	k	…
p	p	qp	q2p	q3p		qk-1p

бесконечно убывающая геометрическая прогрессия

Случайная величина, распределённая по этому закону называется геометрическим распределением.

_____________________

Пример:

5 выстрелов

p=0,8 n=5

составим закон распределения случайной величины, равной произведению выстрелов

X	1	2	3	4	5
p	0,8	0,2∙0,8	0,22∙0,8	0,23∙0,8	0,24∙0,8

______________________

Гипергеометрическое распределение.

N - всего изделий M – бракованные изделия

K - выбирается

Определить вероятность что из них l окажется бракованных.

Всего возможных способов выбрать K из N:

Случайная величина распределенная по этому закону называется гипергеометрическим распределением.

Вопрос 16. Математическое ожидание дискретной случайной величины и его свойства.

Математическое ожидание. Его свойства.

X	X1	X2	…	Xn
p	p1	p2	…	pn

Математическим ожиданием дискретной случайной величины называется сумма произведений ее значений на соответствующие вероятности.

Пример:

Найти математическое ожидание числа появлений событий A в одном испытании если вероятность этого события в каждом из испытаний равна p.

X – число появления событий A в одном испытании.

X	0	1
p	1-p	p

Математическое ожидание числа появления события в 1ом испытании равно вероятности этого события.

Св-ва математического ожидания:

X	C
p	1

1)

2)

Произведение случайной величины на число C

под произведением понимается случайная величина , которая может принимать все возможные значения случайной величины , умноженной на константу .

X	X1	X2	…	Xn
p	p1	p2	…	pn

СX	СX1	СX2	…	СXn
p	p1	p2	…	pn

3) Определ. произведение случайных величин

если	Xзнач	X1	X2
а	Yзнач	Y1	Y2

Независимые случайные величины – если соответствующая вероятность одной случайной величины не зависит от того какое значение приняла другая случайная величина.

Если случайные величины независимы, то математическое ожидание их произведения равно произведению их математических ожиданий.

Y	y1	y2
p	q1	q2

4) Случайные величины X и Y определяют сумму случайных величин как некоторую величину , которая может принимать все возможные значения сумм.

Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий. Справедливо как для зависимых так и независимых величин.

X	x1	x2
p	p1	p2

X+Y	x1+y1	x1+y2	x2+y1	x2+y2
p	p11	p12	p21	p22

Y	y1	y2
p	q1	q2

Вероятности могут принимать различные значения, в зависимости от того будут случайные величины зависимыми или независимыми.

- В случае независимых случайных величин соответствующие вероятности перемножаются.

- В случае зависимых случайных величин вероятность того, что случайная величина приняла значение умножаем на соответствующую условную вероятность того что приняла значение .

Рассмотрим в отдельности каждую скобку

; ; ;