
- •Вопрос 15. Геометрическое и гипергеометрическое распределения.
- •Вопрос 16. Математическое ожидание дискретной случайной величины и его свойства.
- •Вопрос 17. Вероятностный смысл мат. Ожидания. Математическое ожидание числа появлений события в независимых испытаниях.
- •Вопрос 18. Дисперсия дискретной случайной величины и ее свойства. Введем случайную величину представляющую собой отклонение от математического ожидания.
- •Вопрос 19. Дисперсия числа появления событий в независимых испытаниях. Среднее квадратическое отклонение.
- •Вопрос 20. Мат. Ожидание, дисперсия и среднее квадратическое отклонение среднего арифметического одинаково распределенных взаимно независимых величин.
- •Вопрос 21. Неравенство Чебышева.
- •Вопрос 22. Теорема Чебышева.
- •Вопрос 23. Теорема Бернулли.
- •Вопрос 24. Функция распределения и ее свойства.
- •Вопрос 25. Плотность распределения, ее свойства.
- •Вопрос 26. Вероятность попадания случайной величины в заданный интервал. Нахождение функции распределения по известной плотности распределения. Вероятностный смысл плотности распределения.
- •Вопрос 27. Числовые характеристики непрерывной случайной величины. Числовые характеристики св
- •Математическое ожидание (мо)
- •Мо основных св
- •Дисперсия св
- •Дисперсия основных св
- •Математическое ожидание и дисперсия суммы случайных величин
- •Вопрос 28. Закон равномерного распределения.
- •Вопрос 29. Нормальное распределение
- •Вопрос 30. Нормальная кривая (Кривая Гаусса).
- •Вопрос 31. Вероятность попадания нормально распределенной случайной величины в интервал.
- •Вопрос 32. Вероятность отклонения нормально распределенной случай ной величины.
- •Вопрос 33. Показательное распределение
- •Вопрос 34. Функция надежности
- •Вопрос 35. Закон распределения вероятностей двумерной случайной величины.
- •Вопрос 36. Вероятность попадания случайной величины в полуполосу.
- •Вопрос 37. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины.
- •Вопрос 38. Нахождение плотностей вероятности составляющих двумерной случайной величины.
- •Вопрос 39. Зависимые и независимые случайные величины. Корреляционный момент и коэффициент корреляции.
- •Вопрос 40. Коррелированность и зависимость случайных величин.
- •Вопрос 41. Нормальное распределение на плоскости.
- •Вопрос 42. Линейная регрессия. Прямые линии среднеквадратической регрессии.
- •Вопрос 43. Характеристическая функция случайной величины. Основные свойства. Формула обращения и теорема единственности.
- •Вопрос 44. Цепи Маркова. Вероятность перехода за n шагов. Эргодическая теорема Маркова.
- •Вопрос 45. Марковские процессы. Процессы гибели и размножения
- •Вопрос 46. Стационарный случайный процесс. Теорема Хинчина.
- •Вопрос 47. Понятие стохастического интеграла. Теорема о спектральном представлении.
- •Вопрос 48. Задачи математической статистики. Выборка. Статистический и вариационный ряды.
- •Вопрос 49. Полигон и гистограмма. Эмпирическая функция распределения.
- •Вопрос 50. Понятие оценки параметров распределения. Оценка генеральной средней по выборочной средней.
- •Вопрос 51. Генеральная и выборочная дисперсия. Вычисление дисперсии.
- •Вопрос 52. Оценка генеральной дисперсии по исправленной выборочной.
- •Вопрос 53. Доверительные интервалы для оценки математического ожидания нормального распределения при известном .
- •Вопрос 54. Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном .
- •Вопрос 55. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения.
- •Вопрос 56. Оценка вероятности биномиального распределения по относительной частоте.
- •Вопрос 57. Выборочные уравнения регрессии.
- •Вопрос 58. Выборочный коэффициент корреляции.
- •Вопрос 59. Понятие статистической гипотезы. Статистический критерий проверки нулевой гипотезы
- •Вопрос 60. Критическая область. Отыскание критической области.
- •Вопрос 61. Сравнение двух дисперсий нормальных генеральных совокупностей.
- •Вопрос 62. Проверка гипотезы о нормальном распределении. Критерий согласия Пирсона.
Вопрос 36. Вероятность попадания случайной величины в полуполосу.
 Y
Y




 Y1
(x1,y1)
(x2,y1)
P(x1<X<x2
, Y<y1)
= F(x2
, y1)
- F(x1
, y1)
Y1
(x1,y1)
(x2,y1)
P(x1<X<x2
, Y<y1)
= F(x2
, y1)
- F(x1
, y1)















 y
y





 y2
(x1,y2)
y2
(x1,y2)













 (x1,y1)
(x1,y1)


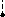 X1
X2
X y1
X1
X2
X y1
X
X1
P(X<x1 , y1<Y<y2) = F(x1 , y1) - F(x1 , y1)














 Y2
(x1,y2)
(x2,y2)
P(x1<X<x2
, y1<Y<y2)
= F(x2
, y2)
- F(x1
, y2)
– [F(x2
, y1)
- F(x1
, y1)]
=
Y2
(x1,y2)
(x2,y2)
P(x1<X<x2
, y1<Y<y2)
= F(x2
, y2)
- F(x1
, y2)
– [F(x2
, y1)
- F(x1
, y1)]
=
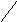
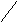
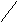
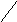



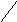
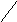
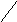
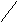

 = F(x1
, y1)
+ F(x2
, y2)
- F(x1
, y2)
- F(x2
, y1)
(*)
= F(x1
, y1)
+ F(x2
, y2)
- F(x1
, y2)
- F(x2
, y1)
(*)


 Y1 (x1,y1)
(x2,y1)
Y1 (x1,y1)
(x2,y1)

X1 X2
Вопрос 37. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины.
Определение: Вторая смешанная частная производная от функции распределения.
![]() (1) Вероятностный смысл совместной
плотности распределения.
(1) Вероятностный смысл совместной
плотности распределения.
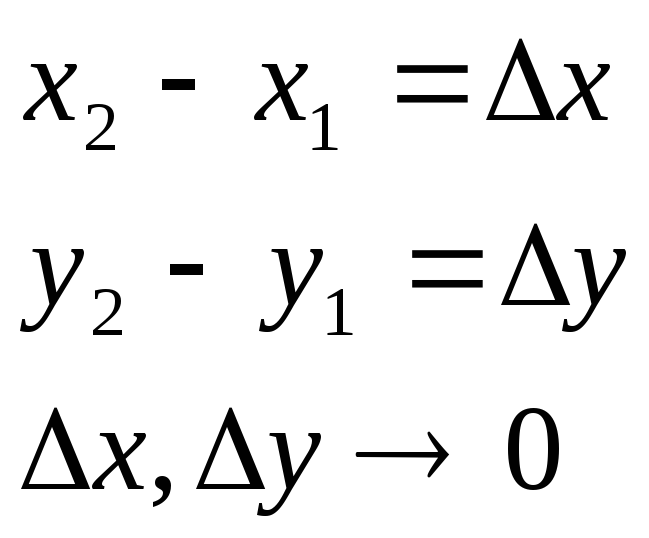
PABCD = [F(x2 , y2) - F(x1 , y2)] – [F(x2 , y1) - F(x1 , y1)] =
PABCD – вероятность попадания в плоскость. Воспользуемся формулой (1)
![]()
=
![]()
![]() (2)
(2)
Вероятностный смысл (2) – плотность распределения представляет собой:
![]()
D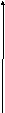




















 Y
Y
![]()
X
Тогда по формуле (2) Р попадания в каждый мелкий квадратик
![]()
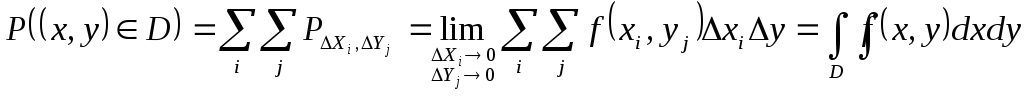
![]() (3)
(3)
Нахождение функции распределения по известной плотности.
![]()
![]()
![]()
![]()
Свойства:
-
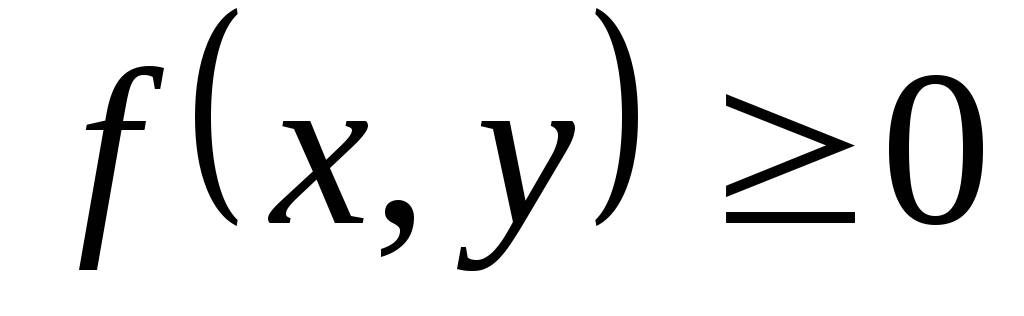 Доказательство основано на вероятностном
смысле плотности распределения.
Доказательство основано на вероятностном
смысле плотности распределения.
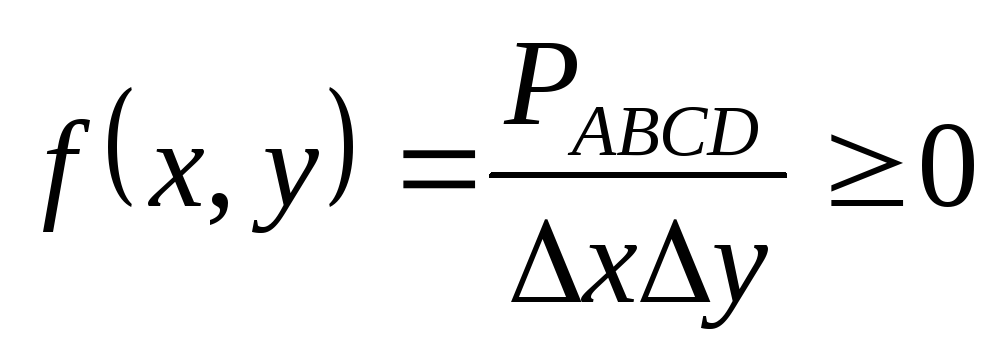
-
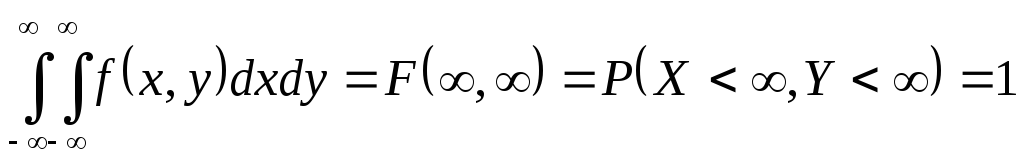
Вопрос 38. Нахождение плотностей вероятности составляющих двумерной случайной величины.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
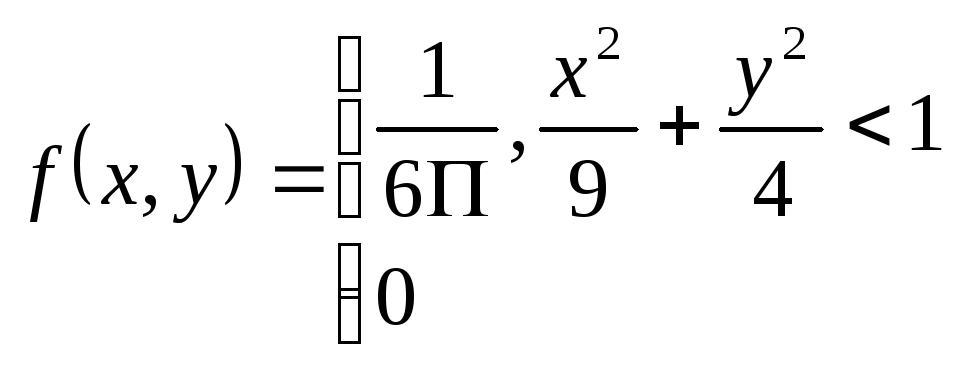

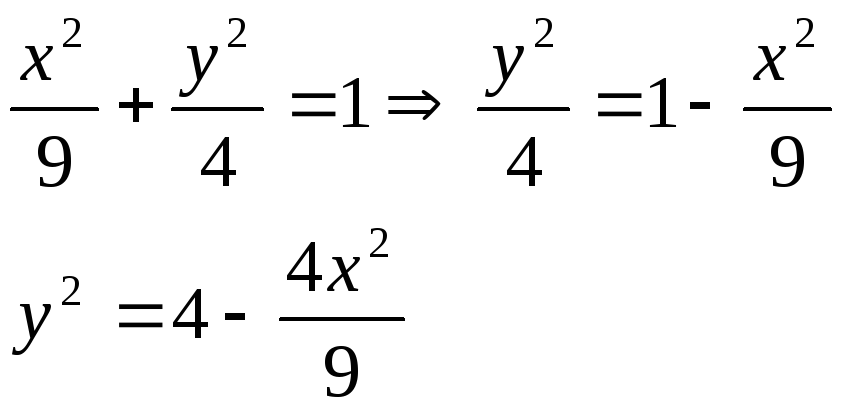
![]()
Вопрос 39. Зависимые и независимые случайные величины. Корреляционный момент и коэффициент корреляции.
Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Отсюда следует, что условные распределения независимых величин равны их безусловным распределениям.
Необходимые и достаточные условия независимости случайных величин.
Теорема: Для того, чтобы случайные величины Х, Y были независимыми, необходимо и достаточно, чтобы функция распределения системы (Х, Y) была равна произведению функций распределения составляющих: F(x,y)=F1(x) F2(y)
Доказательство: а) Необходимость. Пусть Х и Y независимы. Тогда события X<x и Y<y независимы, следовательно, вероятность совмещения этих событий равна произведению их вероятностей:
P(X<x , Y<y) =P(X<x ) P(Y<y) или F(x,y)=F1(x) F2(y).
б) Достаточность. Пусть F(x,y)=F1(x) F2(y). Отсюда P(X<x , Y<y) =P(X<x ) P(Y<y), т.е. вероятность совмещения событий X<x и Y<y равна произведению вероятностей этих событий. Следовательно, случайные величины X и Y независимы.
Следствие: Для того чтобы непрерывные
случайные величины Х и Y
были независимыми, необходимо и
достаточно, чтобы плотность совместного
распределения системы (Х,Y)
была равна произведению плотностей
распределения составляющих: f(x,y)=f1(x)
f2(y).
Доказательство: а) Необходимость.
Пусть Х и Y - независимые
непрерывные случайные величины. Тогда
(на основании предыдущей теоремы):
F(x,y)=F1(x)
F2(y).
Дифференцируя это равенство по х, а
потом по y, имеем:
![]() ,
или (по определению плотностей
распределения двумерной и одномерной
величин) f(x,y)=f1(x)
f2(y).
,
или (по определению плотностей
распределения двумерной и одномерной
величин) f(x,y)=f1(x)
f2(y).
б) Достаточность. Пусть f(x,y)=f1(x) f2(y). Интегрируя это равенство по х, а потом по y, получим:
![]() или F(x,y)=F1(x)
F2(y).
Следовательно, Х и Y
независимы.
или F(x,y)=F1(x)
F2(y).
Следовательно, Х и Y
независимы.
Для описания системы двух случайных
величин кроме математических ожиданий
и дисперсий составляющих используют и
другие характеристики: корреляционный
момент и коэффициент корреляции.
Корреляционным моментом
![]() случайных величин Х и Y
называют математическое ожидание
произведения отклонений этих величин:
случайных величин Х и Y
называют математическое ожидание
произведения отклонений этих величин:
![]() Для
вычисления корреляционного момента
дискретных величин используют формулу:
Для
вычисления корреляционного момента
дискретных величин используют формулу:
![]() ,
а для непрерывных величин – формулу:
,
а для непрерывных величин – формулу:
![]() .
Корреляционный момент служит для
характеристики связи между величинами
X и Y.
Корреляционный момент =0, если X
и Y независимы.
.
Корреляционный момент служит для
характеристики связи между величинами
X и Y.
Корреляционный момент =0, если X
и Y независимы.
Теорема: Корреляционный момент двух независимых случайных величин X и Y =0.
Доказательство: Т.к. Х и Y
– независимые случайные величины, то
их отклонения X-M(X)
и Y-M(Y)
также независимы. Пользуясь свойствами
математического ожидания (мат. ожидание
произведения независимых случайных
величин равно произведению математических
ожиданий сомножителей) и отклонения
(математическое ожидание отклонения
равно нулю), получаем:
![]()
![]() =0.
Из определения корреляц.момента следует,
что он имеет размерность , равную
произведению размерностей величин Х и
Y.
=0.
Из определения корреляц.момента следует,
что он имеет размерность , равную
произведению размерностей величин Х и
Y.
Коэффициент корреляции rxy
случайных величин Х иY
- это отношение корреляционного момента
к произведению средних квадратических
отклонений этих величин:
![]() .
Так как размерность момента корреляции
равна произведению размерностей величин
X и Y,
.
Так как размерность момента корреляции
равна произведению размерностей величин
X и Y,
![]() имеет размерность величины X,
а
имеет размерность величины X,
а
![]() - размерность величины Y,
то rxy
– безразмерная величина. Таким
образом, величина коэффициента корреляции
не зависит от выбора единиц измерения
случайных величин. В этом преимущество
коэффициента корреляции перед
корреляционным моментом.
- размерность величины Y,
то rxy
– безразмерная величина. Таким
образом, величина коэффициента корреляции
не зависит от выбора единиц измерения
случайных величин. В этом преимущество
коэффициента корреляции перед
корреляционным моментом.
Теорема: Абсолютная величина
корреляционного момента двух случайных
величин Х и Y не превышает
среднего геометрического их дисперсий:![]() .
Доказательство: Введем в рассмотрение
случайную величину
.
Доказательство: Введем в рассмотрение
случайную величину
![]() и найдем ее дисперсию D(Z1)=
и найдем ее дисперсию D(Z1)=![]() .
Выполнив выкладки, получим
.
Выполнив выкладки, получим
![]() .
Любая дисперсия неотрицательна, поэтому
.
Любая дисперсия неотрицательна, поэтому
![]() .
Отсюда
.
Отсюда
![]() (1). Введя случайную величину
(1). Введя случайную величину
![]()
![]() ,
аналогично найдем
,
аналогично найдем
![]() (2). Теперь объединим (1) и(2):
(2). Теперь объединим (1) и(2):
![]() (3) или
(3) или
![]() .
И таким образом,
.
И таким образом,
![]() .
.
Теорема: Абсолютная величина
коэффициента корреляции не превышает
единицы:
![]() .
.
Доказательство: Разделим обе части двойного неравенства (3) на произведение положительных чисел
![]() :
-1
:
-1![]() .
Итак,
.
Итак,
![]() .
.
