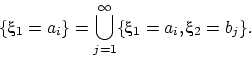23)Определение вероятности

Поставим каждому элементарному исходу  в соответствие число  так, что

Назовём число  вероятностью элементарного исхода . Вероятностью события  назовём число

равное сумме вероятностей элементарных исходов, входящих в множество . В случае  положим .

24) Показательное распределение, его функции распределения и плотности.

 имеет показательное (экспоненциальное) распределение с параметром , и пишут: , если  имеет следующую плотность распределения:

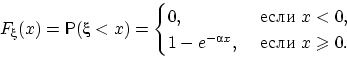
Ф-ция распределения случайной величины  непрерывна:

Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «нестарения» 

Пусть . Тогда для любых  :

25) Попарная независимость событий

Если события  независимы в совокупности, то они попарно независимы, т.е. любые два события  независимы.

26) Правило трёх сигм

Если , то 

27) Равномерное распределение на [a;b] и его функции распределения и плотности

Говорят, что  имеет равномерное распределение на отрезке , и пишут: , если плотность распределения  постоянна на отрезке  и равна нулю вне него:

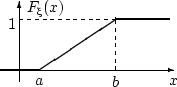
Очевидно, что площадь под графиком этой функции равна единице и . Поэтому   является плотностью распределения.

Случайная величина  имеет смысл координаты точки, выбранной наудачу на отрезке . Вычислим функцию распределения случайной величины :

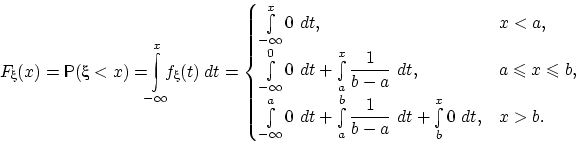
Получим следующую непрерывную функцию распределения:

 

28)Распределение Пуассона и его связь с биномиальным распределением

 Пусть  и  так, что . Тогда для любого  вероятность получить  успехов в  испытаниях схемы Бернулли с вероятностью успеха  стремится к величине :

Набор чисел   называется распределением Пуассона с параметром .

Пусть  — произвольное множество целых неотрицательных чисел,  — число успехов в  испытаниях схемы Бернулли с вероятностью успеха , . Тогда

29)Распределение Коши. В чём его особенность?

Говорят, что  имеет распределение Коши с параметрами , , и пишут: , если  имеет следующую плотность распределения:

Плотность распределения Коши симметрична относительно прямой  и похожа на плотность нормального распределения, но имеет более толстые «хвосты» на . Функция распределения случайной величины  с распределением Коши равна   при всех .

30) Распределения, возникающие как предел биномиального распред-ния

Говорят, что случайная величина  имеет биномиальное распределение с параметрами  и , и пишут: , если  принимает значения  с вероятностями Случайная величина с таким распределением имеет смысл числа успехов в  испытанияхсхемы Бернулли с вероятностью успеха . Таблица распределения  имеет вид:

31) Разложение в ряд Тейлора для характеристической функции

Пусть существует момент порядка  случайной величины , т.е. . Тогда характеристическая функция  в окрестности точки  разлагается в ряд Тейлора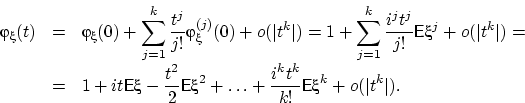

32) свойства вероятности

1. ;;

2.  Если  и  несовместны, то ;

3.  В общем случае ;

4.  Если , то .

33) Свойства математического ожидания и дисперсии

Математическое ожидание постоянной величины равно самой постоянной.

Постоянный множитель можно выносить за знак математического ожидания.

Дисперсия постоянной величины равна нулю.

Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

34) Свойства математического ожидания и дисперсии для независимых случайных величин

Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, справедливо для произвольного числа случайных величин.

Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых, справедливо для произвольного числа случайных величин.

Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

37) слабая сходимость случайных величин

 последовательность случайных величин  сходится слабо или по распределению к случайной величине  и пишут: , если для любого  такого, что функция распределения  непрерывна в точке , имеет место сходимость при .

слабая сходимость — это сходимость функций распределения во всех точках непрерывности предельной функции распределения.

38) Следствие из неравенства Чебышева

Если , то 

39) случайная величина

Функция   называется случайной величиной, если для любого борелевского множества  множество  является событием, т.е. принадлежит -алгебре .

Функция  называется случайной величиной, если для любых вещественных  множество  принадлежит -алгебре .

40) события независимые в совокупности

События  называются независимыми в совокупности, если для любого  и любого набора различных меж собой индексов  имеет место равенство:

41) Совместное и маргинальное распределение компонент случайного вектора

Функция  называется функцией распределения вектора  или функцией  совместного распределения случайных величин .

свойства функции совместного распределения:.

1) Для любых  верно неравенство: .

2) не убывает по каждой координате вектора .

3) Для любого  существует  . . Сущ. двойной предел .

4) Функция  по каждой координате вектора  непрерывна слева.

5) Чтобы по функции совместного распределения восстановить функции распределения  и  в отдельности, следует устремить мешающую переменную к :

Таблицы распределения каждой из случайных величин ,  в отдельности (таблицы частных, или маргинальных распределений) восстанавливаются по таблице совместного распределения с помощью формул:

Так, первое равенство следует из того, что набор , , ...   есть полная группа событий, и поэтому событие  раскладывается в объединение попарно несовместных событий: