17)Мат. Ожидание и дисперсия для непрерывных случайных величин

Пусть задано вероятностное пространство  и определённая на нём случайная величина X. То есть, по определению,  — измеримая функция. Если существует интеграл Лебега от X по пространству Ω, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается M[X] или .

Если F_X(x) — функция распределения случайной величины, то её математическое ожидание задаётся

Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью f_X(x), равно

18) Мода и медиана

Мода — значение во множестве наблюдений, которое встречается наиболее часто. Случайная величина может не иметь моды. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.Мода, как средняя величина, употребляется чаще для данных, имеющих нечисловую природу.. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.

Медиа́на — возможное значение признака, которое делит ранжированную совокупность на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана. Медиана является важной характеристикой распределения случайной величины и может быть использовано для центрирования распределения. Медиана определяется для широкого класса распределений, а в случае неопределённости, в то время как математическое ожидание может быть не определено.

19) Мультиномиальное распределение и его функция плотности

Пусть  — независимые одинаково распределённые случайные величины, такие, что их распределение задаётся функцией вероятности

Интуитивно событие {Xi = j} означает, что испытание с номером i привело к исходу j. Пусть случайная величина Yj равна количеству испытаний, приведших к исходу j:

Тогда распределение вектора имеет функцию вероятности

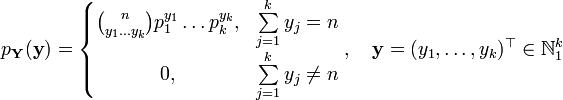
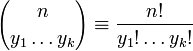
Мультин-ный коэффициент

,где

20) Независимость булевых алгебр

События  и  называются независимыми, если .

Пусть . Тогда события  и  независимы тогда и только тогда, когда . Если , то события  и  независимы тогда и только тогда, когда.

Пусть события  и  несовместны. Тогда независимыми они будут только в том случае, если  или 

Если события  и  независимы, то независимы и события  и ,  и ,  и .

21) Неравенство Чебышева

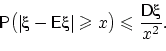
 Если , то для любого  :

22) Несовместные события

1. События  и  называют несовместными, если .

2. События  называют попарно несовместными, если для любых , где , события  и несовместны.

3. Говорят, что событие  влечёт событие , и пишут , если всегда, как только происходит событие , происходит и событие . На языке теории множеств это означает, что любой элементарный исход, входящий в множество , одновременно входит и в множество , т.е.  содержится в .