§ 11. Уравнение прямой линии на плоскости

1°. Векторное, параметрическое, общее и каноническое уравнение прямой в произвольной аффинной системе координат.

Фиксируем на плоскости аффинную систему координат, определяемую началом координат и базисными векторами . Тогда  точка плоскости определяется координатами .

Пусть прямая линия лежит в плоскости и проходит через точку параллельно вектору .

M

M₀

O

Рис.1. Прямая , проходящая через точку

параллельно вектору .

Определение 1. Всякий ненулевой вектор , параллельный прямой l, называется направляющим вектором этой прямой.

Если точка плоскости лежит на прямой, то вектор коллинеарен . Значим, R такое, что

.

(1)

С другой стороны, всякая точка М, для которой выполнено уравнение (1), принадлежит прямой в силу определения произведения вектора на число.

Таким образом, условие Мвыполнению уравнения (1). Уравнение (1) называется векторным уравнением прямой.

Если обозначить радиус вектора точек через и соответственно, то и уравнение (1) принимает вид:

,

(2)

которое также называется векторным уравнением прямой.

Если , то (2) в координатах принимает вид

(3)

– параметрическое уравнение прямой на плоскости, проходящей через точку в направлении вектора .

Исключая из уравнения (3) параметр t, получаем

(4)

– каноническое уравнение прямой на плоскости.

Уравнение (4) понимается как пропорцию. Тогда, если, например, , то прямая параллельна оси Oy и проходит через точку .

Приведем уравнение (4) к общему знаменателю:

.

Если обозначить , то получим:

(5)

– общее уравнение прямой на плоскости.

Так как , то хотя бы один из коэффициентов А или В отличен от нуля ⇒ уравнение (5) представляет собой уравнение первого порядка. Таком образом, показано, что любая прямая является алгебраической линией первого порядка.

Верно и обратное: любая алгебраическая линия первого порядка на плоскости является прямой.

Действительно, уравнение (5) является линейным неоднородным уравнением, и в силу теории решения СЛНУ его общее решение имеет вид

где – частное решение уравнения (5) (например, при , частного решения можно выбрать вида , ), – фундаментальное решение соответствующего однородного уравнения. Сравнивая общее решение уравнения (5) с (3), представляющим собой параметрическое уравнение прямой на плоскости, можно видеть, что множество всех решений уравнения (5) представляет собой прямую, проходящую через точку и имеющей направляющий вектор .

Таким образом доказана следующая теорема.

Теорема 1. Прямые на плоскости – алгебраические линии первого порядка.

Из доказательства теоремы 1 следует, что если – уравнение прямой, то вектор является направляющим вектором этой прямой.

Если , то из уравнения (5) получаем:

,

т.е.

, где .

Отметим, что в произвольной декартовой системе координат коэффициент не играет роль углового коэффициента (т.е. не равен тангенсу угла наклона прямой к оси ). Например, на рис. 2 прямая имеет уравнение (или в каноническом виде ) и перпендикулярна оси

L

y

l

x

Рис.2. Прямая в системе координат имеет уравнение .

Из канонического уравнения (4) легко выводится уравнение прямой, проходящей через 2 точки. А именно, если прямая l проходит через две точки и , то вектор можно выбрать в качестве направляющего вектора прямой. Тогда уравнение (4) принимает вид

,

(6)

который называется уравнением прямой, проходящей через точки и .

Рассмотрим некоторые частные случаи общего уравнения прямой (5)._.

1. Если А=0, то прямая параллельна оси .

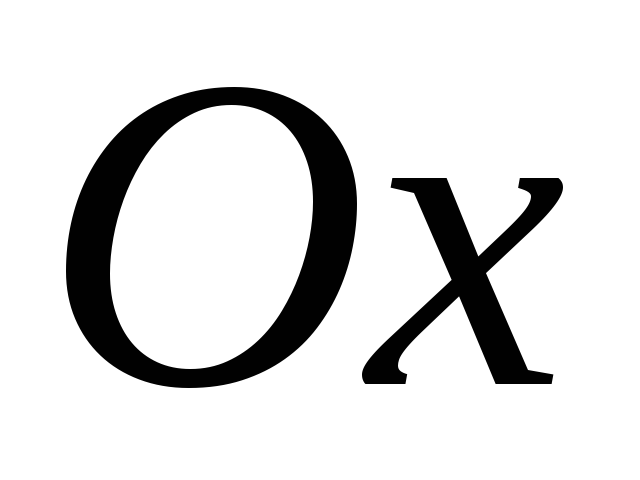2. Если B=0, то прямая параллельна оси .

3. Если C=0, то прямая проходит через начало координат.

4. Если A=C=0, то прямая совпадает с осью .

5. Если B=C=0 , то прямая совпадает с осью .

6. Если , то уравнение (5) после деления на можно переписать в виде

,

который называется уравнением прямой в отрезках. Здесь и равны отрезкам, отсекаемым прямой на координатных осях.

2°. Взаимное расположение прямых на плоскости. Полуплоскости.

Пусть на плоскости задана аффинная система координат .

Утверждение 1. Для того чтобы прямые и , задаваемые соответственно уравнениями

,

(7)

и

,

(8)

совпадали, необходимо и достаточно, чтобы

.

(9)

Доказательство.

| Если прямые l₁ и l₂ совпадают, то это означает, что их направляющие вектора и коллинеарные, т.е. R:

.

(10)

Пусть т. принадлежит этим прямым. Тогда

.

Умножая первое уравнение на и прибавляя ко второму, в силу (10) имеем , что вместе с (10) эквивалентно (9).

| Пусть выполняется (9). Тогда уравнения (7) и (8) эквивалентны  соответствующие прямые совпадают, ч.т.д.∎

Утверждение 2. Прямые и , задаваемые уравнениями (7) и (8) соответственно, параллельны и не совпадают 

.

(11)

Доказательство.

| Если прямые и параллельны и не совпадают, то система несовместна, а это эквивалентно (в силу теоремы Кронекера-Конелли) условию ,

Последнее равносильно условию , что возможно лишь при выполнении (11).

| Из первого равенства (11)  что прямые и параллельны, а из второго неравенства система уравнений (7), (8) несовместна  прямые параллельны и не совпадают, ч.т.д.∎

Следствие (из утверждений 1 и 2). Прямые и пересекаются 

.

(12)

Утверждение 3. Пусть прямые и , задаваемые уравнениями (7), (8), пересекаются в единственной точке . Тогда прямая l₃ проходит через точку  она задается уравнением

, ,

(13)

являющимся линейной комбинацией уравнений (7), (8).