18.Длина дуги
1. Длина дуги в прямоугольной системе координат
Пусть кривая L задана уравнением у = у(х),причем
у(х)
— непрерывно дифференцируемая функция
на [а, Ь]. Разобьем ее на п частей точками
с абсциссамии проведем хорды через эти
точки (рис. 18.9, а). Получим вписанную
ломаную, причем длинаеего звена равна
где
По теореме Лагранжа
а
длина всей ломаной, вписанной в кривую
L, равна
.Из определения длины дуги имеем
. Так как правая часть есть интегральная
сумма для функции
то
2. Длина дуги при параметрическом задании L
3. Длина дуги в полярных координатах
19. Теорема Ролля.
Пусть
функция
непрерывна на сегменте
и дифференцируема во всех внутренних
точках этого сегмента. Пусть, кроме
того,
.
Тогда внутри сегмента
найдется точка
такая, что значение производной в этой
точке
равно нулю. Кратко можно сказать, что
между двумя равными значениями
дифференцируемой функции обязательно
лежит нуль производной этой функции.
Доказательство.
Так как функция
непрерывна
на сегменте
, то, согласно 2-ой теореме Вейерштрасса,
эта функция достигает на этом сегменте
своего максимального значения М и своего
минимального значения m.
Могут представиться два случая: 1) М = m;
2) М >m.
В случае 1)
= М = m
= const. Поэтому производная
равна нулю в любой точке сегмента
.
В случае М > m,
поскольку
,
можно утверждать, что хотя бы одно из
двух значений М или m
достигается функцией в некоторой
внутренней точке
сегмента
.
Но тогда функция
имеет в этой точке
локальный экстремум. Поскольку функция
дифференцируема
в точке
,
то по теореме «если функция
дифференцируема
в точке с и имеет в этой точке локальный
экстремум, то
»
.
Теорема
Ролля имеет простой геометрический
смысл: если крайние ординаты кривой
равны, то, согласно теореме Ролля, на
кривой
найдется точка, в которой касательная
к кривой параллельна оси OX.
20. Теорема Лагранжа.
Если
функция
непрерывна на сегменте
и дифференцируема во всех внутренних
точках этого сегмента, то внутри сегмента
найдется
точка
такая, что справедлива формула
(8.7)
Формулу (8.7) называют формулой Лагранжа или формулой конечных приращений.
Доказательство.
Рассмотрим на сегменте
следующую
вспомогательную функцию:
(8.8)
Проверим,
что для функции
выполнены все условия теоремы Ролля. В
самом деле,
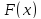непрерывна на сегменте
(как разность функции
и линейной функции) и во всех внутренних
точках сегмента
имеет производную, равную
Из
формулы (8.8) очевидно, что
.Согласно теореме Ролля внутри сегмента
найдется точка
такая, что
(8.9)
Из
равенства (8.9) вытекает формула Лагранжа
(8.7). Подчеркнем, что в формуле (8.7) вовсе
не обязательно считать, что
.
Замечание.
Мы получили теорему Лагранжа как
следствие теоремы Ролля. Заметим вместе
с тем, что сама теорема Ролля является
частным случаем теоремы Лагранжа (при
)
.
Записывая
формулу Лагранжа для сегмента
,
будем иметь
(8.10)
где
– некоторая точка, лежащая между
.
Можно утверждать, что найдется такое
(зависящее от
)
число
из интервала
,
что
.
Таким образом, формуле (8.10) можно придать
вид
(8.11)
где
— некоторое число из интервала
.
Формула Лагранжа в виде (8.11) дает точное
выражение для приращения функции через
вызвавшее его произвольное конечное
приращение
аргумента. Этот вид формулы Лагранжа
оправдывает термин «формула конечных
приращений».
21. Достаточное условие существования экстремумов
Первое достаточное условие экстремума.
Пусть точка С является точкой возможного экстремума функции f(x), и пусть функция f(x) дифференцируема всюду в некоторой окрестности точки С. Тогда, если в пределах указанной окрестности производная f’(x) положительна (отрицательна) слева от точки С и отрицательна (положительна) справа от точки С, то функция f(x) имеет в точке С локальный максимум (минимум). Если же производная f’(x) имеет один и тот же знак слева и справа от точки С, то экстремумов в точке С нет.
Док-во: 1) пусть f’(x) в пределах рассматриваемой окрестности положительна (отрицательна) слева от С и отрицательна (положительна) справа от С. Требуется доказать, что значение f(C) является наибольшим(наименьшим) среди всех значений f(x) в рассматриваемой окрестности. Обозначим x0 любое значение аргумента из рассматриваемой окрестности, отличное от С. Достаточно доказать что
f(c)-f(x0)>0 (<0).
Функция f(x) дифференцируема (а стало быть, и непрерывна) на сегменте[С,x0]. Применяя к f(x) на этом сегменте теорему Лагранжа будем иметь:
f(c)-f(x)=f’(ζ)(C-x0), где ζ –некоторое значение аргумента между C и x0. поскольку f’(ζ) положительна (отрицательна) при x0<C и отрицательна (положительна) при x0>C, правая часть положительна (отрицательна).
2) пусть f’(x) имеет один и тот же знак слева и справа от точки С.
Повторяя проведенные выше рассуждения мы докажем что правая часть f(c)-f(x)=f’(ζ)(C-x0), имеет разные знаки при x0<C и при x0>C. это доказывает отсутсвие экстремума в точке С.
Вытекающее из теоремы f(c)-f(x)=f’(ζ)(C-x0)правило можно кратко сформулировать:
1) если при переходе через данную точку С возможного экстремума производная f’(x) меняет знак с плюса на минус (с минуса на плюс), то функцияf(x) имеет в точке С локальный максимум(минимум)2) если при переходе через данную точку С возможного экстремума производная f’(x) не меняет знака, то экстремума в точке С нет.
Второе достаточное условие экстремума.
Предполагает существование в точке С отличной от нуля конечной второй производной f’’(x).
Теорема. Пусть f(x) имеет в данной точке С возможного экстремума конечную вторую производную. Тогда f(x) имеет в точке С максимум, если f’’(C)<0, и минимум, если f’’(C)>0.
Док-во. f’’(C)<0(>0) f’(x) убывает(возрастает) в точке С. Поскольку f’(c)=0, то найдется такая окрестность точки С, пределах которой f’(x) положительна(отрицательна) слева от С, и отрицательна (положительна) справа от С. Но тогда по предыдущей теореме f(x) имеет в точке С максимум(минимум).
Теорема: Первый достаточный признак экстремума функции.
Если f’(x)>0 на интервале (x0-б,х0) и f’(x)<0 на интервале (х0,x0+б) т.е. меняет знак с плюса на минус при переходе на точку х0, т.е. х0 – точка максимума f(x), а если же меняет знак с минуса на плюс, то х0 – точка минимума.
Доказательство:
.
Теорема: Второй достаточный признак максимума функции
Если f(x) имеет непрерывную вторую производную в окрестности точки х0, и:
1). f’(x0)=0 2). f’’(x0)<0
то х0 точка максимума (аналогично, если f’’(x0)<0, то х0 – точка минимума)
Док-во: Возьмем окрестность, где вторая производная сохраняет знак и запишем формулу Тейлора 1-го порядка для х из данной окрестности.
