39. Энтропия квантовой величины.

Энтропия квантовой величины u*

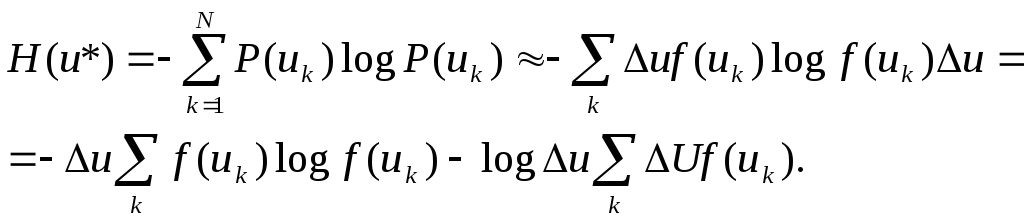
По условию нормирования

тогда

40. Количество информации в непрерывном сообщении. Априорная (безусловная) и апостериорная (условная) дифференциальные энтропии. Симметричность выражения количества информации.

При второе слагаемое стремится к бесконечности. Таким образом, предельный переход не позволяет ввести понятие энтропии переданного сообщения. Однако при определении количества информации для случая, когда сигнал искажен шумами (помехами), нужно из безусловной энтропии H(U) вычесть среднюю условную H_W(Z). В этом случае при квантовании “u” и “” с одинаковым шагом получается, что энтропия соответствующих квантовых величин H(u*) H_W*(U*) имеют одинаковые составляющие - , которые при вычитании взаимно компенсируются. Предельный переход при дает

Величину

(36)

называют априорной (безусловной) дифференциальной энтропией непрерывной величины U.

Величину

(37)

называют апостериорной (условной) дифференциальной энтропией.

Соответственно количество информации есть разность априорной и апостериорной дифференциальной энтропии

(38)

Аналогично можно получить выражение

. (39)

Заметим, что величина дифференциальной энтропии зависит от того, в каких единицах выражена величина переменной. Разность энтропий от этого не зависит, если только величины одинаковы.

Докажем симметричность этого критерия, т.е. что в величине  содержится столько же информации о величине “u”, сколько в величине “u” – о величине . Как и в предыдущем случае, возьмем за основу соотношения, полученные для объектов с дискретными состояниями. Преобразуем формулу (29) для частного количества информации I(u_i):

Подставляя полученное выражение в (34) получим:

Далее найденную формулу применим к непрерывным величинам “u” и “”, подвергнув их квантованию с шагом , и совершив затем предельный переход при .

Тогда получим

(40)

Во многих случаях принимаемую (воспроизводимую) величину  можно представить как сумму передаваемой (измеряемой) величины “u” и некоторой помех “S”:

(41)

причем помеха часто не зависит от “u”. В этом случае условная дифференциальная энтропия равна безусловной энтропии помехи . Покажем это. По аналогии с (37)

(42)

Рассмотрим выражение в квадратных скобках под интегралом в правой части формулы (42). Заменим переменную  в соответствии с (41). При этом . Будем иметь в виду, что данный интеграл вычисляется для фиксированного значения “u”:

Если значение “u” фиксировано, то условная вероятность обращается в безусловную, т.е. .

Тогда

но интеграл в правой части последнего выражения равен единице: . Поэтому

(43)

Формула (39) с учетом (43) имеет вид

(44)

Предполагаем, что при вычислении обеих энтропий – принимаемого сигнала и помехи – величины  и S выражаются в одинаковых единицах.

43. Количество и скорость передачи информации при нормальном распределении сигнала и помехе (погрешности).

Если измеряемая величина “u” и помеха S имеют нормальные распределения, то их сумма также имеет нормальное распределение. Дифференциальная энтропия нормально распределенной величины “u”, вычисленная по формуле (36)

Максимальной дифференциальной энтропией обладает равномерное распределение вероятностей. Если значения случайной величины U лежат в пределах[, ].

где D(u) – дисперсия величины “u”.

Соответственно

Подставляя эти величины в (44), получаем

(45)

Как известно, дисперсия сигнала пропорциональна его средней мощности, которую обозначим P_u, а среднюю мощность помехи P_S. Тогда

(46)

Отметим еще раз, что эта формула справедлива для случая, когда помеха является аддитивной и не зависит от сигнала, а законы их распределения – нормальные.

До сих пор не учитывалось, что “u” есть функция времени, а рассматривалась передача отдельных сообщений о значениях некоторой непрерывной величины “u”. При этом величина I(UW) трактовалась как среднее количество информации, содержащееся в одном принятом значении . Подразумевалось, что усреднение проводится по ансамблю всех возможных значений “u” и  с учетом законов распределения каждой из них отдельно и обеих вместе.

Теперь перейдем к рассмотрению передачи случайной функции времени (случайного процесса) u(t) по каналу, в котором действует случайный шум S(t).

Пусть частотный спектр процесса u(t) ограничен частотой F_max, а ширина полосы частот канала связи не меньше F_max. Согласно теореме Котельникова, указанный процесс u(t) полностью определяется последовательностью ординат взятых с интервалом . Ординаты, отстающие одна от другой на величину Т, статистически взаимно независимы. Поэтому общее количество информации, содержащееся в принятом сообщении, равно сумме количеств информации, содержащихся в этих отдельных ординатах. В сообщении длительностью Т_с содержится 2Т_СF_max таких ординат. Среднее количество информации в принятом сообщении длительностью Т_С равно