20. Частотное представление стационарных случайных сигналов. Дискретные спектры.

Корреляционную функцию R_u() (см. рис. 15) стационарного случайного процесса, заданного на конечном интервале времени [-T, T], можно разложить в ряд Фурье (15), условно считая ее периодически продолжающейся с периодом 4Т (при –T < t₁, t₂ < T, -2T<<2T):

(91)

где _k = k₁, ₁=  / 2T;

По аналогии с (64)

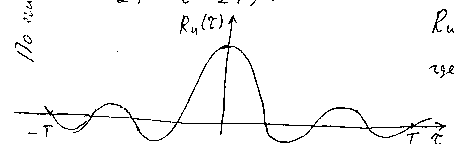
Рис. 15

(92)

Учитывая, что R_u() является четной функцией, имеем

(93)

Положив  = t₁ – t₂, находим

(94)

что согласно (89) представляет собой каноническое разложение корреляционной функции. По нему, как было указано ранее, получаем разложение случайного процесса:

, (95)

причем

(96)

Выражение (95) записано для случайного процесса с нулевой постоянной составляющей, что характерно для многих реальных сигналов. В общем случае в правую часть этого выражения необходимо добавить постоянную величину, соответствующую математическому ожиданию случайного процесса (m_u). Корреляционная функция при этом не изменяется.

Очевидно, что при попарном объединении экспоненциальных составляющих с одинаковыми положительными и отрицательными индексами k каноническое разложение (95) приводится к тригонометрической форме.

Таким образом стационарный случайный процесс на ограниченном интервале времени можно представить совокупностью гармонических составляющих различных частот с амплитудами, являющимися некоррелированными случайными величинами, математические ожидания которых равны нулю.

(96 а)

где

На спектральной диаграмме такого процесса каждой гармонике ставится в соответствие вертикальный отрезок длина которого пропорциональна дисперсии ее амплитуды, а расстояние на оси абсцисс отвечает частоте. (рис. 16)

Рис. 16

Чтобы получить описание стационарного случайного процесса в точном смысле, т.е. справедливое для любого момента времени на бесконечном интервале -<t< необходимо перейти к интегральному каноническому разложению.

21. Частотное представление стационарных случайных сигналов. Непрерывные спектры.

Интегральное каноническое разложение для корреляционной функции получим из формулы (91) путем предельного перехода при Т. Увеличения интервала времени, на котором наблюдается случайный процесс, сопровождающийся уменьшением значений дисперсий, что следует из (92), а также сокращением расстояний между спектральными линиями, поскольку

(97)

При достаточно большом, но конечном Т можно записать выражение для средней плотности распределения дисперсии по частоте:

(98)

где - средняя плотность дисперсии на участке, прилегающем к частоте _k

Теперь можно преобразовать формулы (91) и (98) к виду. D_k подставляем из (92).

(99)

(100)

Переходя к пределу при Т, получаем

(101)

где

(102)

Т.к. величина  являлась не только дисперсией D_k коэффициента разложения корреляционной функции R_u(), но и дисперсией D[C_k] коэффициента разложения случайного процесса U(t), то величина S_uu()d, полученная в результате предельного перехода при Т, представляет собой дисперсию, приходящуюся на спектральные составляющие стационарного случайного процесса, занимающие бесконечно малый интервал частот (, +d). Функцию S_uu(), характеризующую распределения дисперсии случайного процесса по частотам, называют спектральной плотностью стационарного случайного процесса U(t).

Выражение для интегрального канонического разложения корреляционной функции R_u(t) найдем, положив в формуле (101) t = t₁ – t₂ :

(103)

Обозначив и повторив процедуру предельного перехода при Т для соотношения (95), получим каноническое разложение стационарной случайной функции _:

₍₁₀₄₎

_{где дисперсией случайной функции G()d является функция} S_uu(w)dw.