
- •Ен. Ф. 01 математика
- •Введение
- •1 Область определения функции многих переменныx
- •Линии уровня
- •3 Частные производные первого порядка. Полный дифференциал
- •4 Частные производные высших порядков. Дифференциалы высших порядков
- •5 Производные сложных функций
- •Производная по направлению. Градиент
- •Экстремум функции нескольких переменных
5 Производные сложных функций
Пусть z=f(x; y) дифференцируемая функция двух переменных x и y, каждая из которых, в свою очередь, является функцией независимой переменной t:
x=x(t); y=y(t).
z(x(t); y(t)) – сложная функция; x=x(t) и y=y(t) – промежуточные функции. Если они дифференцируемы, то
![]() .
(10)
.
(10)
Производная, найденная по этой формуле, называется полной производной.
Частный
случай, когда t
совпадает
с одним из аргументов, скажем t=x,
а
![]() .
Тогда
.
Тогда
![]() является сложной функцией переменной
x
и
является сложной функцией переменной
x
и
![]() .
(11)
.
(11)
Рассмотрим более сложный случай, когда каждая из переменных х и у, в свою очередь, зависит от двух независимых параметров u и v.
Пусть z=f(x; y), x=x(u; v), y=y(u; v) - дифференцируемые функции своих аргументов. Тогда
![]() и
и
![]() .
(12)
.
(12)
Структура этих формул сохраняется и при большем числе переменных. Например, если w=f(x; y; z), где x=x(t), y=y(t), z=z(t), то
![]() .
(13)
.
(13)
Пример 5.1.
Найти
производную сложной функции
![]()
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Здесь
z
сложная функция одной независимой
переменной t.
По формуле
![]() найдем искомое значение
найдем искомое значение
![]() ,
для этого вычислим все необходимые
частные производные:
,
для этого вычислим все необходимые
частные производные: ![]() ,
, ![]() ;
;
![]() ,
, ![]() .
Тогда
.
Тогда ![]() .
.
Пример 5.2.
Найти
производную сложной функции
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Здесь z сложная функция двух переменных x и y, каждая из которых
зависит
от двух переменных u
и v.
Найдем все необходимые частные
производные: ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Теперь подставим все найденные значения в формулы:
![]() =
=![]()
![]() +
+
![]()
![]() ;
;
![]() =
=
![]()
![]() +
+
![]()
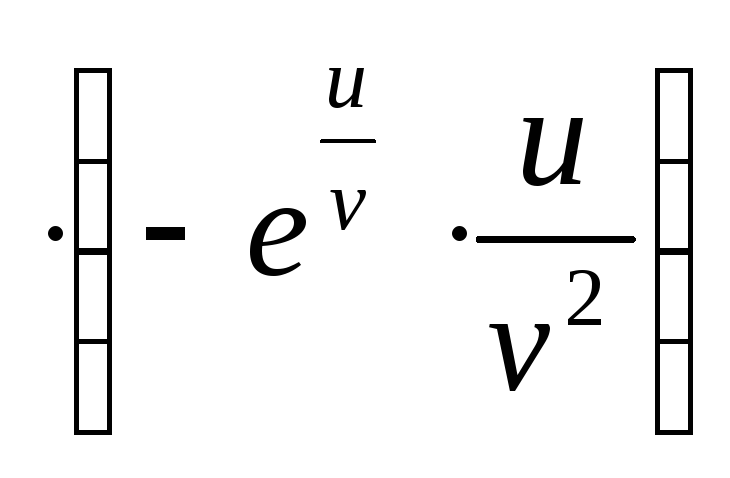 .
.
Пример 5.3.
Найти
производную сложной функции
![]() ,
,
![]() .
.
Решение.
Здесь z сложная функция одной независимой переменной x.
Используем
формулу
![]() .
.
![]() .
.
Задачи для самостоятельного решения:
-
Найти
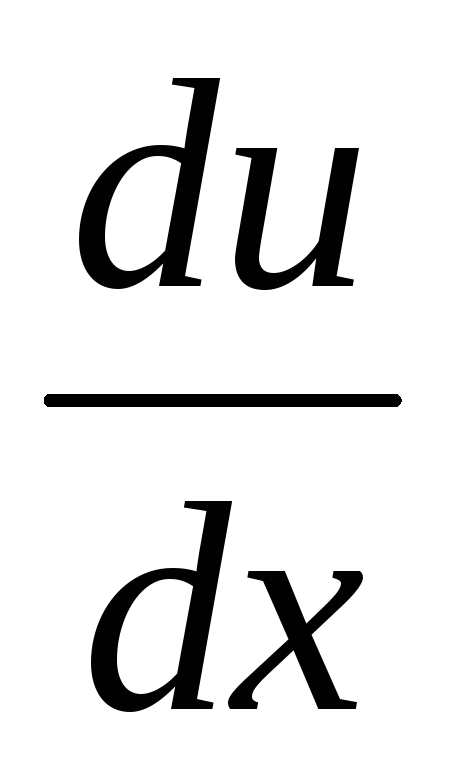 ,
если
,
если
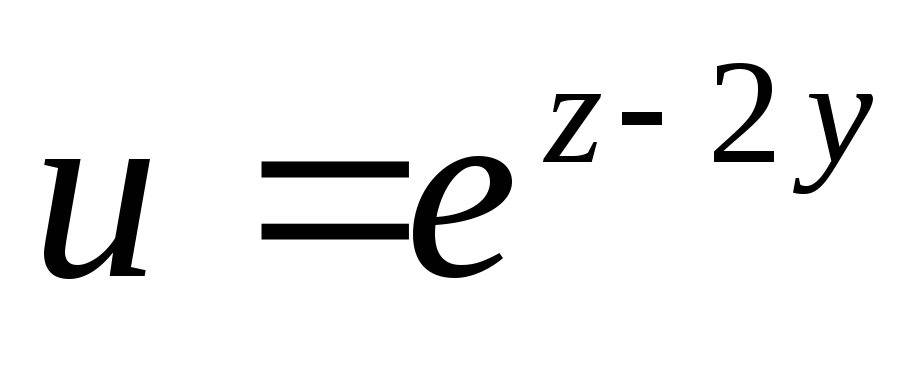 ,
где
,
где
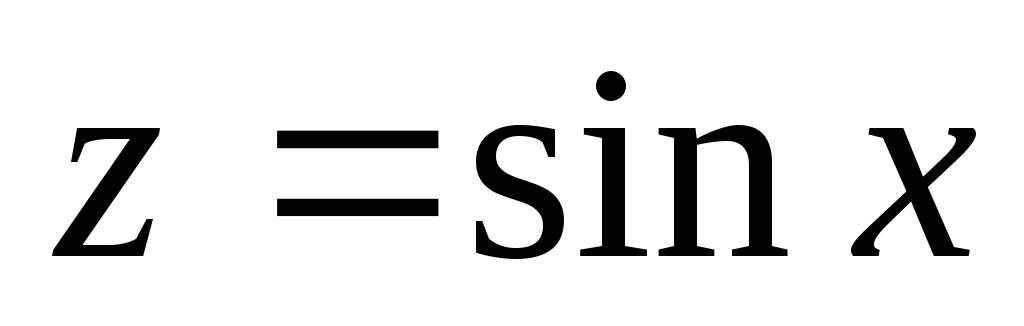 ,
,
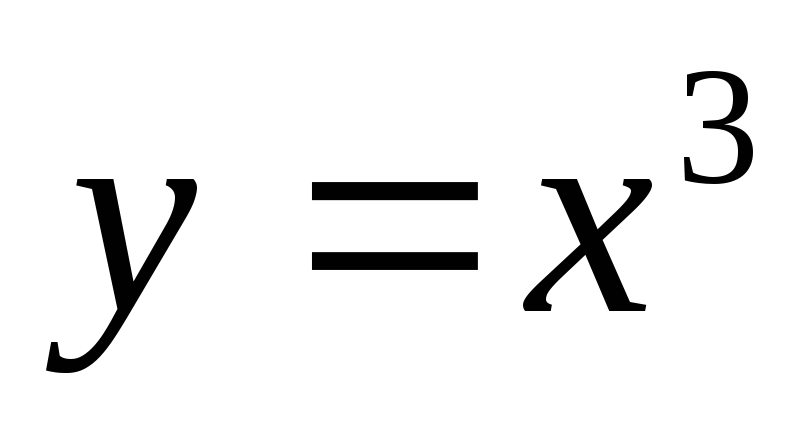 .
. -
Найти
 ,
если
,
если
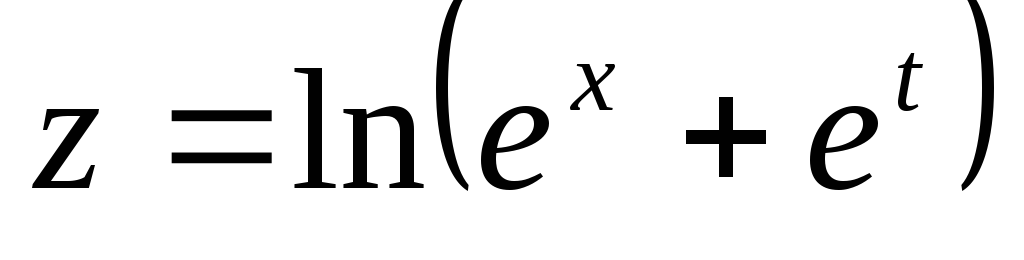 ,
где
,
где

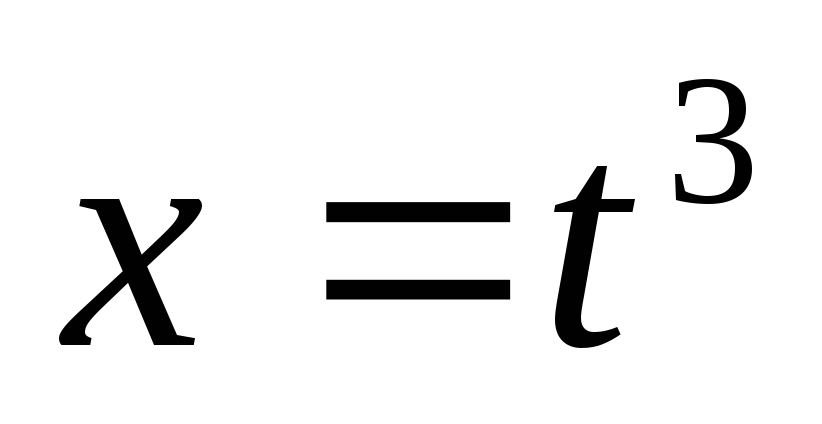 .
. -
Найти
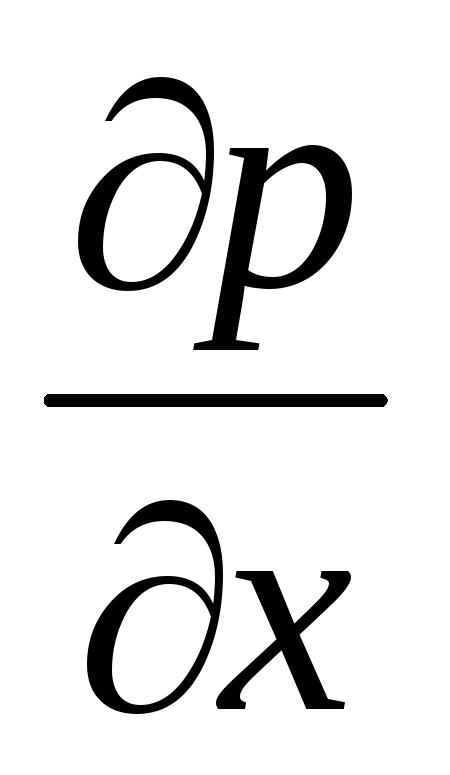 и
и
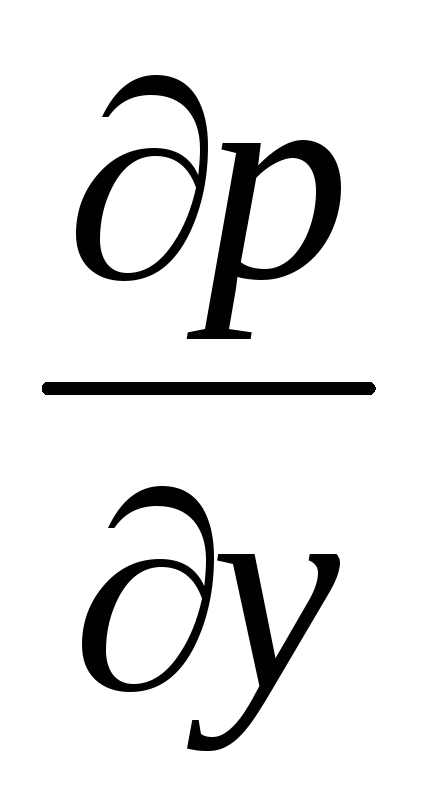 ,
если
,
если
 ,
где
,
где
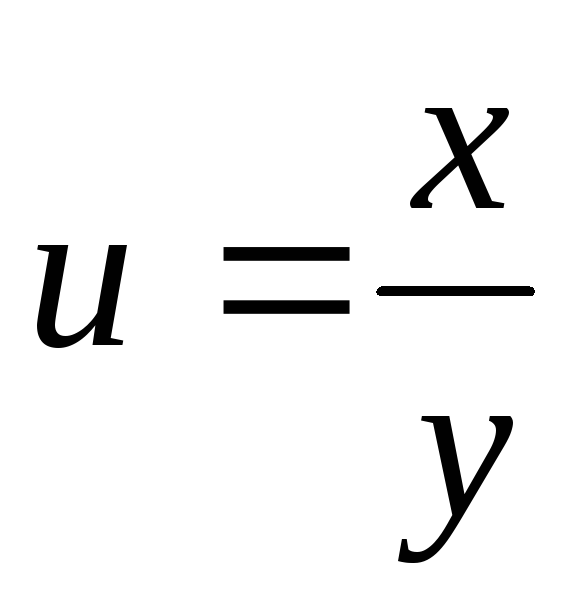 ,
,
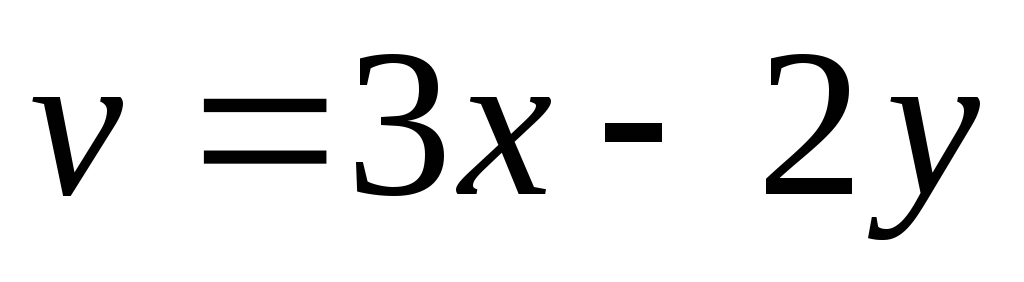 .
. -
Найти
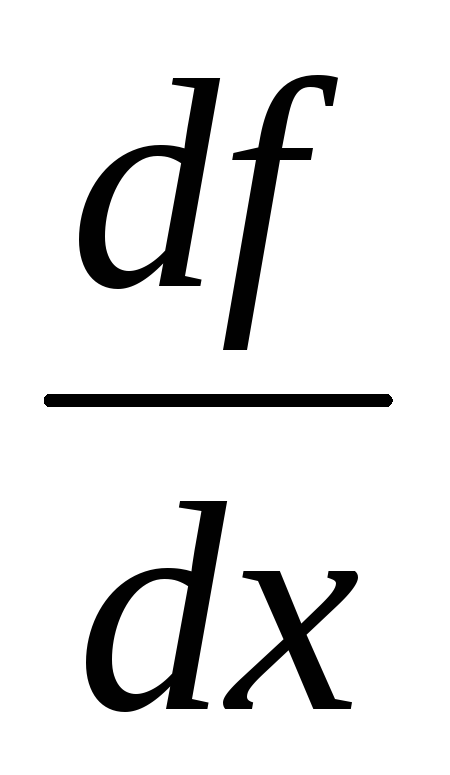 ,
если
,
если
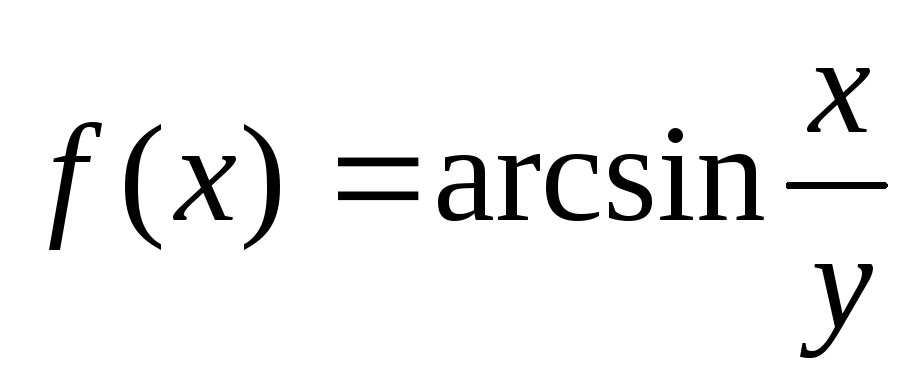 ,
где
,
где
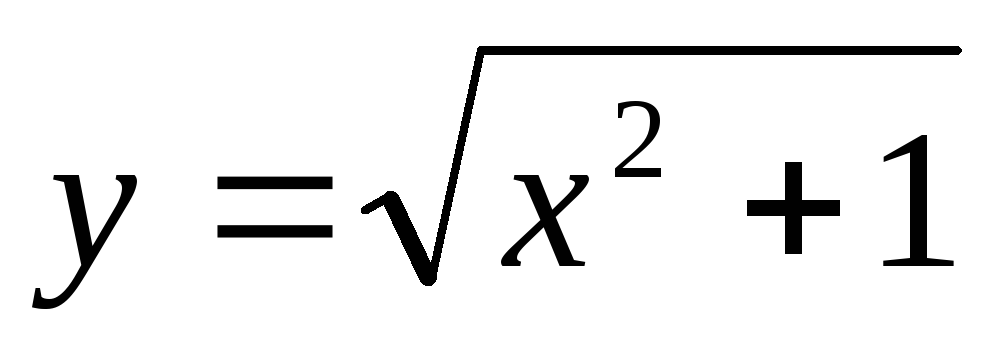 .
. -
Найти
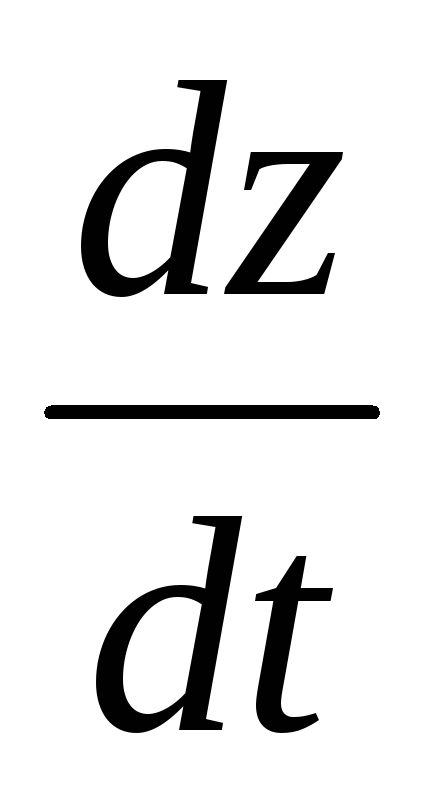 ,
если
,
если
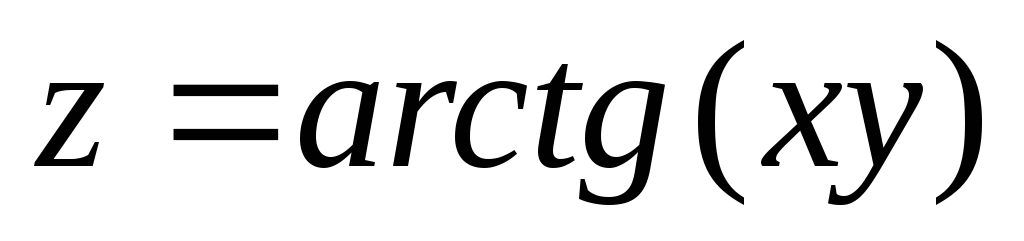 ;
;
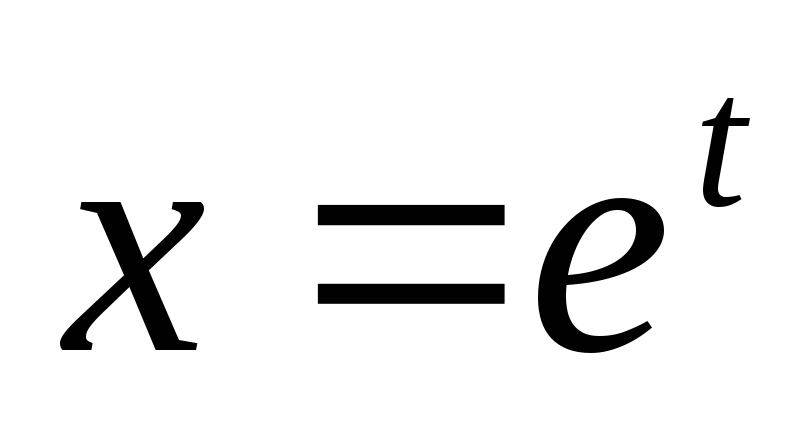 ;
;
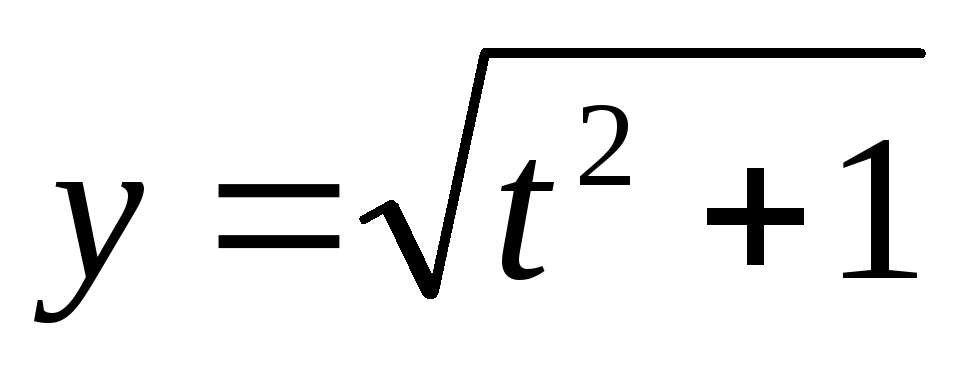 .
.
-
Найти
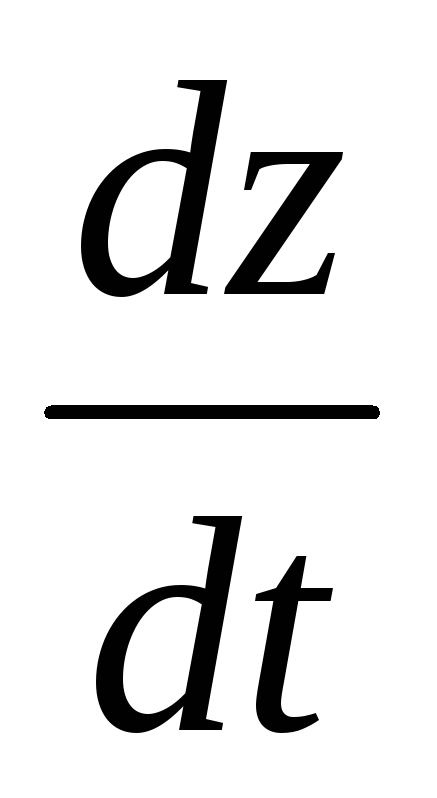 ,
если
,
если
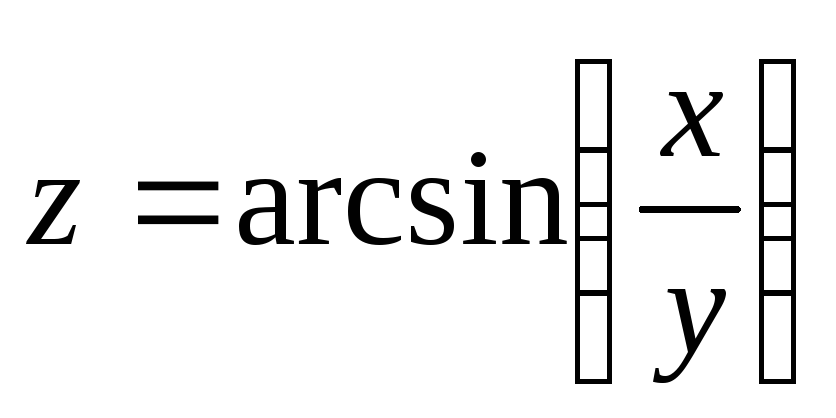 ;
;
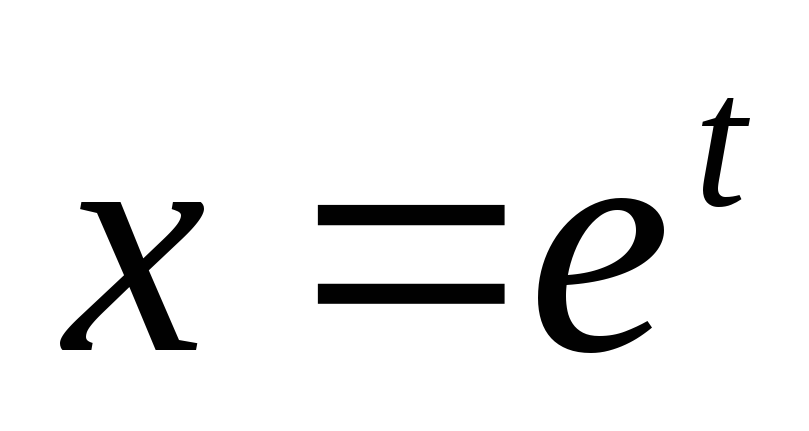 ;
;
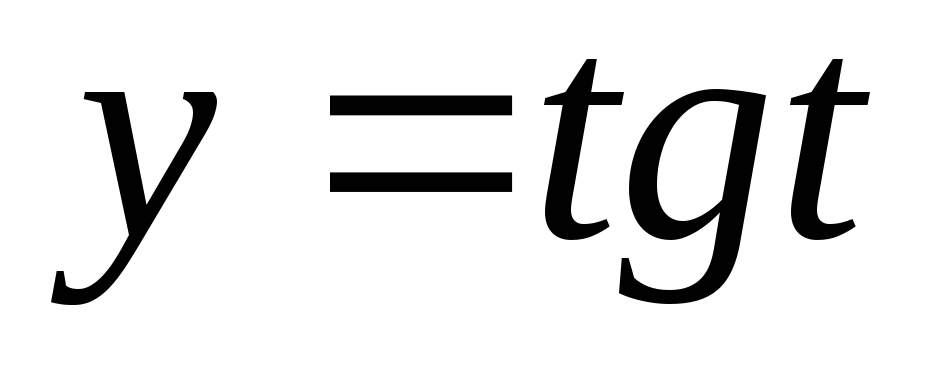 .
. -
Найти
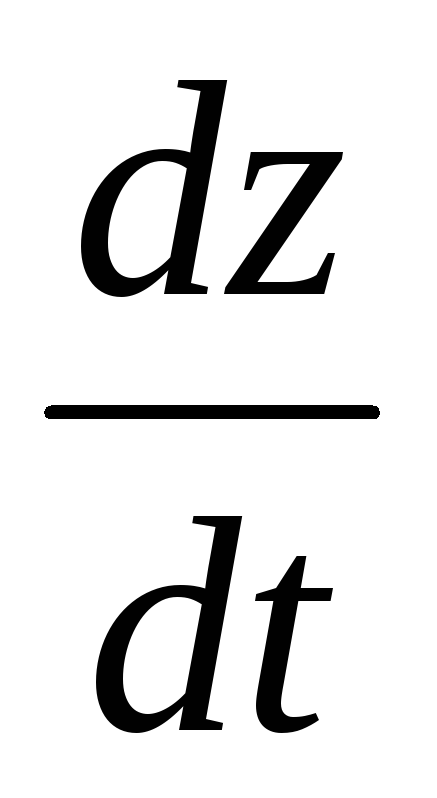 ,
если
,
если
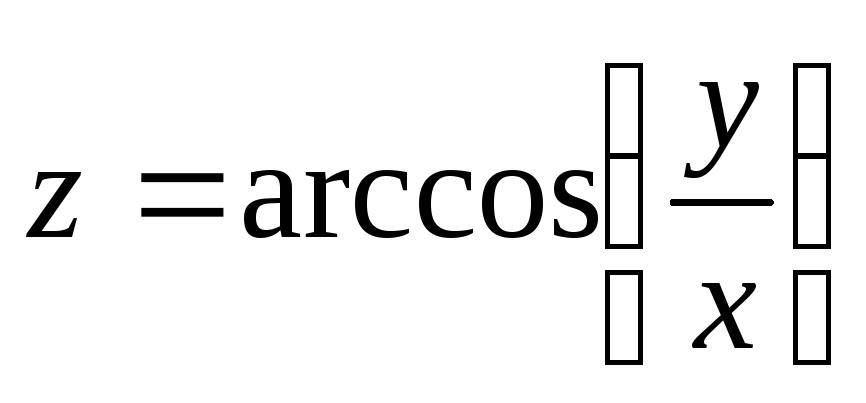 ;
;
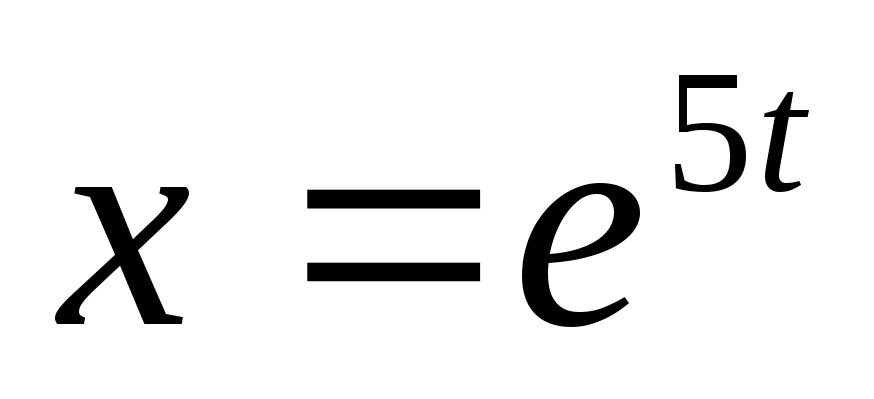 ;
;
 .
. -
Найти
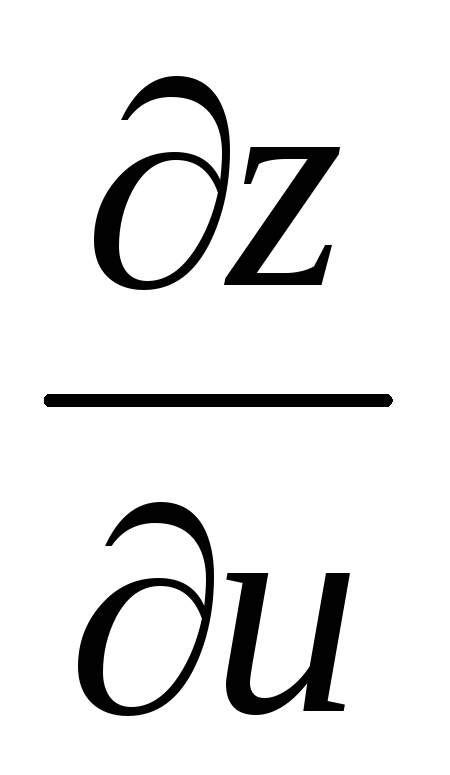 и
и
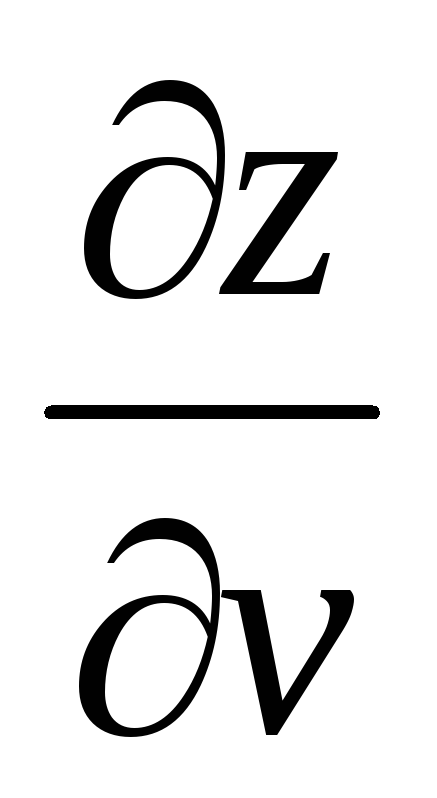 ,
если
,
если
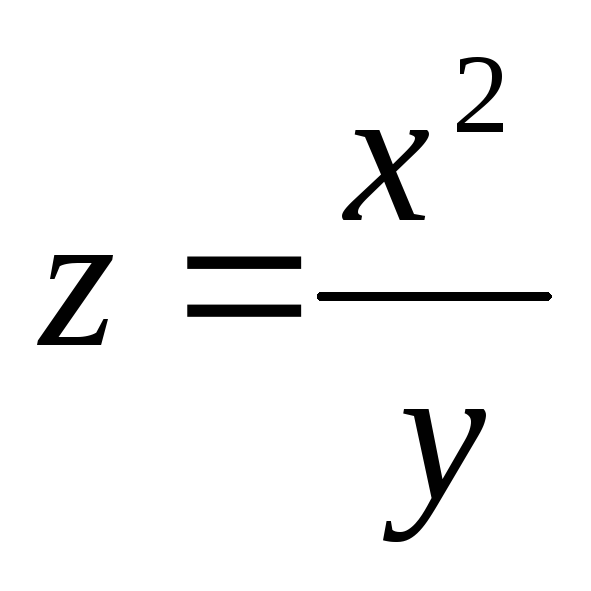 ;
;
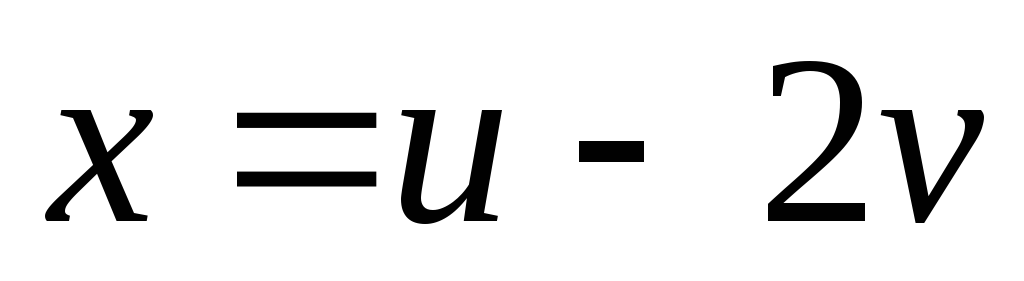 ;
;
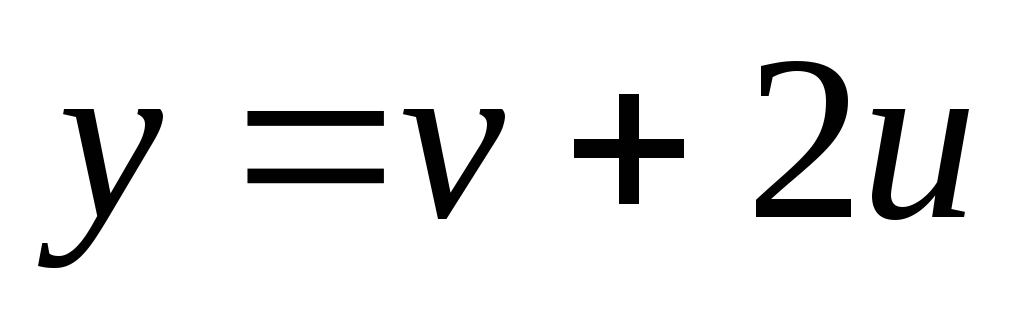 .
. -
Найти
 и
и
 ,
если
,
если
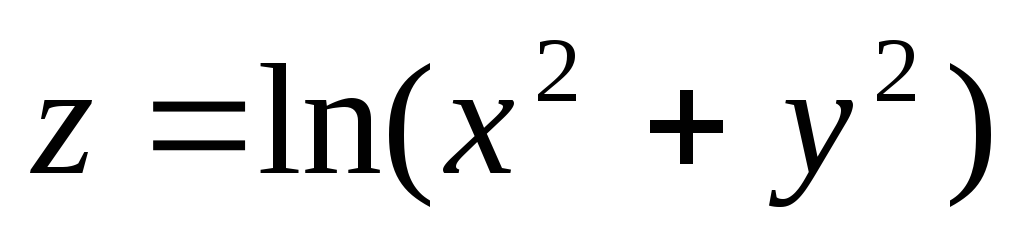 ;
;
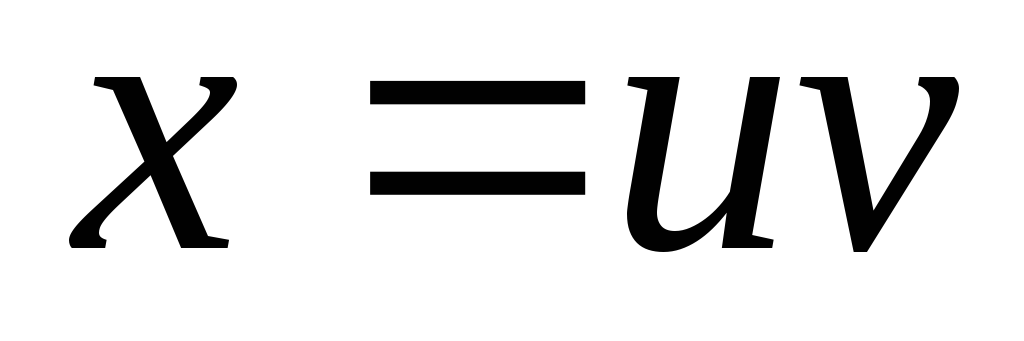 ;
;
 .
. -
Найти
 и
и
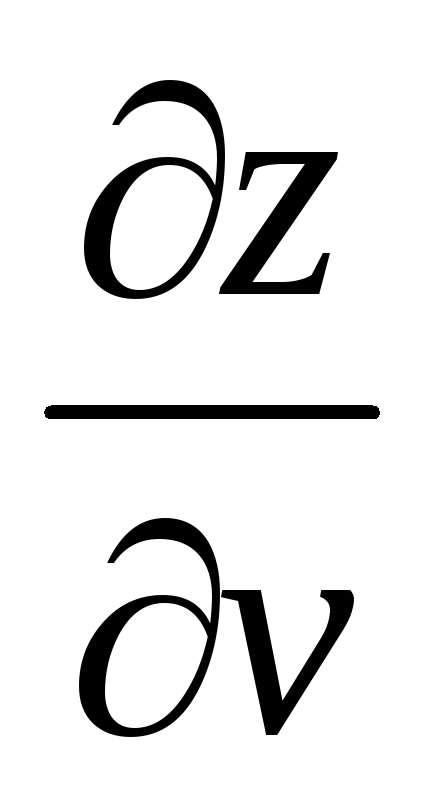 ,
если
,
если
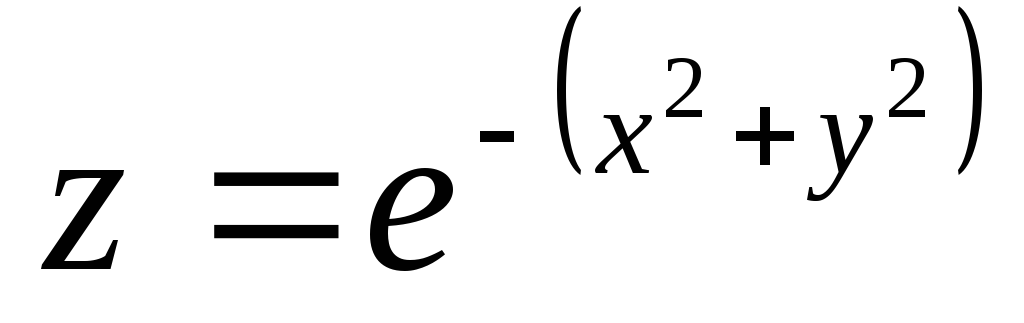 ;
;
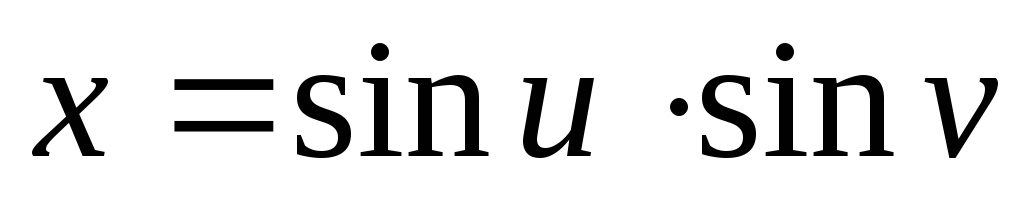 ;
;
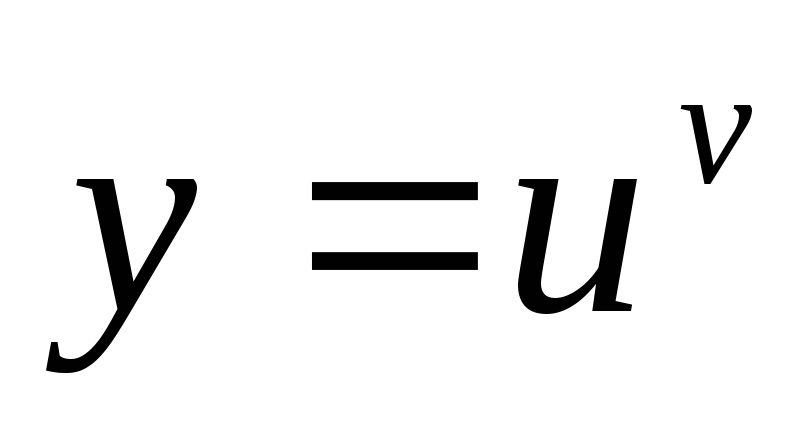 .
.
-
Производная по направлению. Градиент
Частные
производные
![]() и
и
![]() представляют собой производные от
функции z=f(x;
y)
по двум
частным направлениям осей Ox
и Oy.
представляют собой производные от
функции z=f(x;
y)
по двум
частным направлениям осей Ox
и Oy.
Пусть
z=f(x;
y)
– дифференцируемая функция в некоторой
области D,
![]() D.
Пусть
D.
Пусть
![]() -
некоторое направление (вектор с началом
в точке M0),
а
-
некоторое направление (вектор с началом
в точке M0),
а
![]() - орт этого направления.
- орт этого направления.
![]() ,
(14)
,
(14)
при
этом если вектор
![]() =
=![]() ,
то координаты орта (направляющие
косинусы) можно найти по формулам:
,
то координаты орта (направляющие
косинусы) можно найти по формулам:
![]() ,
,
![]() ,
где
,
где
![]() .
.
Теорема. Производная по направлению, касательному к линии уровня поверхности z=f(x; y), равна нулю.
По аналогии можно определить производную по направлению для функции трех переменных u=f(x; y; z):
![]()
![]() ,
(15)
,
(15)
где
![]() - орт направления
- орт направления
![]() .
.
![]()
Градиентом
функции z=f(x;
y)
(скалярного поля) называется вектор с
координатами
![]() ,
,
![]() .
Обозначение
.
Обозначение
![]() .
(16)
.
(16)
Производная
по направлению
![]() равна скалярному произведению векторов
градиента и орта направления
равна скалярному произведению векторов
градиента и орта направления
![]() :
:
![]() .
(17)
.
(17)
Пример 6.1.
Вычислить
производную функции z=2x²+xy
в точке М(-1;
2) в направлении вектора
![]() =3i+4j
и градиент.
=3i+4j
и градиент.
Решение. Найдем значение частных производных в точке М.
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.
Вычислим
направляющие косинусы
![]() =3i+4j
=3i+4j
![]() ;
; ![]() .
.
Тогда: ![]() ;
;
![]() .
.
![]() .
.
![]() .
.
Ответ:
![]() ;
;
![]() .
.
Задачи для самостоятельного решения:
Даны:
функция z=z(x;
y),
точка A
и вектор
![]() .
.
Найти:
а)
![]() в точке A;
в точке A;
б)
производную в точке A
по направлению вектора
![]() .
.
1.
z = ln(5x+3y); A(2;2);
![]() =
=![]() .
.
2.
z = arctg![]() ;
A(2;1);
;
A(2;1);
![]() =
=![]() .
.
3.
z =![]() ;
A(2;1);
;
A(2;1);
![]() =
=![]() .
.
4.
z =
![]() ;
A(2;−1);
;
A(2;−1);
![]() =
=![]() .
.
5.
z
= arcsin![]() ;
A(1;2);
;
A(1;2);
![]() =
=![]() .
.
