Упражнение 7.19

1. Откройте рабочую книгу Функции и добавьте в нее лист Матрицы.

2. В первую строку листа введите заголовок Работа с матрицами.

3. Далее на лист вводите данные и функции, чтобы получить результат аналогичный приведенному ниже рисунку 7.31 .

Рис. 7.31. Примеры использования матричных функций

Пояснения к рисунку.

Введите в диапазон ячеек (A5:C7) матрицу М1, а в диапазон (E5:G7) матрицу М2.

Для нахождения матрицы, обратной для матрицы М1, выделите диапазон ячеек A11: C13, затем с помощью Мастера функций введите функцию МОБР и завершите процесс одновременным нажатием трех клавиш <Ctrl + Shift + Enter>. Аналогичную операцию (но теперь для диапазона E11:G13) проведите для второй матрицы. Сравните полученные результаты с рисунком.

Для нахождения определителя матрицы М1 выделим ячейку A17, введем в нее функцию МОПРЕД и процесс закончим нажатием клавиши <OK>. Выполним аналогичные операции для нахождения определителя второй матрицы, задав ячейку E17. Сравните результаты с рисунком.

Для получения произведения матриц М1 и М2 выделим диапазон ячеек A21:C23, введем функцию МУМНОЖ и завершим процесс одновременным нажатием трех клавиш <Ctrl + Shift + Enter>. Аналогичную операцию только для нахождения произведения матрицы М1 на обратную ей выполним, предварительно выделив диапазон E21:G23. Сравните полученные Вами результаты с результатами на рисунке 7.31.

Функции работы с матрицами эффективны для решения системы линейных уравнений вида методом обратной матрицы:

A₁₁ X₁ + A₁₂ X₂ + …… + A_1N X_N = B₁

A₂₁ X₁ + A₂₂ X₂ + …… + A_2N X_N = B₂

……………………………………………………

A_N1 X₁ + A_N2 X₂ + ……+ A_NN X_N = B_N

В матричном виде такая система уравнений может быть записана следующим образом : A * X = B,

где

A₁₁ A₁₂ …A_1N B₁ X₁

A = A₂₂ A₂₂ …..A_2N B = B₂ X= X₂

…………………….. …. …..

A_N1 A_N2 ……A_NN B_N X₃

Решением системы уравнений будет X = A^-1 * B, где A^-1 - обратная матрица по отношению к A, а B – вектор.

Пример

Используя функции работы с матрицами, решить следующую систему линейных уравнений методом обратной матрицы

Х + 2Y + 8 Z+ 22 = 0

A = X - Y + Z + 2, 5 = 0

10 X - 3 Z - 19 = 0

Пояснения

Открыв рабочую книгу Функции, добавим в нее лист Уравнения и на нем сформируем две матрицы : М1 в диапазоне A19 : C21 и М2 в диапазоне E19 : E21. Далее в диапазоне A26 : C28 найдем матрицу, обратную М1.

Выделив диапазон E26:E28 и перемножив обратную матрицу на матрицу М2, завершив ввод функции МУМНОЖ одновременным нажатием трех клавиш <CTRL + SHIFT + ENTER>, получим искомый результат: X = 1, Y = 0,5 Z = -3. (рис. 7.32)

Рис. 7.32. Решение системы линейных уравнений методом обратной матрицы

Упражнение 7.20

В рабочей книге Функции на листе Уравнения, используя функции для работы с матрицами, решите следующие системы линейных уравнений:

5X + 3Y – Z = 8

2X – 4Y + 3Z = 3

7X + 4Y - 2Z = 9

а)

5X + 7Y - 2Z = 3

2X – 12Y - 8Z = 0

X – 3Y = 0

б)

A + 2B – 3C =4

2A – 8B = 6

3B + 4C = 14

в)

X + 2Y + 4 Z = 9

X + 5Y + 4Z = 6

2X + 5Y + Z - 3 = 0

г)

7X – 8Y + 4Z = 3

11X + 5Y – 6Z = -2

X + 4Y – 3Z = 0

д)

Более общим приемом решения систем линейных уравнений является метод наименьших квадратов, когда число столбцов и строк матрицы не совпадает. Для этого обе части уравнения следует умножить на транспонированную матрицу системы - А^т.

А^тАХ =А^тB

Затем обе части уравнения надо умножить на (А^тА)^-1.

Если эта матрица существует, то система определена. Тогда решение системы получается в виде Х=(А^тА)^-1 *А^тВ.

Ниже рассматривается технология решения систем линейных уравнений методом наименьших квадратов.

Пусть требуется решить систему уравнений

3х + 2у =7

4х – 5у =40

3х + 3у = 3

Последовательность решения системы уравнений следующая.

1. Вводим значения элементов матрицы А в диапазон рабочего листа (А2:B4).

2. Вводим значения элементов вектора B в ячейки рабочего листа D2:D4.

3. Транспонируем исходную матрицу A. Для этого выделяем диапазон размерностью 3 х 2 , например (A6:C7), вводим в него функцию категории Массивы и ссылки =ТРАНСП(A2:B4) и нажимаем комбинацию клавиш <Ctrl + Shift +Enter>. В результате в выделенном диапазоне появится результат транспонирования.

4. Вычисляем произведение двух матриц - A^т и B. Для этого выделяем диапазон из двух ячеек (E6:E7) и вводим в него функцию МУМНОЖ (A6:C7; D2:D4).

5. Вычисляем произведение двух новых матриц - A^т и A. С этой целью выделяем диапазон (A9:B10) и вводим в него функцию МУМНОЖ (A6:C7; A2:B4).

6. Выделяем диапазон (D9:E10), задаем в нем функцию МОБР(A9:B10), чтобы вычислить обратную матрицу (A^тА)^-1.

7. Для вычисления итогового результата, т.е. решения системы линейных уравнений, выделяем диапазон (B12:B13) и вводим в него функцию перемножения матриц МУМНОЖ(D9:E10; E6:E7). Таким образом, в ячейках B12 и B13 будет получен результат решения системы линейных уравнений методом наименьших квадратов.

Ход решения описанной задачи представлен на рис. 7.33.

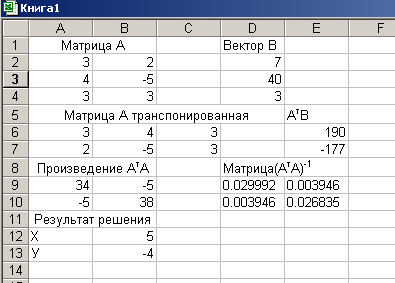
Рис. 7. 33. Результаты решение системы уравнений методом наименьших квадратов