
- •Глава 4 интегрирование функций комплексного переменного
- •§ 1. Определение интеграла от функции комплексного
- •Переменного и его свойства
- •§ 2. Теорема Коши
- •§ 3. Неопределенный интеграл
- •§ 4. Интегральная формула Коши и ее приложения.
- •Теорема Лиувилля
- •Операционное исчисление
- •§ 1. Оригинал и изображение
- •§ 2. Свойства преобразования Лапласа
- •§ 3. Изображение функции Дирака
- •§ 4. Теорема обращения
- •§ 4. Теорема разложения
§ 4. Теорема разложения
Рассмотрим
важный частный случай нахождения
оригинала, когда изображение его
представляет собой правильную рациональную
дробь, т. е.
![]() где
где
![]() и
и
![]() многочлены.
многочлены.
-
Допустим, что корни
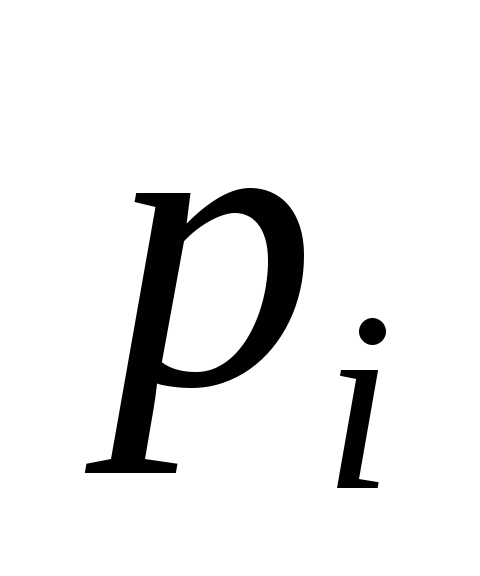 знаменателя
знаменателя
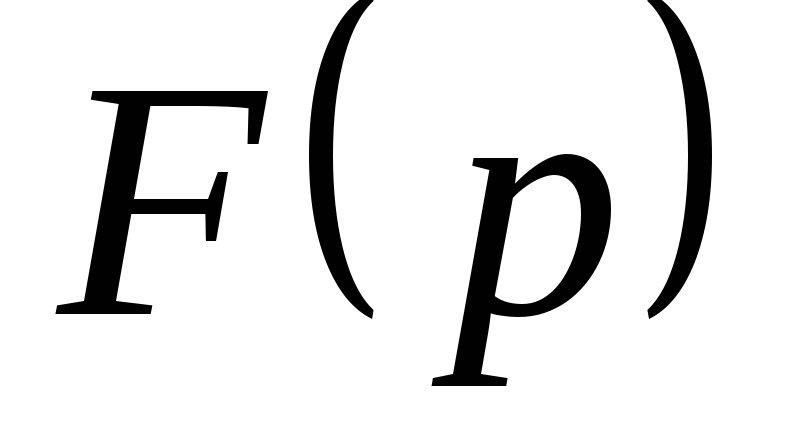 простые.
простые.
Как известно всякую правильную дробь можно представить в виде суммы простейших дробей, т. е.
![]()
![]() (10.11)
(10.11)
Если
известны
![]() и
и
![]() ,
то оригинал определится формулой
,
то оригинал определится формулой
![]()
так как
![]()
Коэффициенты
![]() находятся следующим образом: умножим
(10.11) на
находятся следующим образом: умножим
(10.11) на
![]() и перейдем к пределу при
и перейдем к пределу при
![]() Получим
Получим
![]()
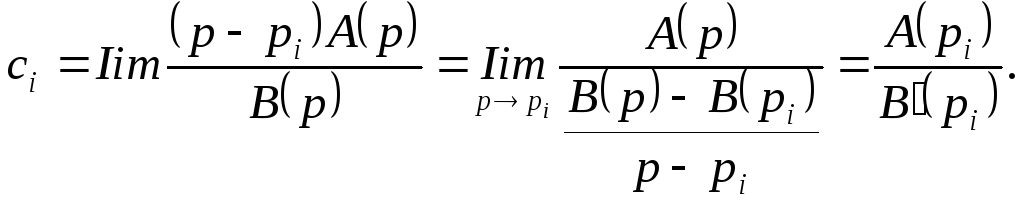
игинал
для
изображения![]() выразится формулой
выразится формулой
 (10.12)
(10.12)
2.
Если же знаменатель
![]() имеет кратные корни, то разложение
дроби
имеет кратные корни, то разложение
дроби
![]() на простейшие имеет вид
на простейшие имеет вид

Умножая
обе части этого равенства на
![]() получим
получим
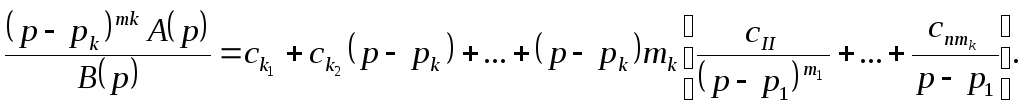 (10.13)
(10.13)
Переходя
к пределу при
![]() ,
найдем в (10.13), будем иметь
,
найдем в (10.13), будем иметь
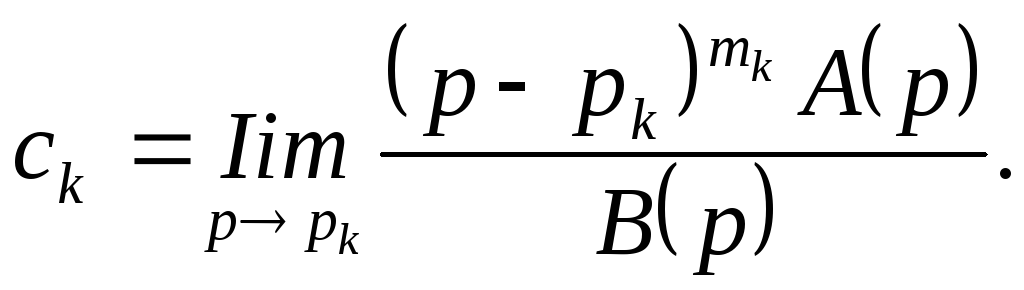
Продифференцировав
равенство (10.13) по
![]() и перейдя к пределу при
и перейдя к пределу при
![]() ,
найдем
,
найдем
![]()
Таким
образом, можно найти все
![]()
![]()
И следовательно, оригинал будет иметь вид
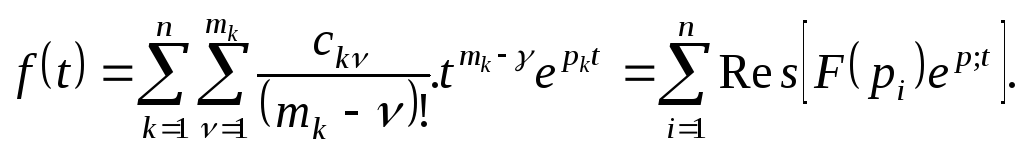 (10.14)
(10.14)
Таким
образом, мы доказали, что если изображение
является дробно- рациональной функцией
и
![]() – полюсы этой функции, то соответствующий
оригинал определяется формулой (10.14),
т. е. в рассматриваемом случае оригинал
может быть найден без формулы (10.8).
– полюсы этой функции, то соответствующий
оригинал определяется формулой (10.14),
т. е. в рассматриваемом случае оригинал
может быть найден без формулы (10.8).
Пример.
![]() Найти оригинал. Имеем
Найти оригинал. Имеем
![]() полюс
третьего порядка,
полюс
третьего порядка,
![]() простой
полюс:
простой
полюс:
![]()
![]()
![]()
![]()
Следовательно,
![]()
Пример. Найти решение уравнения
![]()
удовлетворяющее начальным условиям
![]()
Пусть
![]() ,
тогда уравнение в изображениях будет
иметь вид
,
тогда уравнение в изображениях будет
иметь вид
![]() ,
,
отсюда
![]()
Пользуясь теоремой разложения, получим оригинал, предварительно представив изображение в виде суммы простейших дробей:
![]()
Следовательно,
![]() Таким образом, мы получаем решение
задачи, не находя общего решения
дифференциального уравнения.
Таким образом, мы получаем решение
задачи, не находя общего решения
дифференциального уравнения.
ЛИТЕРАТУРА
1. Лаврентьв М.А. , Шабат Б.В. Методы теории функций комплексного переменного. «Наука», Москва, I 965.
2. Маркушевич А.И. Краткий куре теории аналитических функций. «Наука», Москва, I 966.
3. Свешников А.Г. Тихонов А.В. Теория функций комплексной переменной. «Наука», Москва, I 970.
4. Фукс Б.А.‚ Шабат Б.В. Функции комплексного переменного и некоторые их приложения. Физматгиз. Москва, I 959.
5. Конторович М.И. Операционное исчисление и процессы в электрических цепях. «Наука», Москва, I 964.
