
- •Глава 4 интегрирование функций комплексного переменного
- •§ 1. Определение интеграла от функции комплексного
- •Переменного и его свойства
- •§ 2. Теорема Коши
- •§ 3. Неопределенный интеграл
- •§ 4. Интегральная формула Коши и ее приложения.
- •Теорема Лиувилля
- •Операционное исчисление
- •§ 1. Оригинал и изображение
- •§ 2. Свойства преобразования Лапласа
- •§ 3. Изображение функции Дирака
- •§ 4. Теорема обращения
- •§ 4. Теорема разложения
§ 2. Свойства преобразования Лапласа
Теорема линейности.
Любой
линейной комбинации оригиналов
![]() соответствует такая же линейная
комбинация изображений. Доказательство.
Исходя из определения изображения
(10.1), имеем
соответствует такая же линейная
комбинация изображений. Доказательство.
Исходя из определения изображения
(10.1), имеем
![]()
Пример
![]()
Пример. Найдем изображения тригонометрических и гиперболических функций, применяя теорему линейности
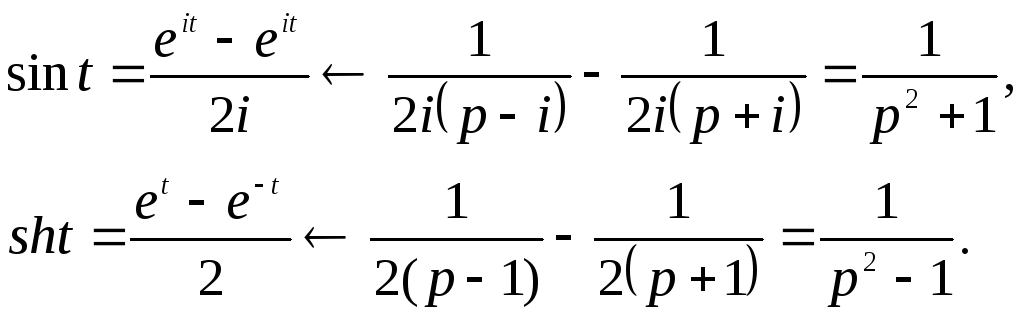
Теорема подобия
Если
![]() и число
и число
![]() то
то
![]()
Доказательство. По определению (10.1)
![]()
В последнем интеграле сделаем замену переменной u = at, тогда
![]()
Пример.
Так как
![]() ,
то следовательно,
,
то следовательно,
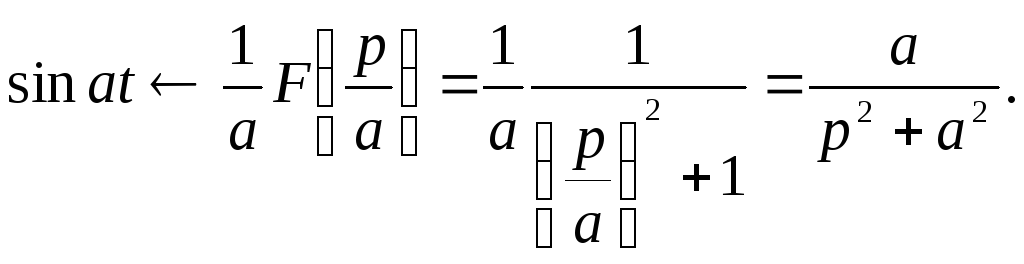
Теорема запаздывания
Если F (p) является изображением для оригинала f (t) и число t0>0, то функция
![]()
![]()
имеет
изображение
![]()
Функцию g (t) можно записать, пользуясь определением единичной функции, так
ơ (t)= ơ (t - t0) f (t - t0).
Графиком функции g (t) является график функции f (t), сдвинутый вправо на t0 вдоль оси t.
Доказательство. Опираясь на равенство (10.1), имеем
ơ
(t
- t0)
f
(t
- t0)![]()
Обозначая
t
– t0
=
![]() ,
получим
,
получим
![]()
Пример. Найдем изображение функции
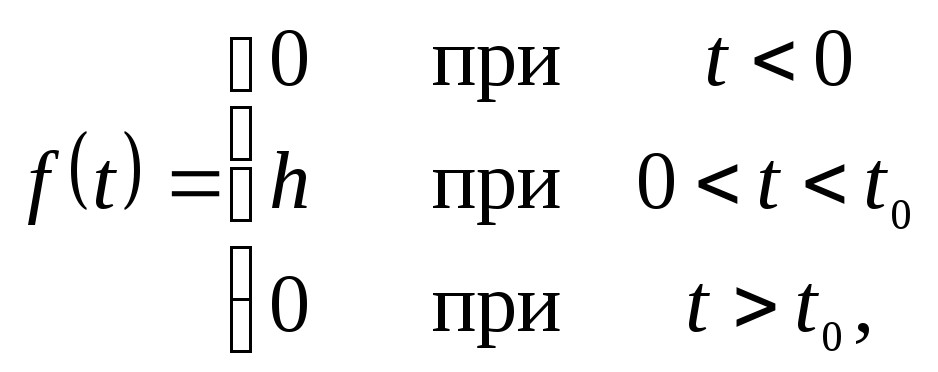
график который изображен на рисунке (10.1)
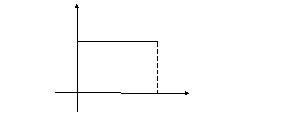
Рис. 10.1
С помощью единичной функции можно данную функцию записать в виде
![]()
Тогда
по теореме запаздывания и зная, что
![]() (t)
(t)![]() ,
будем иметь
,
будем иметь
![]()
Теорема смещения
Если
![]() и
и
![]() -
любое комплексное число, то
-
любое комплексное число, то
![]()
Доказательство. По определению преобразования Лапласа имеем
![]()
Причем изображение F (p - p0) определено при Re (p – p0)> s0 т. е. в полуплоскости
Re p > s0 +Re p0. Теорему смещения можно использовать для отыскания оригинала смещенного изображения F (p – p0), зная оригинал F (p).
Например,
зная изображение для функции
![]() находим изображение для затухшей функции
находим изображение для затухшей функции
![]()
Аналогично, если
![]()
то
![]()
Теорема свертывания
Пусть
f1
(t)![]() F
(p)
и f2
(t)
F
(p)
и f2
(t)![]() F2
(p).
Функция
F2
(p).
Функция
![]() называется свертываемой функцией f1
(t)
и f2
(t)
и обозначается обычно так f1*
f2.
При этом имеет место следующая теорема:
называется свертываемой функцией f1
(t)
и f2
(t)
и обозначается обычно так f1*
f2.
При этом имеет место следующая теорема:
Оригинал, соответствующий произведению двух изображений. Равен свертке оригиналов сомножителей, т. е.
![]()
Доказательство. По определению преобразования Лапласа (10.1) имеем
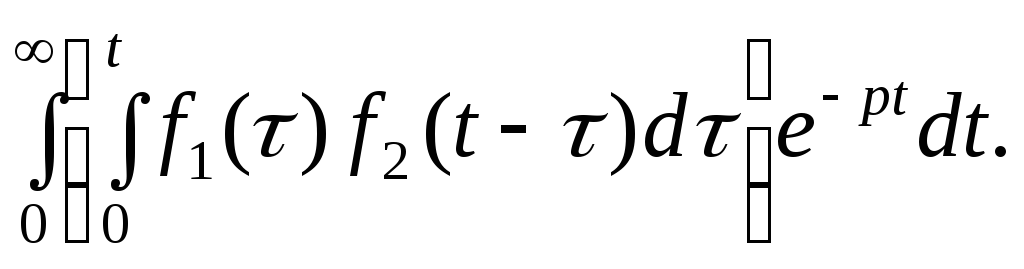
В этом интеграле переменим порядок интегрирования (см. рис. 10.2).
Получим
![]()
Рис. 10.2
Во
внутреннем интеграле произведем
подстановку
![]() тогда получим
тогда получим
![]()
Пример.
Найти
оригинал по его изображению
![]()
Так
как
![]() то на основании теоремы свертывания
то на основании теоремы свертывания
![]()
Теорема дифференцирования оригинала.
Если
![]()
Доказательство.
Преобразованием Лапласа для
![]() является интеграл
является интеграл
![]()
Интегрируя по частям, получим
![]() так
как
так
как
![]() при
при
![]()
Последнее верно, потому что f (t) является оригиналом и, следовательно,
![]()
Последовательным применением этой теоремы можно получить изображения для производных высшего порядка:
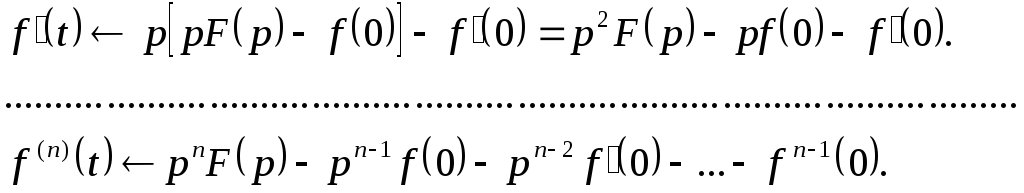
Пример. Найти решение дифференциального уравнения
![]()
тогда
![]()
![]()
![]()
Уравнение в изображениях будет иметь вид
![]()
![]()
Итак,
![]() есть решение данного дифференциального
уравнения.
есть решение данного дифференциального
уравнения.
Следствия. Асимптотическое поведение изображения
-
Если f (t) оригинал, а F (p) аналитическая в бесконечности функция, то
![]() (10.6)
(10.6)
В
самом деле, любое изображение, аналитическое
в бесконечности, стремиться к нулю при
![]() Поэтому изображение функции
Поэтому изображение функции
![]() равное
равное
![]() стремится к нулю при
стремится к нулю при
![]() т. е.
т. е.
![]() Откуда следует равенство (10.6).
Откуда следует равенство (10.6).
Пользуясь
этим предельным соотношением, можно
найти начальное значение оригинала
![]() по его изображению
по его изображению
![]() не вычисляя самого оригинала.
не вычисляя самого оригинала.
-
Если
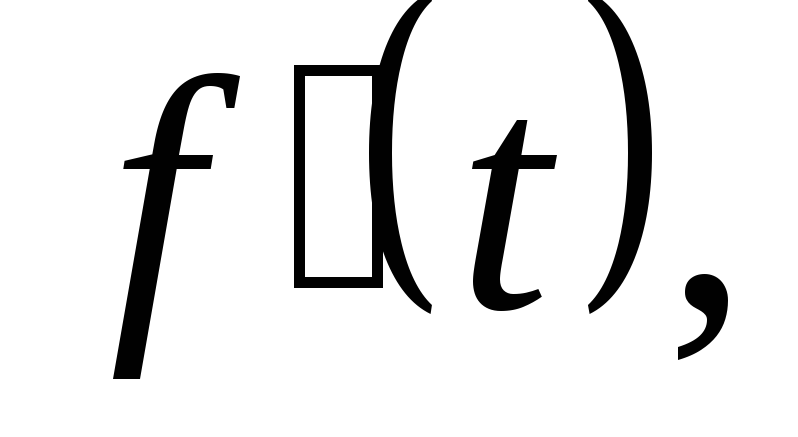 оригинал и существует предел
оригинал и существует предел
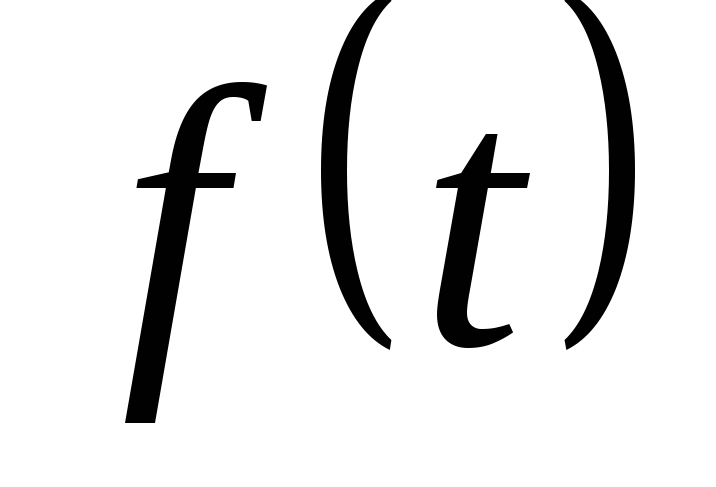 при
при
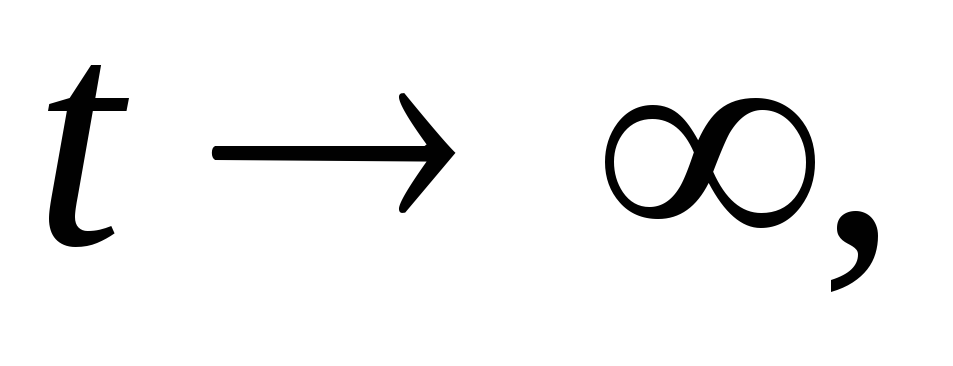 то
то
![]() (10.7)
(10.7)
Воспользуемся теоремой о дифференцировании оригинала
![]()
Перейдем
к пределу при
![]()
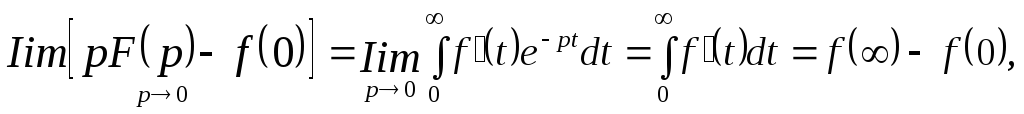
отсюда имеем
![]()
так
как
![]() по предположению существует. (Возможность
перехода к пределу под знаком интеграла
можно обосновать.)
по предположению существует. (Возможность
перехода к пределу под знаком интеграла
можно обосновать.)
Теорема интегрирования оригинала.
Если
![]()
Доказательство.
Пусть изображением
![]() является функция Ф
(p).
Тогда по теореме дифференцирования
оригинала будем иметь
является функция Ф
(p).
Тогда по теореме дифференцирования
оригинала будем иметь
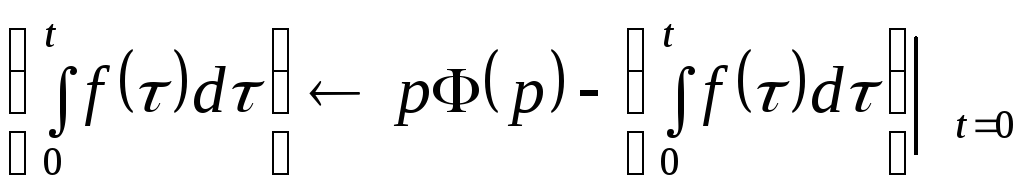 ,
,
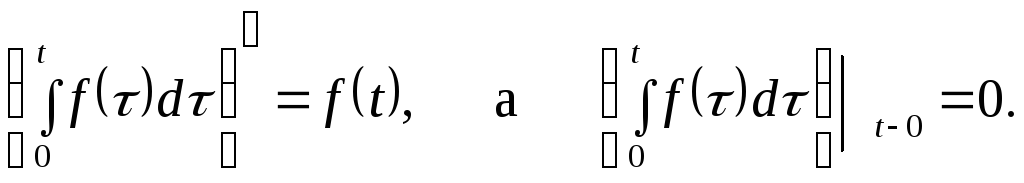
Следовательно,
![]() то есть
то есть
![]()
Итак,
![]()
Пример.
Найти
оригинал по его изображению
![]()
Так
как
![]() то
то
![]()
Теорема дифференцирования изображения
Если
![]()
Доказательство. Пользуясь равенством (10.1) напишем
![]()
Продифференцируем по параметру p это выражение
![]()
А
это и означает, что
![]() является изображением для
является изображением для
![]()
Пример.
Зная, что
![]() и применяя теорему дифференцирования
изображения, получим
и применяя теорему дифференцирования
изображения, получим
![]()
![]()
Теорема интегрирования изображения
Если
![]() и
и
![]() сходится, то
сходится, то
![]()
Доказательство.
Пусть изображением для
![]() является функцией
является функцией
![]() Тогда по теореме дифференцирования
изображения
Тогда по теореме дифференцирования
изображения
![]() т. е.
т. е.
![]()
Интегрируя
последнее равенство от p
до q
и переходя к пределу при
![]() получим
получим
![]()
или же
![]()
Здесь
мы воспользовались тем, что
![]() при
при
![]() что следует из (10.3).
что следует из (10.3).
Пример.
Найти
изображение функции
![]()
Так
как
![]() то
то
![]()
