
- •Глава 4 интегрирование функций комплексного переменного
- •§ 1. Определение интеграла от функции комплексного
- •Переменного и его свойства
- •§ 2. Теорема Коши
- •§ 3. Неопределенный интеграл
- •§ 4. Интегральная формула Коши и ее приложения.
- •Теорема Лиувилля
- •Операционное исчисление
- •§ 1. Оригинал и изображение
- •§ 2. Свойства преобразования Лапласа
- •§ 3. Изображение функции Дирака
- •§ 4. Теорема обращения
- •§ 4. Теорема разложения
§ 3. Неопределенный интеграл
В
интеграле
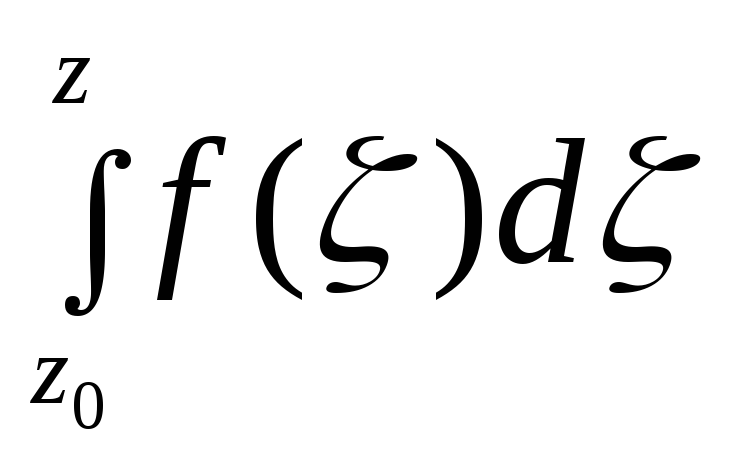 зафиксируем
нижний придел z0
интегрирования и будем рассматривать
интеграл как функцию верхнего предела
зафиксируем
нижний придел z0
интегрирования и будем рассматривать
интеграл как функцию верхнего предела
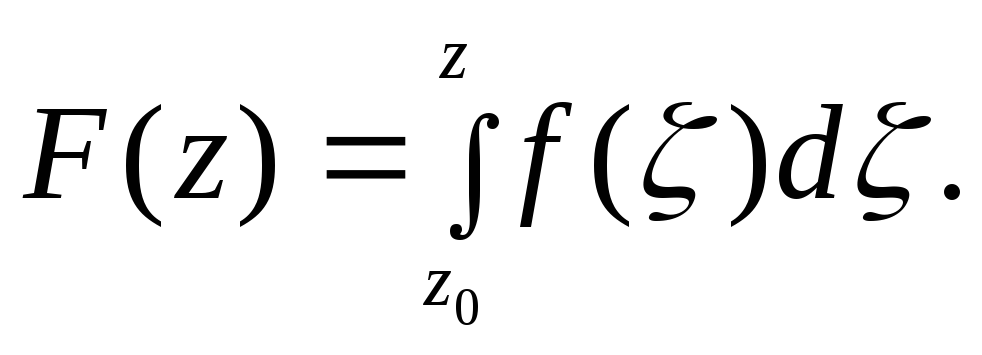 Тогда для функции f
(z)
можно доказать теорему.
Тогда для функции f
(z)
можно доказать теорему.
Теорема.
Если функция f (z) непрерывна в односвязной области D и интеграл
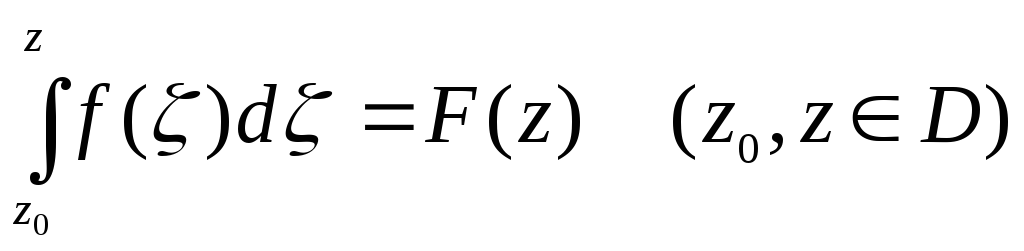 (4.10)
(4.10)
не
зависит от пути интегрирования, то
однозначная в области D
функция f
(z)
аналитична в D,
причем
![]()
Доказательство. По определению производной и на основании свойств интеграла можем записать
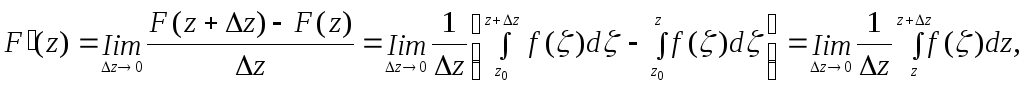

Рис. 4.4
где
z
– произвольная точка D,
![]() (рис. 4.4). В силу непрерывности функции
f(z)
(рис. 4.4). В силу непрерывности функции
f(z)
в точке z имеем
![]()
где
![]() при
при
![]() .
.
Учитывая это, получим:

но
![]() при
при
![]() .
.
(путь
интегрирования от точки z
до точки
![]() считаем прямолинейным).
считаем прямолинейным).
Отсюда
![]() и,
следовательно,
и,
следовательно,
![]()
Функция
Ф(z)
называется первообразной для функции
f(z)
в некоторой области D,
если (Ф(z))′=
![]() для
для
![]() .
.
Из
доказанной теоремы следует, что
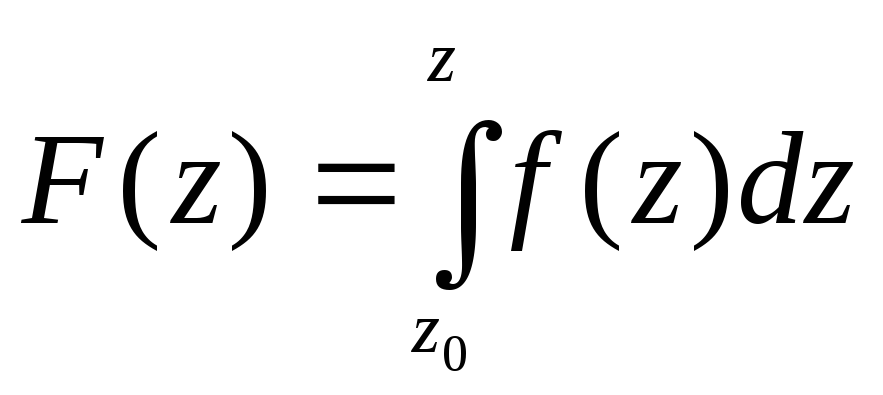 является первообразной для функции
f(z).
Можно легко доказать следующую теорему.
является первообразной для функции
f(z).
Можно легко доказать следующую теорему.
Теорема.
Любые две первообразные одной и той же функции отличаются друг от друга не более, чем на постоянное слагаемое.
Доказательство предоставляется провести самостоятельно.
На основании этой теоремы можно записать:
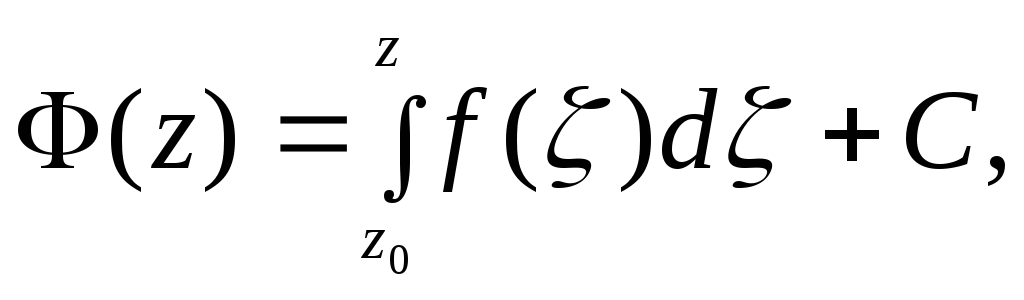 где
Ф(z)
– любая первообразная функция
где
Ф(z)
– любая первообразная функция![]()
При
![]() следовательно,
следовательно,
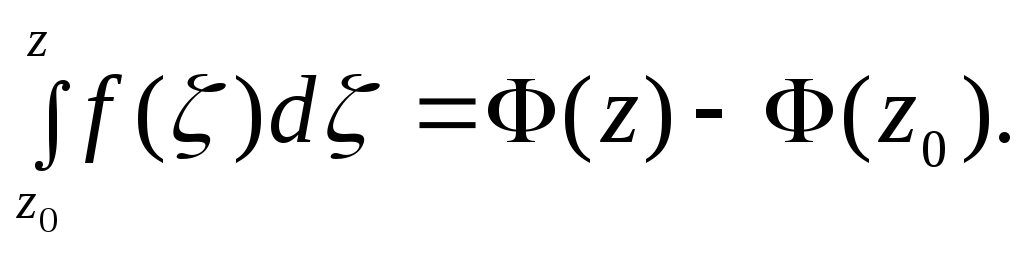 (4.11)
(4.11)
Мы получили формулу, аналогичную формуле Ньютона-Лейбница для вычисления определенного интеграла функции действительного переменного.
Пример.
Рассмотрим
![]() .
Подынтегральная функция аналитична в
любой односвязной области D
комплексной плоскости, не содержащей
току z
= 0, например, в области
.
Подынтегральная функция аналитична в
любой односвязной области D
комплексной плоскости, не содержащей
току z
= 0, например, в области
![]() .
В этой области
.
В этой области
![]() является первообразной для функции
является первообразной для функции
![]() Поэтому
Поэтому
![]() Предположим теперь, что линия,
соединяющая точку z
= 1 с точкой z,
пересекает отрицательную
Предположим теперь, что линия,
соединяющая точку z
= 1 с точкой z,
пересекает отрицательную
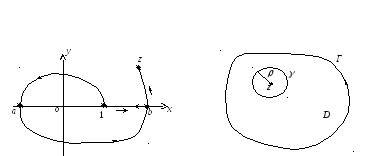
Рис.4.5 Рис.4.6
действительную ось (рис. 4.5). В этом случае, учитывая пример 1 § 1, будем иметь
![]()
Если
путь интегрирования совершает k
оборотов вокруг точки z
= 0, то
![]() (знак определяется направлением движения
по кривой). Таким образом, мы получаем
ту или иную ветвь многозначной функции
Lnz
. Можно написать
(знак определяется направлением движения
по кривой). Таким образом, мы получаем
ту или иную ветвь многозначной функции
Lnz
. Можно написать
![]() .
.
§ 4. Интегральная формула Коши и ее приложения.
Интегральная формула Коши.
Пусть
Г
кусочно-гладкая граница односвязной
области D
и f(z)
– функция, аналитическая в области D
и непрерывная
в замкнутой области
![]()
Рассмотрим
произвольную точку
![]() :
:
Функция
переменной
![]() аналитична всюду в области D
за исключением точки
аналитична всюду в области D
за исключением точки
![]() .
.
Опишем
окружность
![]() радиуса р
с центром в точке z,
принадлежащую области D
(рис. 4.6).
радиуса р
с центром в точке z,
принадлежащую области D
(рис. 4.6).
Так
как функция f(z)
аналитична в двухсвязной области
ограниченной Г
и
![]() ,
и непрерывна на ее границе
,
и непрерывна на ее границе
![]() ,
то по теореме Коши
,
то по теореме Коши
![]() ,
т.е. интеграл
,
т.е. интеграл
![]() не зависит от радиуса р
окружности. Так как существует
не зависит от радиуса р
окружности. Так как существует
![]() ,
то доопределив функцию
,
то доопределив функцию
![]() в точке
в точке
![]() ,
положив
,
положив
![]() ,
будем иметь функцию
,
будем иметь функцию
![]() ,
непрерывную в области D,
а значит и ограниченную в ней:
,
непрерывную в области D,
а значит и ограниченную в ней:
![]() .
.
Учитывая это, получим:
![]()
В силу произвольности р и постоянства M
![]() т.е.
т.е.
![]() или
или
![]()
отсюда получаем интегральную формулу Коши:
![]()
т.е.
значение функции f(z),
аналитической в области D
непрерывна в
![]() ,
можно выразить чрез ее значения на
границе области Г.
,
можно выразить чрез ее значения на
границе области Г.
Пример
1. Вычислить
интеграл
![]()
Т.
к.
![]() аналитична в замкнутой области,
ограниченной окружностью
аналитична в замкнутой области,
ограниченной окружностью![]() ,
то по интегральной формуле Коши имеем:
,
то по интегральной формуле Коши имеем:
![]()
Если рассмотреть этот же интеграл, но в качестве контура взять
окружность
![]() то
то

т.
к. подынтегральная функция аналитична
всюду в замкнутой области, ограниченной
окружностью
![]()
Правую
часть интегральной формулы Коши
![]() называют интегралом Коши.
называют интегралом Коши.
Следствие
1. В частном
случае, если кривая Г
является окружностью с центром в точке
z
радиуса R,
т. е.
![]() мы имеем
мы имеем
![]() и тогда
и тогда
![]()
т.
е. f
(z)
есть среднее арифметическое значение
f
(![]() )
на окружности центром z.
)
на окружности центром z.
Интегральная
формула Коши справедлива и для многосвязной
области. Действительно, пусть D
многосвязная область, ограниченная
контуром
![]() и функция f
(z)
аналитична в D
и непрерывна
и функция f
(z)
аналитична в D
и непрерывна
![]() .
.

Рис. 4.7.
Рассмотрим
произвольную точку
![]() .
Окружим точку z
окружностью CR,
так, чтобы область, ограниченная
окружностью CR
, вместе с самой окружностью полностью
принадлежала D
(рис. 4.7). Тогда функция
.
Окружим точку z
окружностью CR,
так, чтобы область, ограниченная
окружностью CR
, вместе с самой окружностью полностью
принадлежала D
(рис. 4.7). Тогда функция
![]() удовлетворяет условиям теоремы Коши в
(m
+ 2)-связной
области ограниченной контуром
удовлетворяет условиям теоремы Коши в
(m
+ 2)-связной
области ограниченной контуром
![]() и следовательно,
и следовательно,
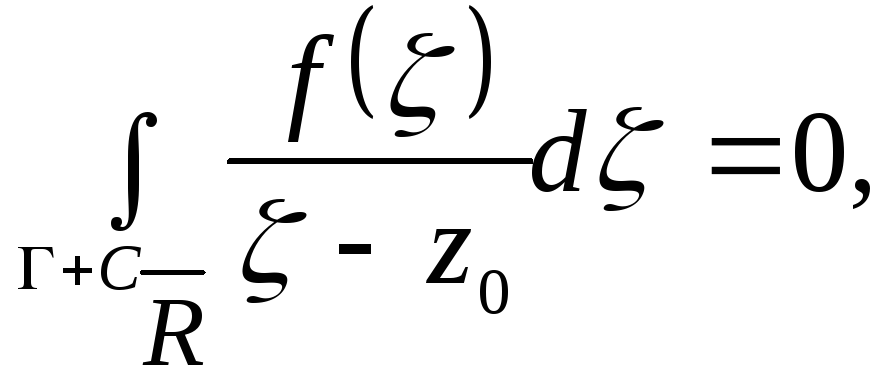 или
или
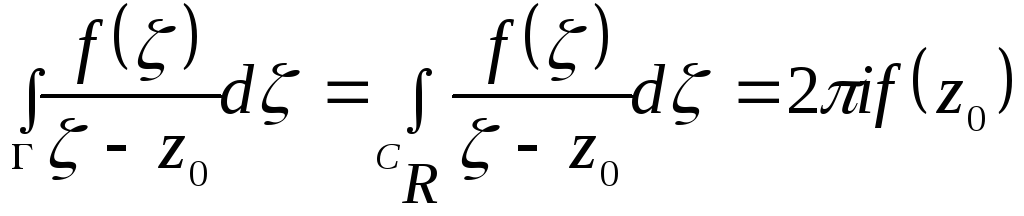
на основании доказанной выше теоремы.
Отсюда
![]()
Неограниченная дифференцируемость аналитической
функции
Используя представление функции интегралом Коши (6.6), можно показать, что аналитическая в области в функция дифференцируема в точках области D сколько угодно раз.
Теорема.
Если функция f
(z)
аналитична в области D
и непрерывна в области
![]() ,
то она обладает в области D
производными всех порядков, причем n-ая
производная представляется формулой
,
то она обладает в области D
производными всех порядков, причем n-ая
производная представляется формулой
![]() (6.7)
(6.7)
где Г - граница области D.
Рис. 4.8
Доказательство.
Пусть z
– произвольная точка области D
(Pис.4.8).
На основании интегральной формулы Коши
имеем
![]()
![]()
Оценим разность
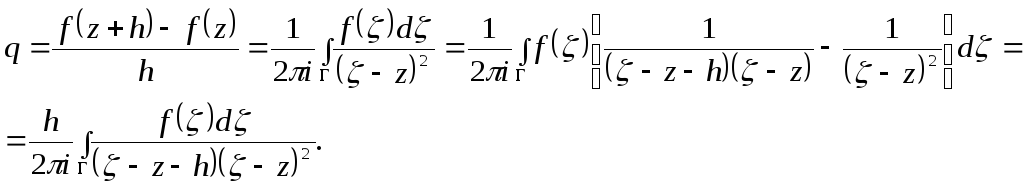
Из
непрерывности f
(z)
на замкнутом множестве Г
следует ограниченность f
(z)
на Г,
т.е. существует М
>0 такое, что
![]() < М
для
< М
для
![]() С другой стороны
С другой стороны
![]() поэтому существует
поэтому существует
![]() такое, что
такое, что
![]() .
Тогда для
.
Тогда для
![]() имеем
имеем
![]()
Отсюда
![]()
Где
l
- длина Г.
Т. к. M,
l,
d
не зависят от L,
то при
![]()
![]() .
Следовательно,
.
Следовательно,
![]()
Мы доказали формулу (6.7) для n = 1.
Для любого n > 1 формула доказывается индукцией по n.
Пример
2. Вычислить
![]() К этому интегралу можно применить
формулу (6.7), тогда
К этому интегралу можно применить
формулу (6.7), тогда
![]()
Замечание: неравенства Коши.
Обозначим
через М
максимум
![]() в
области D,
через R
расстояние от точки z
до границы и через l
длину границы Г,
тогда из интегральной формулы для n-ой
производной имеем:
в
области D,
через R
расстояние от точки z
до границы и через l
длину границы Г,
тогда из интегральной формулы для n-ой
производной имеем:
![]()
В
частности, если (z)
аналитична в круге
![]() ,
то принимая в качестве D
этот круг, будем иметь:
,
то принимая в качестве D
этот круг, будем иметь:
![]() (n
= 0, 1, 2…). (6.8)
(n
= 0, 1, 2…). (6.8)
Эти неравенства называют неравенствами Коши.
