Теорема Лиувилля

Если f (z) аналитична во всей плоскости и ограничена, то она постоянна.

Доказательство. Пусть , тогда на основании неравенства Коши (6.3) для и при п = 1 имеем , но так как левая часть неравенства не зависит от R, а правая при , то . Таким образом f (z) = 0 во всей плоскости.

Используя формулу Лейбница (6.5), имеем

т. е. для

функция во всей комплексной плоскости.

Отметим без доказательства еще две теоремы.

Обращение теоремы Коши (теорема Морера).

Если функция f (z), непрерывная в односвязной области D, для всякого кусочно-гладкого замкнутого контура Жордана Г, лежащего в области D, удовлетворяет равенству , то f (z) аналитична в области.

Теорема (принцип максимума модуля).

Если функция f (z), не равная тождественно постоянной, аналитична в области D и непрерывная в , то ее модуль не может достигать наибольшего значения во внутренней точке области D. (Аналогичное утверждение справедливо для минимума при дополнительном условии для ).

Операционное исчисление

Современные расчеты разнообразных механических, электрических, гидравлических систем не могут выполняться без изучения переходных процессов в этих системах. Операционное исчисление является удобным аппаратом аналитического исследования различных неустановившихся процессов и находит широкое применение при решении многих задач нефтепромысловой механики.

Идея применения операционных методов заключается в том, что при решении задач искомая функция заменяется некоторым преобразованным выражением (изображением) действия над которым проще, чем над самой функцией (оригиналом). Решение задачи получается после нахождения изображения путем обратного перехода к оригиналу. Аналогией может служить идея применения логарифмов в элементарной математике, когда действию например, умножения чисел соответствует более простое действие сложения логарифмов этих чисел. Кроме того, применением операционного метода, как правило, исключается одно из переменных, что намного облегчает решение задачи.

Возможны случаи, когда применением операционного метода обыкновенное дифференциальное уравнение можно свести к алгебраическому.

§ 1. Оригинал и изображение

В основе операционного исчисления лежит преобразование Лапласа.

Пусть имеется функция действительного переменного f (t), кусочно-непрерывная при , равная нулю при. Кроме того, будем считать, что существуют такие числа М > и , что для всех t имеет место неравенство

( s₀ – показатель роста ) т. е. может возрастать с ростом t не быстрее чем . Такую функцию будем называть оригиналом. Перечисленным условиям удовлетворяют почти все функции с которыми приходится сталкиваться при изучении различных физических процессов. Функцию , определяемую равенством

(10.1)

где - комплексная переменная, назовем изображением функции .

Преобразование, сопоставляющее функции изображение , называется преобразованием Лапласа. Тот факт, что является изображением оригинала записывают так:

, или , или .

Пример. Найдем изображение функции

По определению преобразования Лапласа имеем

.

Следовательно, .

Пример. Если в предыдущем примере положить а=0, то получим изображение для функции, которая называется единичной функцией (функцией Хевисайда)

ơ (t) = ׃

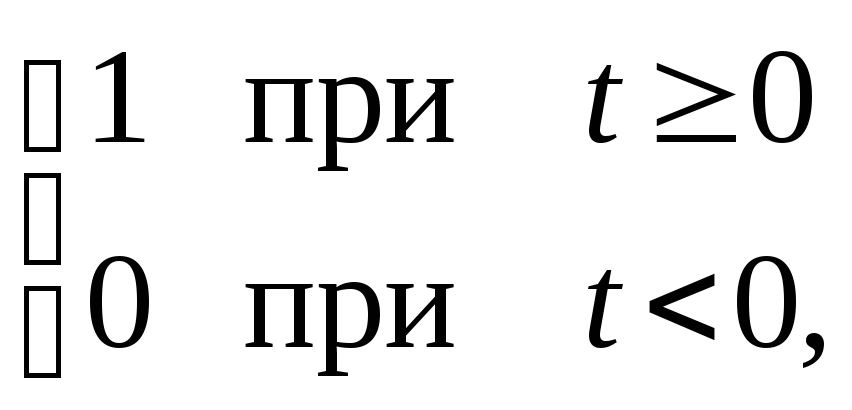
а именно ơ (t)

Из определения изображения (10.1) видно, что для того, чтобы преобразование Лапласа было возможно, необходимо чтобы несобственный интеграл (10.1) существовал для некорой области значений р. Ответ на вопрос о существовании изображения дает теорема:

Для всякого оригинала изображение F (р) определено в полуплоскости причем функция F (р) аналитична в этой полуплоскости.

Доказательство. Пусть — любая точка полуплоскости , тогда, пользуясь определением оригинала, имеем

т. к.

(10.3)

Отсюда вытекает сходимость интеграла, т. е, факт существования изображения F(р) в полуплоскости доказан. Доказательство аналитичности F(р) в полуплоскости , т. е. существования производной в любой точке этой полуплоскости, интересующийся читатель может найти в литературе [1].

Отметим поведение изображения в бесконечно удаленной точке. Из неравенства (10.3) следует, что если так, что при этом , то . Если, в частности, F(р) – аналитическая функция в бесконечно удаленной точке, то при по любому закону, так как .

Итак,

Сформулируем еще теорему единственности оригинала:

Если F(р) служит изображением двух оригиналов и , то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.