§ 3. Изображение функции Дирака
Рассмотрим важную для приложений газонефтепромысловой Механики функцию Дирака.
Определим функцию
график которой представлен на рис. (10.3.)
Эту функцию можно рассматривать как
силу величины
действующую время
,
импульс ее за это время равен 1 при любом
.
Введем
предел
этой функции при
,
который можно считать силой, бесконечно
большой при
и равной нулю для всех t
> 0, но импульс ее по-прежнему равен 1.
Эта функция называется импульсной
функцией нулевого порядка или
-функцией
или функцией Дирака.
Итак,
Изображение
этой функции естественно определить
как предел изображения
при
Имеем
Тогда
.
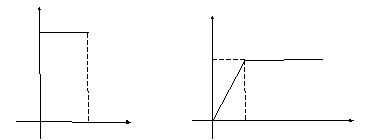
Рис. 10.3 Рис. 10.4
Полученную
функцию
можно считать изображением лишь условно,
так как она не стремится к нулю при
Но для нее имеют место основные теоремы
операционного исчисления. Например,
применяя теорему запаздывания, можно
получить
Рассмотрим
некоторые вопросы, связанные с
-функцией,
важные для приложений.
Обозначим
Очевидно, что
H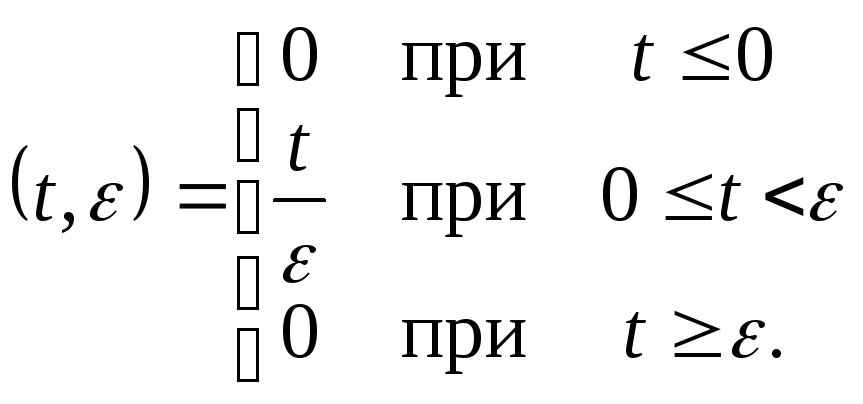
График
функции H
представлен
на рис. (10.4). Кроме того имеем
При
как мы уже видели,
стремится к
-функции.
Для нее справедливо по-прежнему
соотношение
Функция H
при
превращается в единичную функцию
:
=
и
таким образом производная
-функции
равна единичной функции.
Определим интеграл, содержащий импульсную функцию, следующим образом:
.
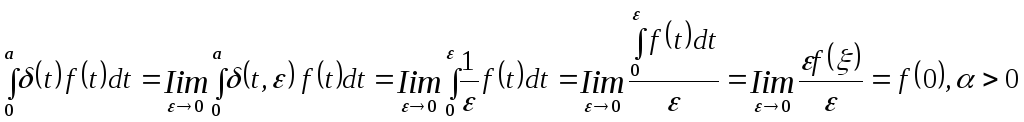Или,
в общем случае при
§ 4. Теорема обращения
Рассмотрим общий случай определения оригинала по известному изображению. Пусть f (t) ← F (p). Будем предполагать, что функцию f (t) можно представить интегралом Фурье, т. е.
По определению изображения
Умножим
обе части последнего равенства на
и проинтегрируем от
до
Тогда получим
В
правой части этого равенства положим
будем иметь
Так
как
при
то
В
этом равенстве перейдем к пределу при
:
Правая
часть последнего равенства представляет
собой интеграл Фурье, с помощью которого
выражается функция
и, следовательно, будем иметь
Отсюда получаем
Эта формула называется формулой обращения. Путь интегрирования выбирается так, чтобы все особенности функции F (р) лежали левее его.
Интеграл (10.8) вычисляется обычно путем перехода к замкнутому контуру и применения теории вычетов.
1.
Пусть функция F
(р)
имеет своими особенностями в плоскости
р
только полюсы. Выберем прямую
так, чтобы все особые точки лежали левее
этой прямой. Тогда интеграл (10.8) вычисляется
на основании леммы Жордана:
Если
F
(р)
стремится к нулю при
,
тогда
где
взятый по дуге
окружности
такой, что на ней
(см. рис.10.5) стремится к нулю при
т.е.
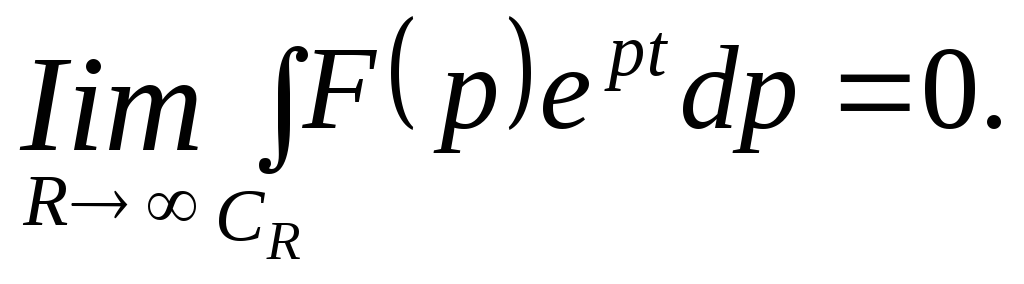
Возьмем
теперь контур, состоящий из отрезка АВ
прямой
и дуги
радиус которой выберем настолько
большим, чтобы все особые точки F
(р)
попали внутрь рассматриваемого контура.
Рис. 10.5
Тогда по теореме о вычетах имеем
На основании леммы Жордана
,
а
интеграл по отрезку АВ,
если
,
переходит в интеграл по прямой
Следовательно, переходя к пределу при
в (10.9), получим
(10.10)
В
частности, если изображение
(является отношением двух целых функций
А
(р)
и В
(р),
т. е. функций, аналитических на всей
комплексной плоскости (
)
и имеющих конечное число нулей, то
особыми точками F
(р)
могут быть только полюсы.
Пользуясь формулой (8.4), для вычисления вычетов на основании (10.10) получаем в случае простых полюсов следующее выражение для оригинала:
2. Если F (р) имеет существенно особые точки и точки ветвления, то в качестве контура интегрирования при вычислении интеграла (10.8) выбирается контур, состоящий из окружностей, заключающих точки разветвления, соединенных разрезами с контуром показанным на рис. (10.5).
Пример.
Найти оригинал изображения
(имеется в виду та ветвь
,
для которой
,
если р >
0).
По формуле обращения
Для вычисления этого интеграла нельзя пользоваться теоремой о вычетах, так как подинтегральная функции многозначна и имеет точку разветвления при р = 0.
Рассмотрим
сначала этот интеграл, взятый по контуру
L,
состоящему из прямой АВ,
дуг окружности ВС,
АF,
малой окружности DЕ
радиуса
,
окружающей начало координат – точку
ветвления, и прямых СD
и FЕ
– разрезов вдоль действительной
оси (рис. 10.б). Внутри контура нет
особых точек, поэтому интересующий нас
интеграл равен 0.
Тогда
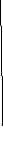
Рис. 10.6
Рассмотрим
интегралы вдоль дуг ВС
и FА
при
Имеем
На
дуге
угол
меняется от
до
,
на дуге
от
до
,
следовательно, на этих дугах
На дуге
угол
меньше
,
а на
больше
,
т. е.
также больше нуля. Поэтому на ВС и FA
будут справедливы неравенства
т.
е.
стремится к нулю при
При этом интегралы по дугам bB и aA стремится к нулю, так как путь интегрирования конечен, а подынтегральная функция стремится к нулю.
Интегралы по дугам bC и Fa стремится к нулю в силу того, что здесь выполняются условия леммы Жордана.
Рассмотрим теперь
Положим
,
на CD
поэтому
Имеем
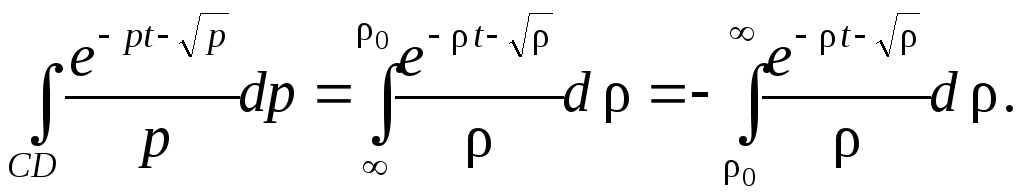
На
поэтому
и
.
Таким образом, искомый интеграл
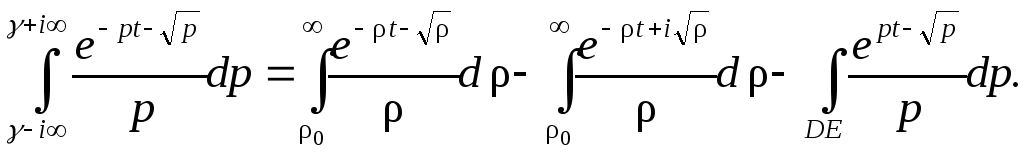
На окружности DE имеем
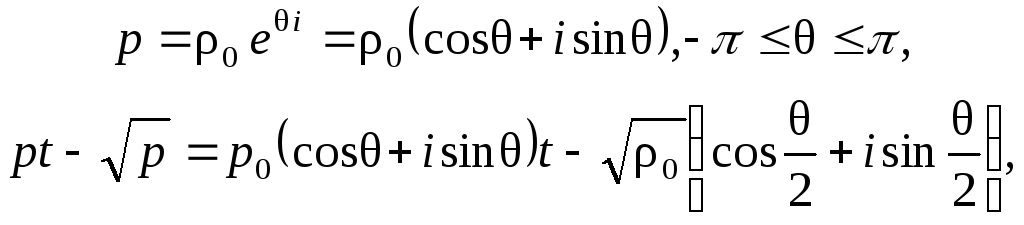
откуда
следует, что на малой окружности DE
величина
имеет порядок малости
,
таким образом
где
при
равномерно относительно
;
учитывая, что
;
получим
где
по модулю меньше, чем
,
т. е. стремится к нулю при
.
Имеем
окончательно при
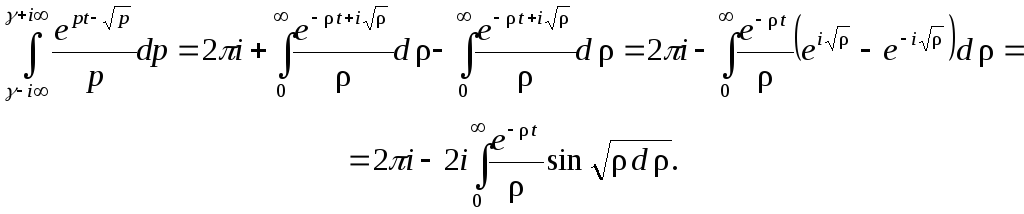
Последний интеграл можно вычислить, используя табличный интеграл
Проинтегрируем его по b в пределах от 0 до b:
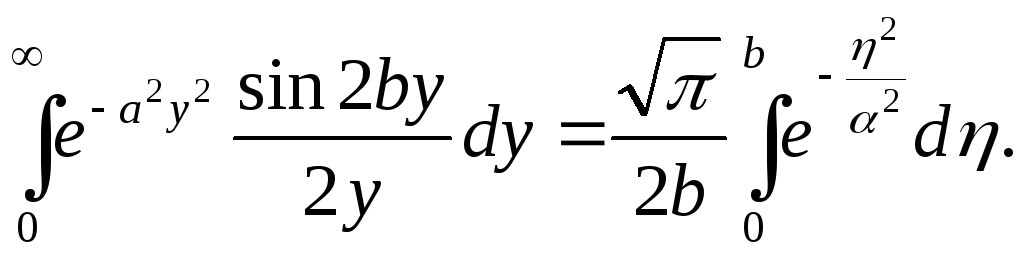
Положим
здесь
получим
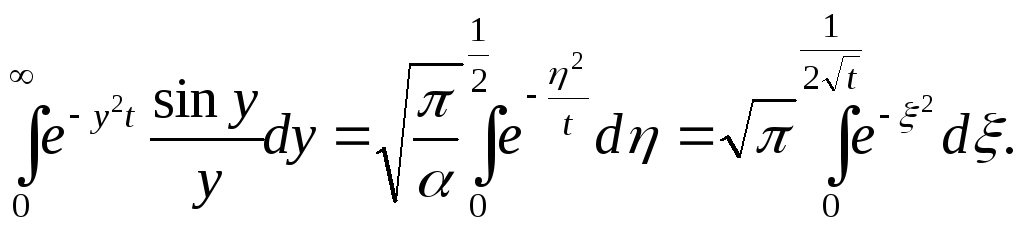
Введя обозначение
можем записать
И так,
