1.3 Эйлеровы графы

Степенью вершины v (обозначается deg v) в графе G называется число ребер, инцидентных вершине v. Граф, каждая вершина v, которого имеет четную степень, называется четным. Эйлеров граф – это связный четный граф.

Пусть W_p – число помеченных четных графов порядка p. Тогда справедлива следующая теорема:

Теорема. Число помеченных четных графов порядка p равно числу помеченных графов порядка p-1:

W_p=.

Доказательство.

Чтобы доказать этот результат, мы сейчас установим взаимно однозначное соответствие между этими двумя графов. Рассмотрим произвольный граф порядка p-1. Граф G должен иметь четное число вершин нечетной степени. Добавим к нему вершину v, которой припишем пометку p. Наконец, из графа G и вершины v строим граф G′, имеющей нечетную степень. Этот граф G′ является помеченным четным графом порядка p. Легко видеть, что описанное соответствие является взаимно однозначным и что каждый помеченный четный граф порядка p может быть получен таким способом из некоторого помеченного графа порядка p-1.

Чтобы получить формулу для числа помеченных эйлеровых графов, мы будем использовать производящие функции. Итак, пусть W(t) – экспоненциальная производящая функция для помеченных четных графов, такая что

W(t) =t^p/p! (10)

Далее, пусть U_p – число помеченных эйлеровых графов порядка p, так что

U(t) =t^p/p! (11)

является соответствующей экспоненциальной производящей функцией.

Теорема. Экспоненциальная производящая функция U(t) для помеченных эйлеровых графов удовлетворяет соотношениям

U(t) =ln(W(t)+1) (12)

и

U_p= -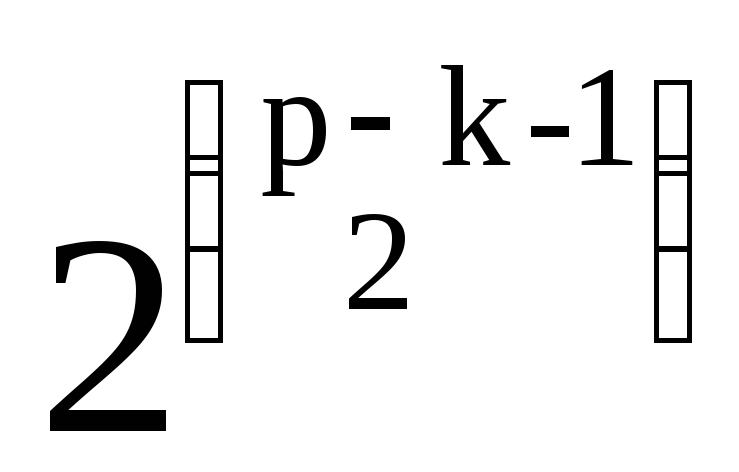U_k. (13)

Формула (12) следует из того факта, упомянутого после равенства (8), что если известна производящая функция для произвольного класса графов, то производящая функция для соответствующих связных графов получается с помощью формального логарифмирования первого ряда. Рекуррентное соотношение (13) для U_p является следствием формул (12) и (9).

Для нескольких первых членов ряда U(t) имеем равенство

U(t)=t+t³/3!+ 3t⁴/4!+ 38t⁵/5!+… (14)

Упражнение. Проверьте справедливость равенства (14).

К несколько более трудной относится задача – определение числа помеченных эйлеровых графов с заданным числом вершин и ребер, установленный Ридом.

Теорема⁷. Многочлен w_p(t), у которого коэффициент при t^q равен числу помеченных графов имеющих p вершин четной степени и q ребер, задается формулой

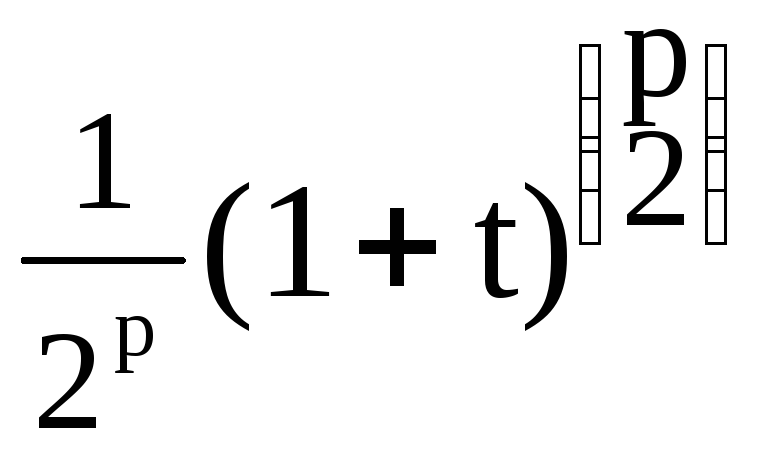
w_p(t)= . (15)

Для малых значений p находим, что (проверьте):

W₁(t)= w₂(t)=1 w₃(t)=1+t³ w₄(t)=1+4t³+ 3t⁴.

1.7 Деревья

Деревом называется связный граф, не имеющий циклов. Известно, что всякое нетривиальное дерево имеет не менее двух висящих вершин (вершины степени 1). Это Следует из того, что если T – дерево с p вершинами и q ребрами, то

q=p-1.

Теорема.(Кэли 1897). Число _p помеченных деревьев порядка p равно

_p=p^p-2.

Доказательство.

Первый подход (Кэли) Установим соответствие между помеченными деревьями и функциями, отображающими множество из p-2 объектов в множество из p объектов. Например, если p=5, то существует 5³ функций из {a,b,c} в {v₁, v₂, v₃, v₄, v₅}. Эти функции перечисляются многочленом

(v₁+ v₂+ v₃+ v₄+ v₅)³. (16)

Слагаемые этого многочлена сопоставляются функциям естественным образом. Например, соответствует постоянной функции f(x)=v₄, слагаемое отвечает трем функциям, которые отображают только один элемент в v₁, два других – в v₃, 6v₂v₃v₅ дает шесть функций, отображающих по одному элементу в v₂, v₃ и v₅. Теперь, умножая многочлен на v₁v₂v₃v₄v₅ и получая

(v₁+ v₂+ v₃+ v₄+ v₅)³ v₁v₂v₃v₄v₅ (17)

устанавливаем тем самым соответствие между слагаемыми из этого произведения и помеченными деревьями порядка 5. Это соответствие с использованием слагаемого=v₁v₂v₃v₄v₅) выглядит так

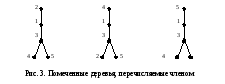
Заметим, что в деревьях, соответствующих слагаемому , степень вершины, помеченной числом k, равна показателю степени у v_k. Справедливость этого высказывания может быть установлена и в общем случае. Следовательно, число помеченных деревьев, у которых вершины, помеченные числом k, имеют степень d_k, равно полиномиальному коэффициенту

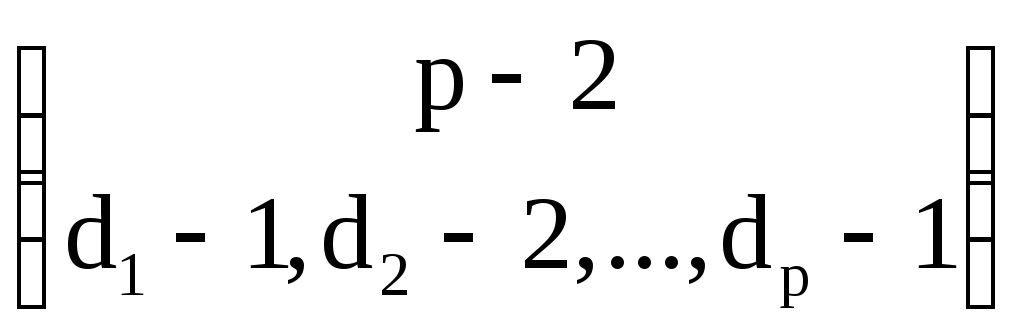. (18)

Кэли проиллюстрировал это соответствие для p=6 и не стал рассатривать другие случаи, заметив: “Сразу видно, что доказательство, данное для этого частного случая, применимо при любом значении p”.

Второй подход (Прюфер 1917). Пусть дерево с n вершинами, помеченными числами 1, …,n. Свяжем с этим деревом последовательность натуральных чисел i₁,…,i_n-2 , построенную следующим образом:

1)положим j=0;

2)повторим следующий процесс n-2 раза:

увеличим значение j на единицу; найдем в дереве лист, помеченный натуральным числом с наименьшим значением. Пусть это значение k_j, и пусть отцом листа k_j является вершина, помеченная числом i_j. Выберем значение i_j в качестве j-ого элемента последовательности. Удалим в дереве ребро (i_j,k_j).

После исполнения этого алгоритма начальное дерево преобразуется в дерево, состоящее из одного ребра либо (i_n-2,n), либо, в случае i_n-2=n, – из ребра (n,n-1).