Санкт-Петербургский государственный
университет
Математико-механический факультет
В. А. Костин
Конкретная математика (Лекции 2004, фрагменты)
Санкт-Петербург
2004
09.05.2004
Докажем, что число счастливых 2n-значных трамвайных билетов равно
.
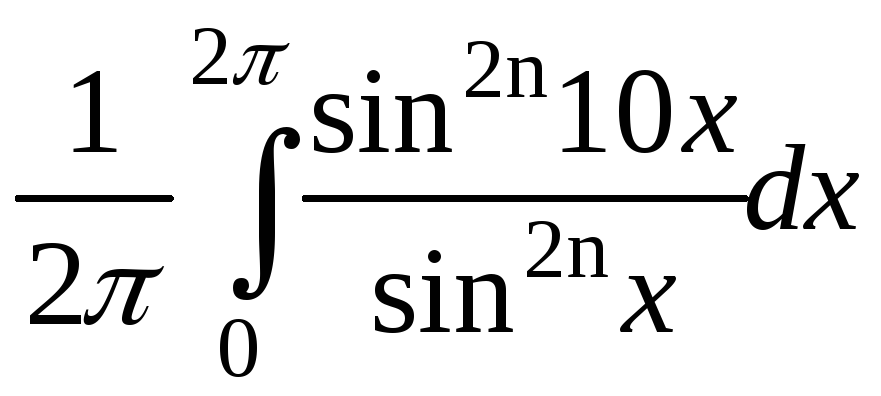Билет считается счастливым, если сумма первых n цифр его номера равна сумме n последних цифр, например, билет с номером 764395 – счастливый шестизначный билет.
Упражнение. Докажите, что функция от параметра n, вычисляющая число счастливых 2n-значных трамвайных билетов, примитивно рекурсивна.
Доказательство (леммы).
Рассмотрим
равенство (1+z+…+z9)n=
,
тогда аi определяет количество
n-значных чисел, сумма цифр которых равна
i.
Нам нужно
вычислить
.
Имеем
(1+z+…+z9)n(1+z-1+…+z-9)n=
=
,
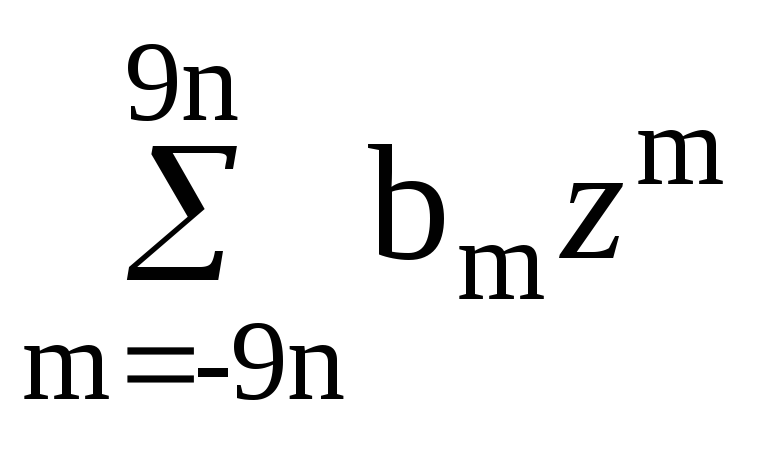тогда
b0=
.
(1+z+…+z9)n(1+z-1+…+z-9)n=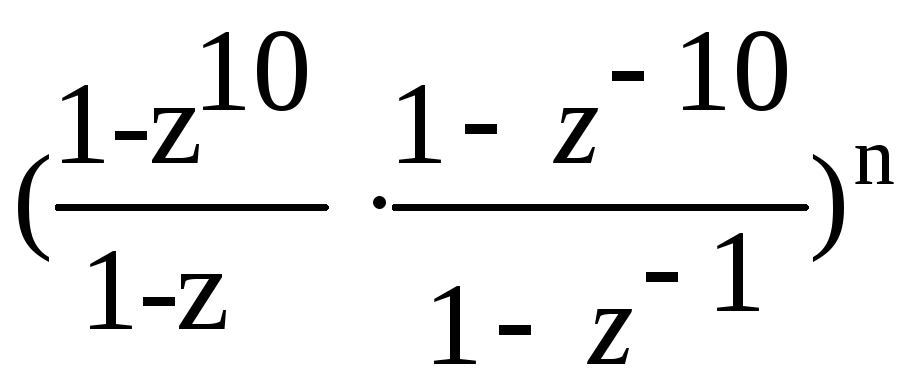
=
.
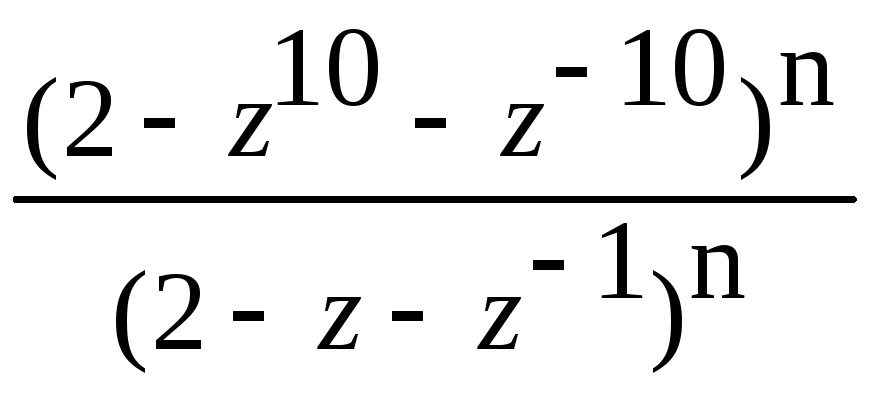Известно,
что
=
.
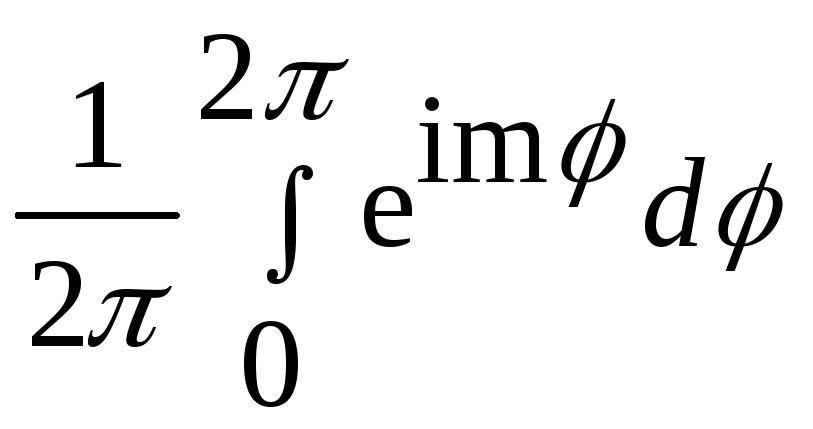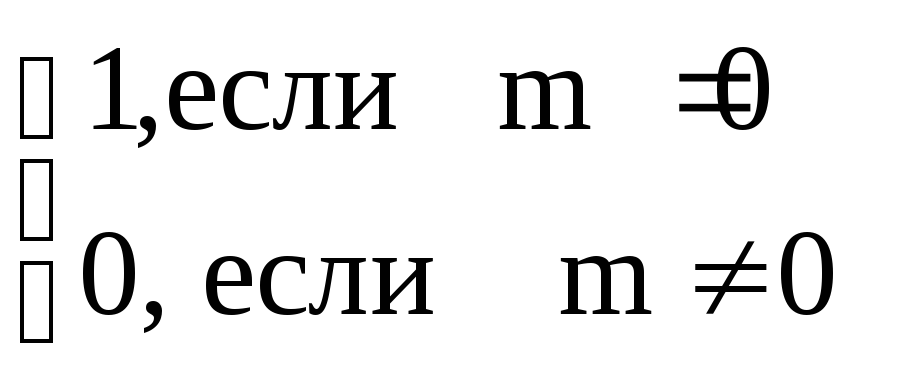Пусть
z=ei=cos+isin,
тогда b0=
=
=
.
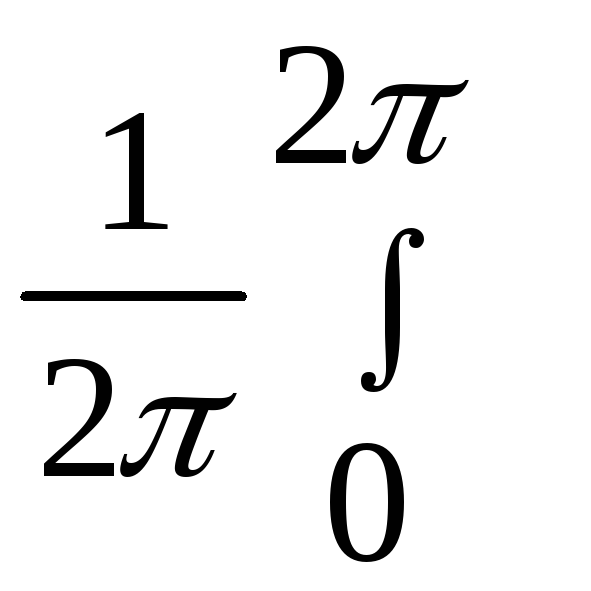
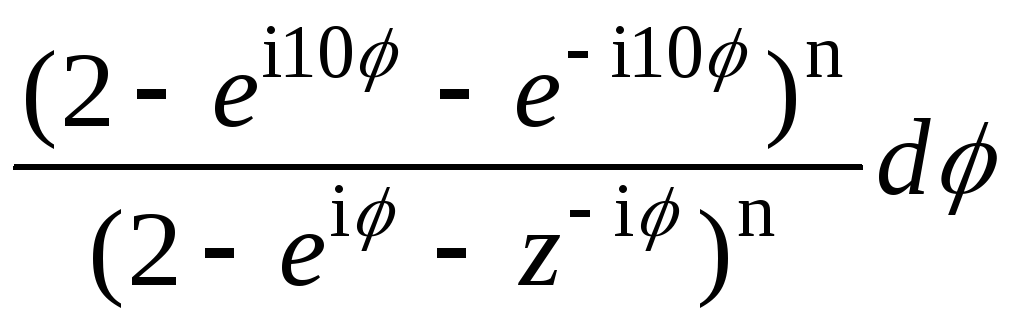Преобразуем
=
=
=
=
.
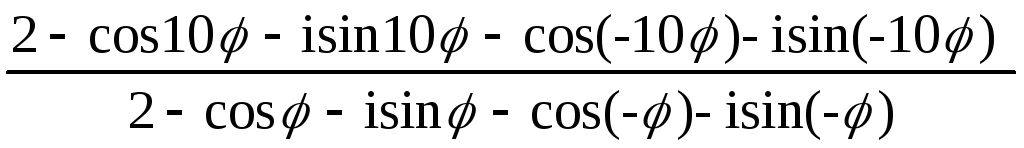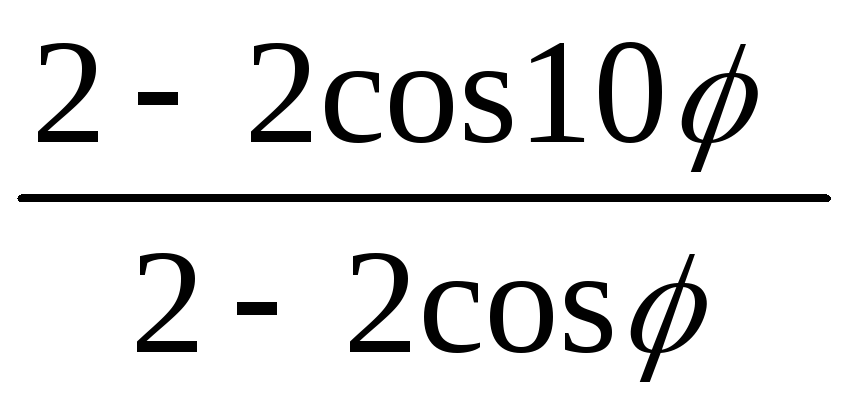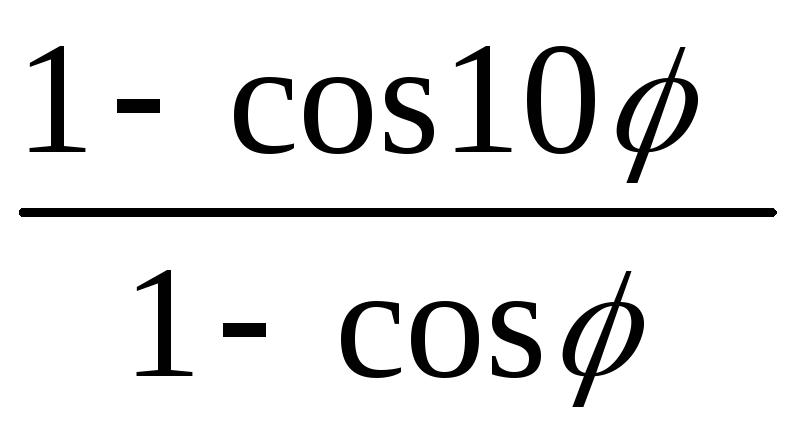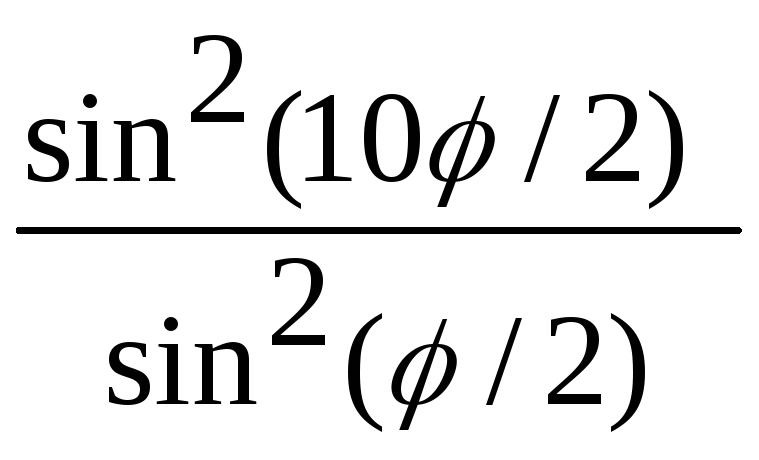Таким образом,
b0=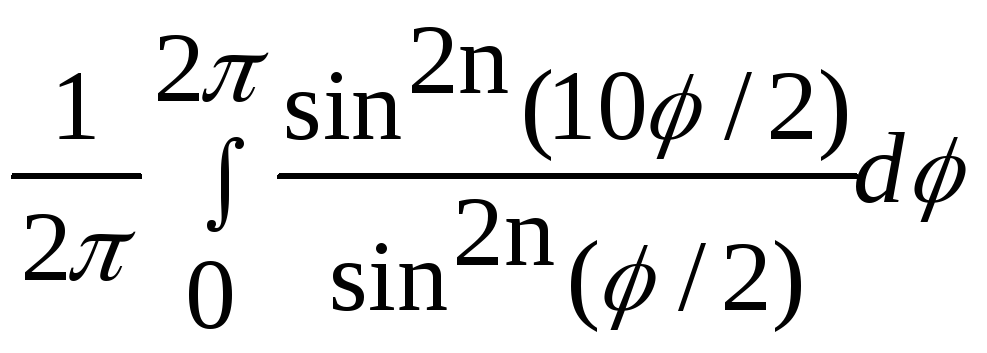
=
=
.
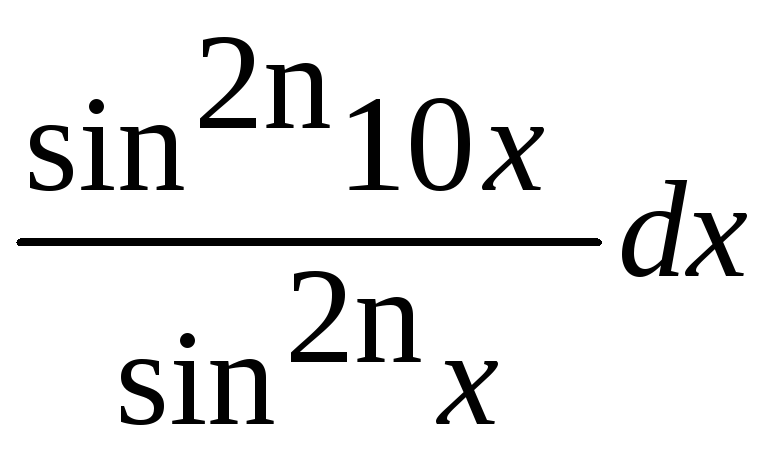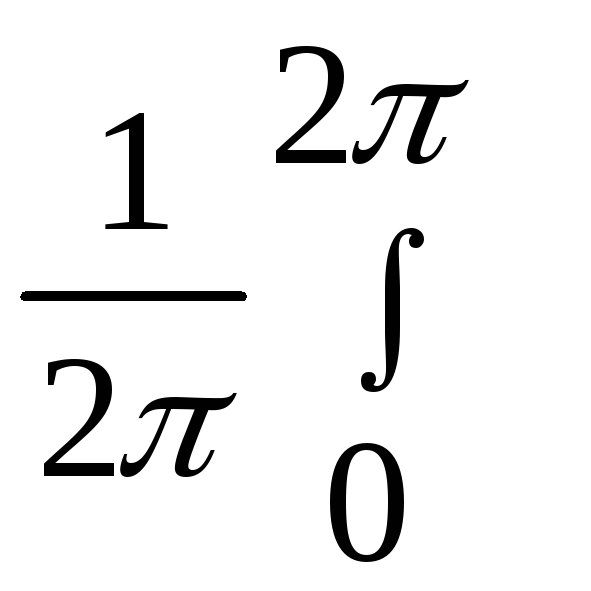
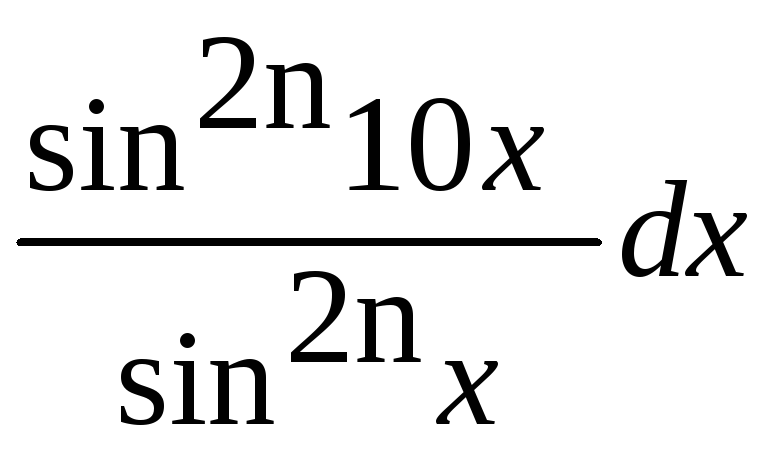При доказательстве тех или иных комбинаторных тождеств часто используется одно или одновременно два из следующих правил:
Правило суммы. Если объект А может быть выбран m способами, а объект В другими n способами, то выбор “либо А, либо В” может быть осуществлен m+n способами.
Правило произведения. Если объект А может быть выбран m способами и после каждого из таких выборов объект В в свою очередь может быть выбран n способами, то выбор “А, и В” в указанном порядке может быть осуществлен mn способами.
Примеры.
На основе этих правил в курсе математического
анализа легко были получены формулы
для числа k-перестановок
и числа k-сочетаний
из n
объектов, а именно
=
n(n-1)…(n-k+1)
=
Упражнение. Докажите, что число k-перестановок из n объектов с повторениями равно nk.
Задача.
Доказать, что число k-сочетаний
из n
объектов с повторениями равно
.
Решение (Л. Эйлер): Пусть X={1,2,…n} и рассмотрим любое из k-сочетаний с повторениями с1с2…сk этих n чисел (считаем, что в сочетании с1с2…сk элементы выписаны в неубывающем порядке). Естественно, что в каждом сочетании вследствие возможности неограниченных повторений любые рядом стоящие элементы могут быть одинаковыми. Ввиду этого обстоятельства строим с помощью соотношений
d1=c1+0; d2=c2+1;…; di=ci+i-1;…; dk=ck+k-1
последовательность
элементов d1d2…dk
следовательно, при любых элементах ci
элементы di
всегда различны. Ясно, что отображение
с1с2…сk
в d1d2…dk
биективно. Число последовательностей
из элементов di
равно числу k-сочетаний
без повторений из элементов от 1 до
n+k-1,
т. е.
.
Производящие функции для сочетаний.
Для примера рассмотрим три объекта, обозначенные x1, x2, x3. Образуем произведение
(1+x1t)(1+ x2t)(1+x3t).
Перемножив и разложив это произведение по степеням t, получим
1+(x1+x2+x3)t+(x1x2+x1x3+x2x3)t2+x1x2x3t3,
или
1+а1t+а2t2+а3t3,
где а1, а2, а3 – элементарные симметрические функции трех переменных x1, x2, x3. Эти симметрические функции определяются вышеприведенным выражением. Можно заметить, что число слагаемых каждого коэффициента аm (m=1,2,3) равно числу сочетаний из трех элементов по k. Следовательно, число таких сочетаний получается приравниванием каждого xi единице, т. е.
(1+t)3=
Для случая n различных объектов, обозначенных x1, . . . , xn ясно, что
(1+x1t)(1+ x2t) . . . .(1+xnt)=
=1+a1(x1,. . ., xn)t+ a2(x1,. . ., xn)t2+. . .+ an(x1,. . ., xn)tn
и
(1+t)n=
=
;
поэтому выражение (1+t)n называют перечисляющей функцией сочетаний из n различных объектов. Этот результат можно также обосновать следующими комбинаторными рассуждениями:
В произведении (1+x1t)(1+ x2t) . . . .(1+xnt) каждый множитель является биномом, который благодаря наличию в нем слагаемых 1 и xi указывает на возможность наличия или отсутствия в каждом из сочетаний элемента xi. Это произведение порождает сочетания, так как коэффициент при tm в нем получается выбором “1” в n-m из n двучленных множителей и в m оставшихся после такого выбора множителях - членов вида xit всеми возможными путями. Эти коэффициенты по самому их определению являются m-сочетаниями. Каждый элемент в любом сочетании может появляться не более одного раза, ибо любой множитель состоит только из двух слагаемых.
Обобщая
эти комбинаторные рассуждения, для
случая, когда прежние множители вида
1+xit
заменяются множителями вида 1+x
t+x
t2+
… +x
tj,
построим производящую функцию для
сочетаний, в которых элементы xi
могут содержаться 0,1,2,…,j
раз. Более того, множители производящей
функции можно совершенно независимо
друг от друга приспосабливать к любым
требованиям задачи. Так, например, если
xk
должно всегда входить четное число раз,
но не более чем 2k
раз, то k-й
множитель следует выбирать в виде
1+x
t+x
t4+
… +x
t2k
.
Таким образом, производящая функция для любой задачи описывает не только виды элементов, но и виды искомых сочетаний.
Пример. Для сочетаний с неограниченным повторением элементов n и без ограничения на число появлений любого элемента перечисляющей производящей функцией будет
(1+t+t2+. . .)n
или, что же самое
(1-t)-n
=
=
=
.
Упражнение. 1. Постройте производящую функцию для сочетаний с повторениями, в которых каждый элемент входит, по крайней мере, один раз.
2. Постройте производящую функцию для сочетаний с повторениями, в которых любой элемент обязательно появляется в сочетании, но только четное число раз.